高中数学苏教版 (2019)必修 第一册第3章 不等式3.1 不等式的基本性质优秀课后练习题

这是一份高中数学苏教版 (2019)必修 第一册第3章 不等式3.1 不等式的基本性质优秀课后练习题，共28页。
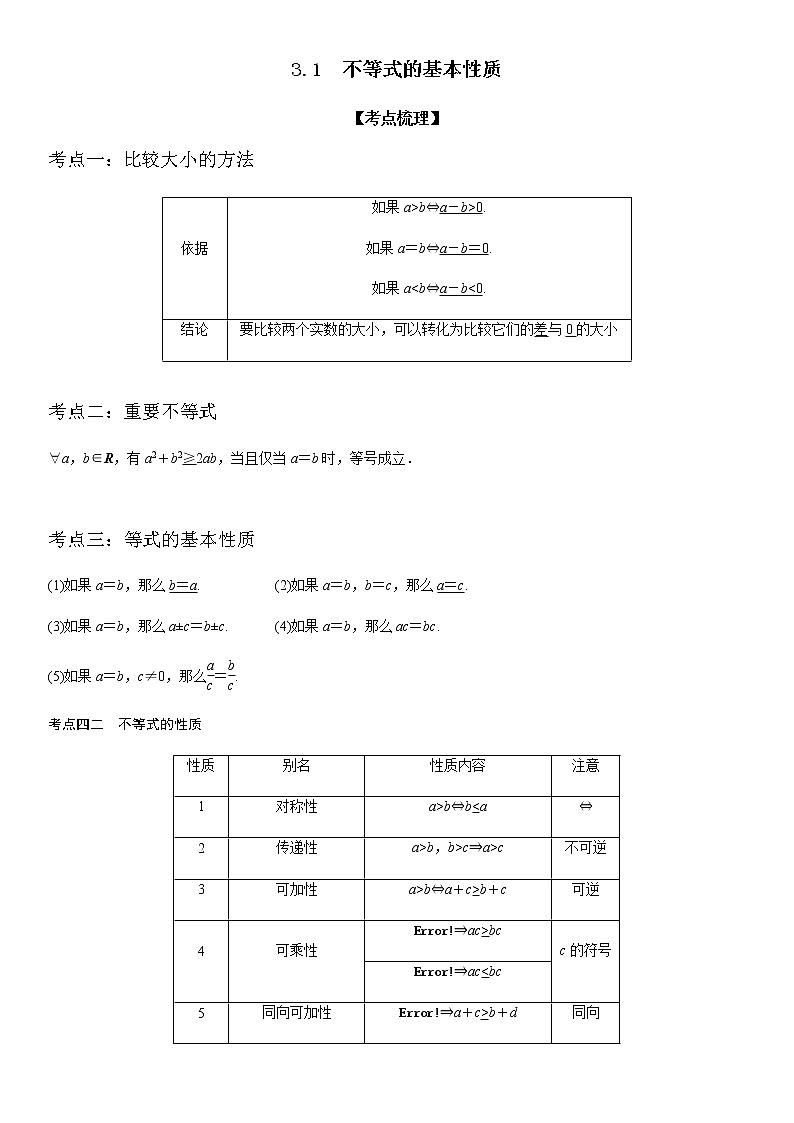
3.1　不等式的基本性质【考点梳理】考点一：比较大小的方法依据如果a>b⇔a－b>0. 如果a＝b⇔a－b＝0. 如果a<b⇔a－b<0.结论要比较两个实数的大小，可以转化为比较它们的差与0的大小 考点二：重要不等式∀a，b∈R，有a2＋b2≥2ab，当且仅当a＝b时，等号成立． 考点三：等式的基本性质(1)如果a＝b，那么b＝a. (2)如果a＝b，b＝c，那么a＝c.(3)如果a＝b，那么a±c＝b±c. (4)如果a＝b，那么ac＝bc.(5)如果a＝b，c≠0，那么＝.考点四二　不等式的性质性质别名性质内容注意1对称性a>b⇔b<a⇔2传递性a>b，b>c⇒a>c不可逆3可加性a>b⇔a＋c>b＋c可逆4可乘性⇒ac>bcc的符号⇒ac<bc5同向可加性⇒a＋c>b＋d同向6同向同正可乘性⇒ac>bd同向7可乘方性a>b>0⇒an>bn(n∈N，n≥2)同正    【题型归纳】题型一：已知条件判断所给不等式的大小1．（2022·陕西·扶风县法门高中高一阶段练习）下列结论正确的是（    ）A．若，则 B．若，则C．若，，则 D．若，则2．（2022·江苏·南京市中华中学高一阶段练习）下列结论正确的是（    ）A．若，则 B．若，则C．若，则 D．若，则3．（2022·广东·东莞市海德实验学校高一阶段练习）已知均为实数，则下列命题中错误的是（　　）A．若，，则B．若，，则C．若，，则D．若，则 题型二：不等式的性质比较数的大小4．（2022·全国·高一单元测试）已知，则下列大小关系正确的是（    ）A． B．C． D．5．（2022·北京平谷·高一期末）已知a，b，，那么下列命题中正确的是（    ）A．若，则 B．若，则C．若，，则 D．若，，则6．（2022·全国·高一课时练习）已知，则的大小关系为（    ）A． B．C． D．  题型三：作差法或作商法比较不等式的大小7．（2022·河南省叶县高级中学高一阶段练习）若，则下列不等式一定成立的是（    ）A． B．C． D．8．（2022·全国·高一课时练习）设a＞b＞1，y1，则y1，y2，y3的大小关系是（    ）A．y1＜y2＜y3 B．y2＜y1＜y3 C．y3＜y2＜y1 D．y2＜y3＜y19．（2021·山东·泰安一中高一期中）设，，则（    ）．A． B． C． D． 题型四：利用不等式求取值范围10．（2022·江苏省如皋中学高一阶段练习）已知实数，满足，，则的取值范围是（    ）A． B．C． D．11．（2021·全国·高一期中）已知实数满足，，则的取值范围是（      ）A． B．C． D．12．（2021·山东·临沂第二中学高一阶段练习）若，，则的取值范围为（       ）A． B．C． D． 题型五：由不等式性质证明不等式13．（2021·全国·高一专题练习）（1）若bc－ad≥0，bd>0，求证：≤；（2）已知c>a>b>0，求证：  14．（2021·黑龙江·尚志市尚志中学高一阶段练习）已知，，（1）.求证：；（2）若，求证：；  15．（2022·全国·高一专题）（1）若，，求证：；（2），，，求证：  【双基达标】一、单选题16．（2022·广东·东莞市海德实验学校高一阶段练习）已知﹣1＜a+b＜3，且2＜a﹣b＜4，那么的取值范围是（     ）A． B．C． D．17．（2022·河南·中学生学习报附中高一阶段练习）已知，，则M，N的大小关系是（    ）A． B． C． D．18．（2022·陕西·扶风县法门高中高一阶段练习）“”是“”的（    ）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件19．（2022·广东·东莞实验中学高一阶段练习）下列命题中，是真命题的是（    ）A．如果，那么 B．如果，那么C．如果，那么 D．如果，那么20．（2022·湖南·衡阳市第六中学高一开学考试）已知是关于的不等式的一个解，则的取值范围为（    ）A． B． C． D．   21．（2022·山东·惠民县第二中学高一阶段练习）如果，则正确的是（    ）A．若a>b，则 B．若a>b，则C．若a>b，c>d，则a+c>b+d D．若a>b，c>d，则ac>bd 【高分突破】一、单选题22．（2022·全国·高一课时练习）下列命题正确的是（    ）A． B．C．且 D．23．（2022·全国·高一专题练习）已知，且，则以下不正确的是（    ）A． B． C． D．24．（2022·湖南·新化县教育科学研究所高一期末）已知a，b，c，d均为实数，则下列命题正确的是（    ）A．若，，则B．若，，则C．若，则D．若，则25．（2022·山西吕梁·高一期末）已知，则（    ）A． B．C． D．的取值范围是二、多选题26．（2022·吉林·东北师大附中高一阶段练习）实数，，，满足：，则下列不等式正确的是（    ）A． B． C． D．27．（2022·宁夏·银川二中高一阶段练习）下列说法正确的是（    ）A．若，，则 B．若，则C．若，则 D．若，则   28．（2022·河北·青龙满族自治县实验中学高一阶段练习）若、、，，则下列不等式不正确的是（    ）A． B．C． D．29．（2022·湖北·沙市中学高一阶段练习）已知均为实数，下列命题正确的是（    ）A．已知，则存在负数使成立B．“”是“”的充分不必要条件C．若，，，则D．若正数满足，则30．（2022·江苏省如皋中学高一开学考试）已知，下列命题为真命题的是(    )A．若，则 B．若，则C．若，则 D．若，则31．（2022·湖北·恩施土家族苗族高中高一阶段练习）2022年1月，在世界田联公布的2022赛季首期各项世界排名中，我国一运动员以1325分排名男子100米世界第八名，极大地激励了学生对百米赛跑的热爱．甲、乙、丙三名学生同时参加了一次百米赛跑，所用时间（单位：秒）分别为，，．甲有一半的时间以速度（单位：米/秒）奔跑，另一半的时间以速度奔跑；乙全程以速度奔跑；丙有一半的路程以速度奔跑，另一半的路程以速度奔跑．其中，．则下列结论中一定成立的是（    ）A． B．C． D． 三、填空题32．（2022·河南·禹州市高级中学高一阶段练习）若，，则的取值范围为______．33．（2022·江苏·高一单元测试）已知，，则，的大小关系是________．34．（2022·上海·高一单元测试），，则的最小值是___________.35．（2022·全国·高一课时练习）已知，则的值______0（选填“>，<，≥，≤”）．  36．（2022·上海·高一单元测试）已知，下列命题中正确的是______(将正确命题的序号填在横线上)①若，则      ②若，则;③若，则;        ④若，则.37．（2022·全国·高一）若a、b∈R，则下列不等式：①a2＋3＞2a；②a2＋b2≥2(a－b－1)；③a5＋b5＞a3b2＋a2b3；④a＋≥2中一定成立的是__________．(填序号) 四、解答题38．（2022·河南省叶县高级中学高一）求解下列问题：(1)已知，比较和的大小；(2)已知，比较与的大小. 39．（2022·江苏·南京市中华中学高一）已知，.(1)分别求a，c的取值范围；(2)求的取值范围. 40．（2022·全国·高一）（1）已知，求证：；（2）已知，且，比较与的大小． 41．（2022·全国·高一）试比较下列组式子的大小：(1)与，其中；(2)与，其中，；(3)与，． 42．（2021·上海市洋泾中学高一）设是四个正数．(1)已知，比较与的大小；(2)已知，求证：中至少有一个小于1．
参考答案：1．C【分析】利用特殊值排除错误选项，利用差比较法证明正确选项.【详解】A选项，，如，而，所以A选项错误.B选项，，如，而，所以B选项错误.C选项，，则，所以，所以C选项正确.D选项，，如，而，所以D选项错误.故选：C2．C【分析】根据不等式的性质即可逐一求解.【详解】对于A;若，时，则，故A错；对于B;若取，则无意义，故B错；对于C；根据不等式的可加性可知：若，则，故C正确；对于D;若取，但,故D错；故选：C3．A【分析】，即可判断ABC，由可得，然后可判断D.【详解】对于A，因为，，所以，故A错误；对于B，因为，，所以，故B正确；对于C，因为，，所以，故C正确；对于D，由可得，所以，故D正确，故选：A4．C【分析】结合不等式的性质以及差比较法确定正确答案.【详解】为正数，为负数，所以，，，所以.故选：C5．C【分析】根据不等式的性质或通过举反例，对四个选项进行分析．【详解】．若，当时， ，所以不成立；．若，当时，则，所以不成立；．因为，将两边同除以，则，所以成立．若且，当时，则，所以，则不成立．故选：．6．C【分析】由不等式的基本性质可得答案.【详解】由，有，可得.故选：C7．C【分析】对A，B，C，D选项作差与0比较即可得出答案.【详解】对于A，因为，故，即，故A错误；对于B，，无法判断，故B错误；对于C，因为，，故C正确；对于D，因为，故，即，故D错误．故选：C．8．C【分析】利用作差法先比较y1，y2，再比较y2，y3即可得出y1，y2，y3的大小关系.【详解】解：由a＞b＞1，有y1﹣y20，即y1＞y2，由a＞b＞1，有y2﹣y30，即y2＞y3，所以y1＞y2＞y3，故选：C.9．D【分析】首先配方判断、均大于零，然后作商即可比较大小.【详解】，，则.故，当且仅当时，取等号，故选：D【点睛】本题考查了作商法比较两个式子的大小，属于基础题.10．B【分析】令，，可得，再根据的范围求解即可.【详解】令，，则，所以．因为，所以．因为，所以，所以.故选：B11．B【分析】令求出，再由不等式的性质求解即可.【详解】令，即故，解得因为，，所以故选：B12．B【分析】利用不等式的基本性质即可得出．【详解】解：因为，，所以，所以，故选：B13．（1）证明见解析；（2）证明见解析.【分析】（1）由不等式的性质，先得到，两边同时+1，即得证；（2）由不等式的性质，先得到，两边乘以c,可得，两边同时-1，可得，再两边取倒数，即得证.【详解】证明：（1）∵bc≥ad，bd>0，∴，∴＋1≥＋1，∴≤.（2）∵c>a>b>0，∴c－a>0，c－b>0.∵a>b>0，∴又∵c>0，∴，∴，又c－a>0，c－b>0，∴.14．（1）证明见解析；（2）证明见解析.【分析】（1）利用作差法可求两者的大小关系.（1）利用（1）的结果可证明不等式成立.【详解】证明：（1）∵∴；（2）由（1）得，故，而，所以.15．（1）证明见解析，（2）证明见解析【分析】（1）利用作差法证明即可，（2）利用不等式的性质证明即可【详解】（1）因为，，所以，所以（2）因为，所以，因为，所以，所以，所以，所以，因为，所以，即16．A【分析】令，列方程组可得，根据不等式的性质及题干条件，即得解【详解】由题意，故，解得由﹣1＜a+b＜3，可得；由2＜a﹣b＜4，可得；故故选：A17．A【分析】用作差法比较大小．【详解】，所以．故选：A．18．C【分析】利用作差法、不等式的基本性质结合充分条件、必要条件的定义判断可得出结论.【详解】由可得，由已知且，若，则，所以，，则，矛盾.若，则，从而，合乎题意.综上所述，“”是“”的充要条件.故选：C.19．B【分析】根据不等式的性质和特殊值法，逐项验证可得出答案【详解】解：对于A，如果，，那么，故A错误；对于B，易得，所以，所以化简得，故B正确；对于C，如果，，那么，故C错误；对于D，因为满足，那么，故D错误；故选：B20．B【分析】把“x=3”代入不等式即可解得.【详解】将“x=3”代入不等式可得，解得：.故选：B21．C【分析】根据不等式的性质即可逐一求解.【详解】对于A:取则，故A错，对于B:若，则，故B错误，对于C:由同号可加性可知：a>b，c>d，则a+c>b+d，故C正确，对于D:若，则，，故D错误.故选：C22．A【分析】根据不等式的性质逐一判断即可【详解】对于选项A，∵，∴，又， 成立，故A正确；对于选项B，当，时，结论明显错误，故B错误对于选项C，当时，，所以结论错误，故C错误对于选项D，当时，，所以结论错误，故D错误故选：A23．D【分析】利用不等式的性质，逐一分析即可得出答案.【详解】，，，故A，B正确；，即，故C正确；对两边同除得，故D错误.故选：D.24．B【分析】利用不等式的性质逐项判断可得出合适的选项.【详解】对于A选项，若，，则，故，A错；对于B选项，若，，则，所以，，故，B对；对于C选项，若，则，则，C错；对于D选项，若，则，所以，，D错.故选：B.25．B【分析】取判断A；由不等式的性质判断BC；由基本不等式判断D.【详解】当时，不成立，A错误．因为，所以，，B正确，C错误．当，时，，当且仅当时，等号成立，而，D错误．故选：B26．ACD【分析】利用不等式的性质判断A、C，利用特殊值判断B，再利用作差法判断D；【详解】解：因为，所以，故A正确；令、、、，满足，此时，故B错误；因为，所以，，所以，故C正确；因为，则，因为，，所以，即，故D正确；故选：ACD27．BC【分析】取，，可判断A；当，可得，由，利用不等式的基本性质可判断B；当时，利用不等式的基本性质可判断C；取，可判断D.【详解】解析：若，，时，不成立，A错误；因为，当，时，，故，，B正确；因为，当时，，故，因为，当时，，故所以C正确；若，，不满足，D错误．故选：BC.28．ABC【分析】利用不等式的性质即可判断.【详解】对于A，由，则，则，即，故A不正确；对于B，由，则，故B错误；对于C，当时，，当时，，故C不正确；对于D，由，，所以，故D正确.故选：ABC.29．AC【分析】A、C、D利用作差法转化为商或积的形式，结合已知条件、不等式性质判断正误；B令结合充分性定义即可判断正误.【详解】A：，而，若为负数，则，当时，此时成立，正确；B：当时，的大小不确定，即“”不能推出“”，充分性不成立，错误；C：，而，，，则，故，，故，即，正确；D：，故时，原不等式也成立，错误.故选：AC30．BCD【分析】根据不等式的基本性质逐项判断即可．【详解】对于选项A，若，则，故A错误；对于选项B，若，∵，∴，故B正确；对于选项C，若，则，故，故C正确；对于选项D，若，则，故D正确．故选：BCD．31．AC【分析】首先利用时间和速度的关系表示三人的时间，再利用不等式的关系，结合选项，比较大小，即可判断选项.【详解】由题意，所以，，，根据基本不等式可知，故，当且仅当时等号全部成立，故A选项正确，B选项错误；，故C选项正确；，故D选项错误．故选：AC．32．．【分析】结合不等式的性质，按的正负分类讨论．【详解】，若，则，若，则，，所以，综上．故答案为：．33．【分析】利用作差法直接比大小.【详解】,故答案为：.34．##【分析】分析可得，利用不等式的基本性质可求得的最小值.【详解】设，则，解得，所以，，因此，的最小值是.故答案为：.35．≤【分析】先平方，整理可得，结合的符号可得答案.【详解】因为，所以，所以.当时，等号成立故答案为：36．②③【分析】①取检验即可；②和③利用不等式两端同时乘以一个正数，不等式的方向不改变；④取检验即可【详解】①若，当时，则，故①错误；②若，不等式两边同时乘以，则，故②正确；③若，不等式两边同时乘以，则，故③正确；④若，当时，则，故④错误；故答案为：②③37．①②【分析】利用作差法及不等式性质，即可作出判断.【详解】①a2－2a＋3＝(a－1)2＋2＞0，正确；②a2＋b2－2a＋2b＋2＝(a－1)2＋(b＋1)2≥0，正确；③a5－a3b2＋b5－a2b3＝a3(a2－b2)＋b3(b2－a2)＝(a2－b2)(a3－b3)＝(a＋b)(a－b)2(a2＋ab＋b2)，若a＝b，则上式＝0，不正确；④若a＜0，则a＋＜0不正确.∴①②一定成立.故答案为：①②38．(1)(2) 【分析】（1）用作差法比较大小；（2）用作差法比较大小．（1）－．所以；（2）∵，∴，，∴，所以．39．(1)，；(2)． 【分析】（1）设，，即得，，根据不等式的性质即可求出，的取值范围；（2）由（1）可知，，即可根据不等式的性质求出取值范围．（1）设，，则，，，，由，则，，则的取值范围是，的取值范围是；（2），由，，则，，则.40．（1）证明见解析；（2）答案见解析.【分析】（1）作差后变形化简证明即可；（2）利用作差法，分类讨论证明即可.【详解】（1) ，因为，所以， ，所以，故 .(2) ．由于，所以当时，，即；当时， ，即．41．(1); (2); (3). 【分析】(1)通过比较与的大小来确定与的大小；(2)通过作差法来比较的大小；(3) 通过作差法或作商法比较与的大小.（1）解：，，因为，所以，即；（2）解：．因为，，所以，，所以，即；（3）方法一（作差法）．因为，所以，，，．所以，所以．方法二（作商法） 因为，所以，，，所以，所以．42．(1)(2)证明见解析 【分析】(1)利用比差法比较与的大小；(2)利用反证法证明.（1）因为是四个正数，，所以，所以，因为，所以，因为是四个正数，所以，所以所以（2）假设都不小于1，则，那么与已知条件矛盾，所以假设不成立，所以中至少有一个小于1．