人教B版 (2019)必修 第二册5.3.4 频率与概率多媒体教学ppt课件

这是一份人教B版 (2019)必修 第二册5.3.4 频率与概率多媒体教学ppt课件，共60页。PPT课件主要包含了概率概念的理解，反思感悟，用频率估计概率，≤PA，随堂演练，课时对点练等内容，欢迎下载使用。

1.了解随机事件发生的不确定性和概率的稳定性.
2.正确理解概率的含义，理解频率与概率的区别与联系．
对于样本点等可能的试验，我们可以用古典概型公式计算有关事件的概率，但在现实中，很多试验的样本点往往不是等可能的或者是否等可能不容易判断．例如，抛掷一枚质地不均匀的骰子，或者抛掷一枚图钉，此时无法通过古典概型公式计算有关事件的概率，我们需要寻找新的求概率的方法．
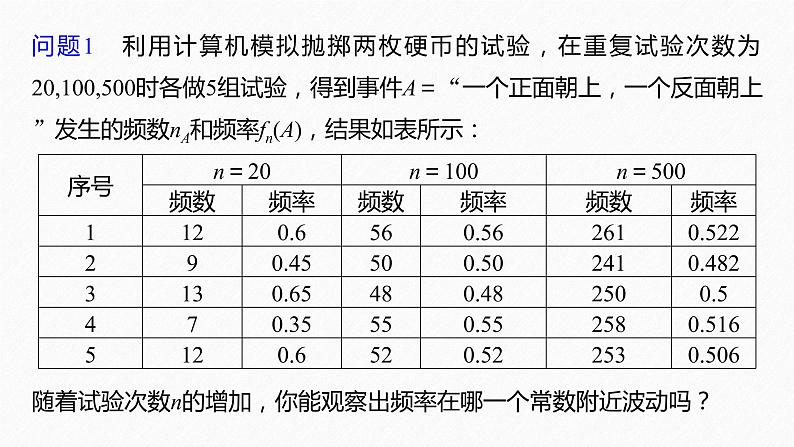
问题1　利用计算机模拟抛掷两枚硬币的试验，在重复试验次数为20,100,500时各做5组试验，得到事件A＝“一个正面朝上，一个反面朝上”发生的频数nA和频率fn(A)，结果如表所示：
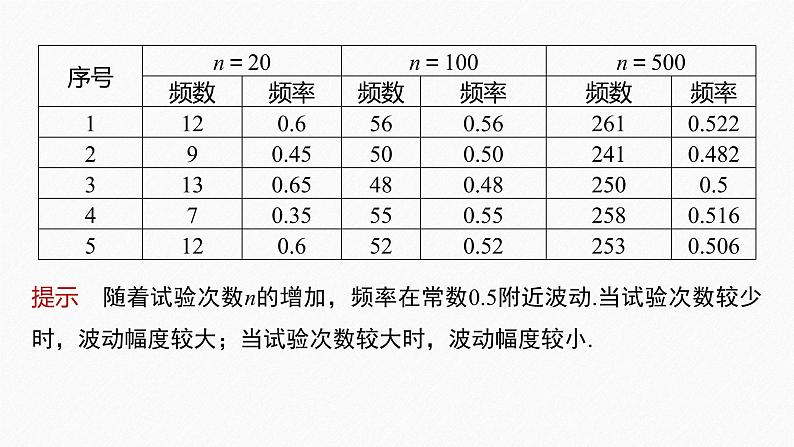
随着试验次数n的增加，你能观察出频率在哪一个常数附近波动吗？
提示　随着试验次数n的增加，频率在常数0.5附近波动.当试验次数较少时，波动幅度较大；当试验次数较大时，波动幅度较小.
1.事实上，大数定律能够保证，在大量重复的试验过程中，一个事件发生的频率会很接近于这个事件发生的概率，而且，试验的次数越多，频率与概率之间差距很小的可能性越大.2.概率是一个确定的数，与每次的试验无关.
　　解释下列概率的含义.(1)某厂生产产品的合格率为0.9；
“某厂生产产品的合格率为0.9”.说明该厂产品合格的可能性为90%，也可以说100件该厂的产品中大约有90件是合格的.
(2)一次抽奖活动中，中奖的概率为0.2.
“中奖的概率为0.2”.说明参加抽奖的人有20%的可能中奖，也可以说，若有100人参加抽奖，约有20人中奖.
概率是事件的本质属性，不随试验次数的变化而变化，概率反映了事件发生的可能性的大小，但概率只提供了一种“可能性”，而不是试验总次数中某一事件一定发生的比例，即使是大概率事件，也不能肯定事件一定发生，只是认为发生的可能性大.
　　　(1)(多选)下列说法正确的是A.由生物学知道生男生女的概率约为0.5，一对夫妇先后生两个小孩，不　一定为一男一女B.一次摸奖活动中，中奖概率为0.2，则摸5张票，一定有一张中奖C.10张票中有1张奖票，10人去摸，谁先摸则谁摸到奖票的可能性大D.10张票中有1张奖票，10人去摸，无论谁先摸，摸到奖票的概率都是0.1
一对夫妇生两个小孩可能是(男，男)，(男，女)，(女，男)，(女，女)，所以A正确；中奖概率为0.2是说中奖的可能性为0.2，当摸5张票时，可能都中奖，也可能中一张、两张、三张、四张或者都不中奖，所以B不正确；10张票中有1张奖票，10人去摸，每人摸到的可能性是相同的，即无论谁先摸，摸到奖票的概率都是0.1，所以C不正确，D正确.
(2)某工厂生产的产品合格率是99.99%，这说明A.该厂生产的10 000件产品中不合格的产品一定有1件B.该厂生产的10 000件产品中合格的产品一定有9 999件C.合格率是99.99%，很高，说明该厂若只生产1件产品一定会合格D.该厂生产的一件产品合格的可能性是99.99%
合格率是99.99%，是指该工厂生产的每件产品合格的可能性大小，即合格的概率.
问题2　在问题1中，频率与概率有什么关系？
提示　(1)试验次数n相同，频率fn(A)可能不同，这说明随机事件发生的频率具有随机性.(2)从整体来看，频率在概率0.5附近波动.当试验次数较少时，波动幅度较大；当试验次数较大时，波动幅度较小，但试验次数多的波动幅度并不全都比次数少的小，只是波动幅度小的可能性更大.
用频率估计概率一般地，如果在n次重复进行的试验中，事件A发生的频率为 ，则当n很大时，可以认为事件A发生的概率P(A)的估计值为 ，此时也有________ .这种确定概率估计值的方法称为用频率估计概率.
　　某商场设立了一个可以自由转动的转盘(如图所示)，并做如下规定：顾客购物80元以上就获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据：
(1)计算并完成表格(精确到0.01)；
落在区域“1”的频率如下表
(2)当n很大时，落在区域“1”的频率将会接近多少？
由(1)中计算的频率，可判断当n很大时，落在区域“1”的频率将会接近0.12.
(3)你获得区域“1”相应奖品的概率大约为多少？
由(1)，(2)及频率与概率的关系可知获得区域“1”相应奖品的概率大约为0.12.
随机事件概率的理解及求法(1)理解：概率可看作频率理论上的期望值，它从数量上反映了随机事件发生的可能性的大小.当试验的次数越来越多时，频率越来越趋近于概率.当次数足够多时，所得频率就近似地看作随机事件的概率.(2)求法：通过公式fn(A)＝　　　计算出频率，再由频率估算概率.
　　　某射击运动员进行双向飞碟射击训练，各次训练的成绩记录如下：
(1)将各次训练记录击中飞碟的频率填入表中(精确到0.01)；
表中由左至右，依次填入的数据是0.81，0.79,0.82,0.82,0.79,0.79,0.81.
(2)这个运动员击中飞碟的概率约为多少(精确到0.01)?
由于频率稳定在常数0.80附近，所以这个运动员击中飞碟的概率约为0.80.
由频率分布直方图估计概率
　　某篮球运动员统计了他最近几次参加比赛投篮的得分情况，得到的数据如下表所示：
注：每次投篮，要么得两分，要么得三分，要么没投中得零分.(1)该篮球运动员有多少次投篮没投中？
该篮球运动员投篮没投中的次数为75－(45＋12)＝18.
(2)记该篮球运动员在一次投篮中，投中两分为事件A，投中三分为事件B，没投中为事件C，试估计P(A)，P(B)，P(C).
所以可以估计P(A)＝0.6，P(B)＝0.16.
(1)频数、频率分布图表中各频数、频率或各小区间内的频数(频率)对应的事件是互斥的.(2)两对立事件的概率和为1以及互斥事件的概率加法公式在频率估计概率时仍成立.
　　　为了了解某次数学考试全校学生的得分情况，数学老师随机选取了若干名学生的成绩，并以[50,60)，[60,70)，…，[90,100]为分组，作出了如图所示的频率分布直方图.从该学校中随机选取一名学生，估计这名学生该次数学考试成绩在[80,100]内的概率.
由频率分布直方图可以看出，所抽取的学生成绩中，在[80,100]内的频率为(0.03＋0.01)×(90－80)＝0.4.因为由样本的分布可以估计总体的
分布，所以全校学生的数学得分在[80,100]内的频率可以估计为0.4.根据用频率估计概率的方法可知，随机选取一名学生，这名学生该次数学考试成绩在[80,100]内的概率可以估计为0.4.
1.知识清单： (1)理解概率的意义. (2)频率与概率的关系. (3)用频率估计概率.2.方法归纳：极限法.3.常见误区：频率与概率的区别与联系.
由概率的意义知，第5个病人的治愈率仍为 ，与前4个病人都没治好没有关系.
2.抛掷一枚质地均匀的硬币，如果连续抛掷1 000次，那么第999次出现正面朝上的概率是
抛掷一枚质地均匀的硬币，只考虑第999次，有两种结果：正面朝上，反面朝上，每种结果等可能出现，故所求概率为 .
3.从存放号码分别为1,2，…，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：
则取到号码为奇数的频率是 B.0.5
4.经过市场抽检，质检部门得知市场上各品牌食用油合格率为80%，经调查，某市市场上的食用油大约有80个品牌，则不合格的食用油品牌大约有A.64个 　　　　　B.6个 　　　　　C.16个 　　　　　D.8个
80×(1－80%)＝16.
5.如果袋中装有数量差别很大而大小相同的白球和黄球(只是颜色不同)若干个，从中任取一球后放回，取了10次有7次是白球，估计袋中数量较多的是____球.
取出白球的频率是0.7，估计其概率是0.7，那么取出黄球的概率约是0.3，取出白球的概率大于取出黄球的概率，所以估计袋中数量较多的是白球.
1.(多选)“今天北京的降雨概率是80%，上海的降雨概率是20%”，下列说法正确的是A.北京今天一定降雨，而上海一定不降雨B.上海今天可能降雨，而北京可能没有降雨C.今天北京和上海都可能没降雨D.北京今天降雨的可能性比上海大
北京的降雨概率80%大于上海的降雨概率20%，说明北京降雨的可能性比上海大，也可能都降雨，也可能都没有降雨，但是不能确定北京今天一定降雨，上海一定不降雨，所以B，C，D正确，A错误.
2.(多选)以下说法错误的是A.昨天没有下雨，则说明“昨天气象局的天气预报降水的概率为99%” 是错误的B.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖C.做10次抛掷硬币的试验，结果3次正面朝上，因此正面朝上的概率为D.某厂产品的次品率为2%，但该厂的50件产品中可能有2件次品
A中，降水概率为99%，仍有不降水的可能，故错误；B中，“彩票中奖的概率是1%”表示在设计彩票时，有1%的机会中奖，但不一定买100张彩票一定有1张会中奖，故错误；
D中，次品率为2%，但50件产品中可能没有次品，也可能有1件或2件或3件或更多次品，故正确.
3.我国古代数学名著《数学九章》有“米谷粒分”题：粮仓开仓收粮，有人送来米1 534石，验得米夹谷，抽样取米一把，数得254粒夹谷28粒.这批米夹的谷约为A.134石 　　　B.169石 　　　C.338石 　　　D.454石
4.先后抛掷两枚均匀的五角、一元的硬币，观察落地后硬币的正反面情况，则下列哪个事件的概率最大A.至少一枚硬币正面向上B.只有一枚硬币正面向上C.两枚硬币都是正面向上D.两枚硬币都是反面向上
抛掷两枚硬币，其结果有“正、正”“正、反”“反、正”“反、反”四种情况，至少一枚硬币正面向上包括三种情况，其概率最大.
5.某市交警部门在调查一起车祸过程中，所有的目击证人都指证肇事车是一辆普通桑塔纳出租车，但由于天黑，均未看清该车的车牌号码及颜色，而该市有两家出租车公司，其中甲公司有100辆桑塔纳出租车，3 000辆帕萨特出租车，乙公司有3 000辆桑塔纳出租车，100辆帕萨特出租车.交警部门应先调查哪家公司的车辆较合理？A.甲公司　　　B.乙公司　　　C.甲与乙公司　　　D.以上都对
6.空气质量指数(AQI)是定量描述空气质量状况的无量纲指数，AQI的数值越大、级别和类别越高，说明空气污染状况越严重.当空气质量指数在0～50时，空气质量指数级别为一级(优)；当空气质量指数在51～100时，空气质量指数级别为二级(良)……为了加强环境保护，治理空气污染，环境监测部门对某市2021年的空气质量进行调研，随机抽取了100天的空气质量指数(AQI)，得下表：
依据上表，估计该市某一天的空气质量指数级别为一级(优)的概率是________.
当空气质量指数级别为一级(优)时，空气质量指数在0～50, 共有8＋21＋22＝51(天)，则样本中空气质量指数级别为一级(优)的频率为 ＝0.51，
故估计该市某一天的空气质量指数级别为一级(优)的概率是 ＝0.51.
7.投掷硬币的结果如下表：
据此可估计若掷硬币一次，正面向上的概率为________.
易知正面向上的频率在0.5附近，所以若掷硬币一次，正面向上的概率应为0.5.
8.对某厂生产的某种产品进行抽样检查，数据如下表所示：
根据表中所提供的数据，若要从该厂生产的此种产品中抽950件合格品，大约需抽查________件产品.
由表中数据知，抽查5次，产品合格的频率依次为0.94,0.92,0.96,0.95,0.956，可见频率在0.95附近摆动，故可估计该厂生产的此种产品合格的概率约为0.95.
设大约需抽查n件产品，则 ＝0.95，所以n＝1 000.
9.某中学从参加高一年级上学期期末考试的学生中抽出60名学生，将其成绩(均为整数)分成[40,50)，[50,60)，…，[90,100]六段后画出如图所示的频率分布直方图.观察图形的信息，
回答下列问题：(1)估计这次考试的及格率(60分及以上为及格)；
依题意，60分及以上的分数所在的第三、四、五、六组的频率和为(0.015＋0.03＋0.025＋0.005)×10＝0.75，所以估计这次考试的及格率约为75%.
(2)从成绩在70分以上(包括70分)的学生中任选一人，求选到第一名学生的概率(第一名学生只一人).
因为成绩在[70,100]的人数是60×(0.03＋0.025＋0.005)×10＝36，所以从成绩在70分以上(包括70分)的学生中任选一人，
10.有三张除字母外完全相同的纸牌，字母分别是K，K，Q.进行有放回的抽样，每次试验抽出一张纸牌，经过多次试验后结果汇总如下表：
(1)将上述表格补充完整；
完善后表格如下表所示：
(2)观察表格，计算摸到K的频率为多少；
由(1)可得摸到K的频率约为66%.
(3)估计摸到K的概率.
由频率与概率的关系可得，摸到K的概率约为66%，事实上摸到K的概率为 .
11.随着互联网的普及，网上购物已逐渐成为消费时尚，为了解消费者对网上购物的满意情况，某公司随机对4 500名网上购物消费者进行了调查(每名消费者限选一种情况回答)，统计结果如下表：
根据表中数据，估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率是
由题意得，n＝4 500－200－2 100－1 000＝1 200，所以随机调查的消费者中对网上购物“比较满意”或“满意”的总人数为1 200＋2 100＝3 300，所以随机调查的消费者中对网上购物“比较满意”或“满意”的频率为 .
由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为 .
12.已知某射击运动员，每次击中目标的概率都是0.8.现采用随机模拟的方法估计该运动员射击4次至少击中3次的概率：用计算机随机模拟产生0到9之间取整数值的随机数，指定0,1表示没有击中目标，2,3,4,5,6,7,8,9表示击中目标；因为射击4次，故以每4个随机数为一组，代表射击4次的结果.经随机模拟产生了如下20组随机数：5727　0293　7140　9857　0347　4373　86369647　1417　4698　0371　6233　2616　80456011　3661　9597　7424　6710　4281据此估计，该射击运动员射击4次至少击中3次的概率为A.0.7 　　　　 　　　　C.0.8 　　　　
在20组随机数中表示射击4次至少击中3次的有5727,0293,9857,0347,4373,8636,9647,4698,6233,2616,8045,3661,9597,7424,4281，共15组随机数，
13.一个容量为20的样本，数据的分组及各组的频数如下：[10,20)，2个；[20,30)，3个；[30,40)，x个；[40,50)，5个；[50,60)，4个；[60,70]，2个.则x＝___；根据样本的频率估计概率，数据落在[10,50)的概率约为____.
样本中数据总个数为20，∴x＝20－(2＋3＋5＋4＋2)＝4；在[10,50)中的数据有14个，
14.若某地8月15日无雨记为0，有雨记为1，统计从1995年至2019年的气象资料得：11000　10011　00001　01011　10100，则该地出现8月15日下雨的概率约为________.
根据所统计的25年的资料，共有11次有雨，因此该地8月15日下雨的概率约为　＝0.44.
15.某公司有5万元资金用于投资开发项目，如果成功，一年后可获收益12%；一旦失败，一年后将丧失全部资金的50%.下表是去年200例类似项目开发的实施结果.
则估计该公司一年后可获收益的平均数是_____万元.
应先求出投资成功与失败的概率，再计算收益的平均数.
设可获收益为x万元，如果成功，x的取值为5×12%，如果失败，x的取值为－5×50%.
16.某高中启动了“全民阅读，书香校园”活动，在活动期间用简单随机抽样方法，抽取了30名同学，对其每月平均课外阅读时间(单位：小时)进行调查，所得数据的茎叶图如图所示.将月均课外阅读时间不低于30小时的学生称为“读书迷”.
(1)将频率视为概率，试估计该校900名学生中“读书迷”有多少人；
设该校900名学生中“读书迷”有x人，由茎叶图得30名学生中有7名学生月均课外阅读时间不低于30小时，
故估计该校900名学生中“读书迷”有210人.
(2)从已抽取的7名“读书迷”中随机抽取男、女“读书迷”各1人，参加读书日宣传活动.①共有多少种不同的抽取方法？
由茎叶图得7名“读书迷”中男生有3人，设为a35，a38，a41，女生有4人，设为b34，b36，b38，b40(其中符号下标表示该学生月均课外阅读时间)，
则从7名“读书迷”中随机抽取男、女“读书迷”各1人的样本空间Ω＝{(a35，b34)，(a35，b36)，(a35，b38)，(a35，b40)，(a38，b34)，(a38，b36)，(a38，b38)，(a38，b40)，(a41，b34)，(a41，b36)，(a41，b38)，(a41，b40)}，共包含12个样本点，所以共有12种不同的抽取方法.
②求抽取的男、女两位‘读书迷’月均课外阅读时间相差不超过2小时的概率.
设A表示事件“抽取的男、女两位‘读书迷’月均课外阅读时间相差不超过2小时”.
由①得事件A包含(a35，b34)，(a35，b36)，(a38，b36)，(a38，b38)，(a38，b40)，(a41，b40)，共6个样本点，
所以抽取的男、女两位“读书迷”月均课外阅读时间相差不超过2小时的概率为 .