北师大版 (2019)必修 第一册2.1 古典概型评课课件ppt

这是一份北师大版 (2019)必修 第一册2.1 古典概型评课课件ppt，文件包含培优课与古典概型相关的问题pptx、培优课与古典概型相关的问题doc等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

概率不仅是高中的重要内容，也是高考的主要考点之一.古典概型主要考查学生的列举归纳和逻辑推理素养，常与互斥事件、对立事件、相互独立事件以及抽样方法等知识相联系，对于古典概型的常考问题归纳如下.
类型一　“放回”、“不放回”问题与古典概型
“放回”与“不放回”的主要区别是放回抽样时总体个数不发生变化，样本点的总数不变；而不放回抽样时，总体个数减少，样本点的总数减少.
例1　一个不透明的袋子中装有5个小球，其中有3个红球，2个白球，这些球除颜色外完全相同.(1)记事件A为“一次摸出2个球，摸出的球为一个红球，一个白球”.求P(A)；
类型二　抽样方法与古典概型
古典概型常与抽样中的分层抽样相结合，首先利用抽样方法得到适合条件的事件的个数，然后利用古典概型概率公式求概率，在求概率时找准样本点个数是解题的关键.样本点的探求方法有 (1)枚举法：适合给定的样本点个数较少且易一一列举出的；(2)树状图法：适合于较为复杂的问题中的样本点的探求.在找样本点个数时，一定要按顺序逐个写出：先(A1，B1)，(A1，B2)，…，(A1，Bn)，再(A2，B1)，(A2，B2)，…，(A2，Bn)，依次(A3，B1)，(A3，B2)，…，(A3，Bn)，… ，这样写可有效避免重写、漏写.
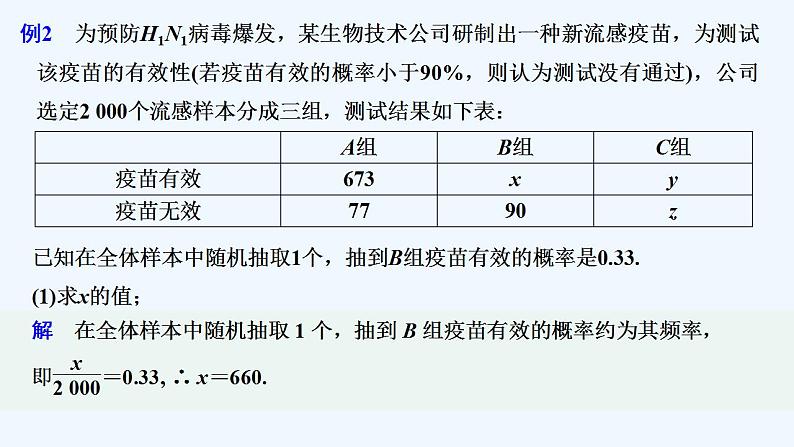
例2　为预防H1N1病毒爆发，某生物技术公司研制出一种新流感疫苗，为测试该疫苗的有效性(若疫苗有效的概率小于90%，则认为测试没有通过)，公司选定2 000个流感样本分成三组，测试结果如下表：
已知在全体样本中随机抽取1个，抽到B组疫苗有效的概率是0.33.(1)求x的值；
(2)现用分层随机抽样的方法在全体样本中抽取360个测试结果，问应在C组抽取多少个？
解　C组样本个数为y＋z＝2 000－(673＋77＋660＋90)＝500，
(3)已知y≥465，z≥30，求不能通过测试的概率.解　设测试不能通过事件为A，C组疫苗有效与无效的可能的情况记为(y，z)，由(2)知y＋z＝500，且y，z∈N，样本空间包含的样本点有：(465，35)，(466，34)，(467，33)，…，(470，30)共6个.若测试不能通过，则77＋90＋z>200，即z>33，事件A包含的样本点有：(465，35)，(466，34)共2个.
类型三　互斥事件、对立事件与古典概型
此类问题要首先判断事件间的关系是否为互斥或对立，对互斥事件每种情况下的概率利用古典概型计算，然后利用互斥事件的求和公式得到所求事件的概率；若为对立事件，则可用两种方法解决，一是直接法：分类考虑，分别求事件的概率，然后求和；二是间接法：利用两对立事件之间的关系，概率之和为1求概率，但每种情况都需要利用古典概型的概率公式计算出概率.
例3　某商场举行购物抽奖促销活动，规定每位顾客从装有编号为0，1，2，3四个相同小球的抽奖箱中，每次取出一球，记下编号后放回，连续取两次，若取出的两个小球号码之和等于6，则中一等奖，等于5中二等奖，等于4或3中三等奖，其他情况不中奖.(1)求中三等奖的概率；
(3)求未中奖的概率.
类型四　方案选取与古典概型
所谓方案的选取主要是利用概率的大小得到方案的合理性或公平性，其关键是利用古典概型计算每种方案的概率，然后再比较方案的合理性.
(2)试比较每对亲子获得汽车玩具与获得饮料的概率，哪个更大？请说明理由.解　记“获得汽车玩具”为事件B，“获得饮料”为事件C，
所以每对亲子获得汽车玩具的概率小于获得饮料的概率.
类型五　统计图表与古典概型
统计图表与古典概型的问题，主要是以统计图表为载体，需要从统计图表中提取相关信息，然后利用古典概型计算概率.
例5　已知国家某大型5A级景区对拥挤等级与每日游客数量n(单位：百人)的关系有如下规定：当n∈[0，100)时，拥挤等级为“优”；当n∈[100，200)时，拥挤等级为“良”；当n∈[200，300)时，拥挤等级为“拥挤”；当n≥300时，拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据：
(1)下面是根据统计数据得到的频率分布表，求出a，b的值，并估计该景区6月份游客人数的平均值.(同一组中的数据用该组区间的中点值作代表)
(2)某人选择在6月1日至6月5日这5天中任选2天到该景区游玩，求他这2天遇到的游客拥挤等级均为“优”的概率.解　从5天中任选2天，试验的样本空间Ω＝{(1，2)，(1，3)，(1，4)，(1，5)，(2，3)，(2，4)，(2，5)，(3，4)，(3，5)，(4，5)}，共10个样本点，其中游客拥挤等级均为“优”的有(1，4)，(1，5)，(4，5)，共3个，