人教A版 (2019)必修 第一册3.2 函数的基本性质教课内容ppt课件

这是一份人教A版 (2019)必修 第一册3.2 函数的基本性质教课内容ppt课件，共30页。PPT课件主要包含了fx≤M，fx≥M，迁移探究等内容，欢迎下载使用。
[课程目标] 1.理解函数的最大(小)值的概念及其几何意义； 2.理解函数的最大(小)值是在整个定义域上研究函 数，体会求函数最值是函数单调性的应用之一； 3.会求一些简单函数的最值．
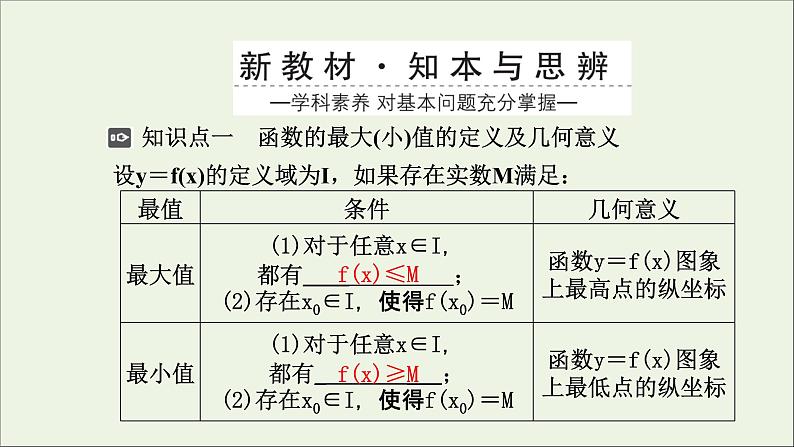
知识点一　函数的最大(小)值的定义及几何意义设y＝f(x)的定义域为I，如果存在实数M满足：
【思辨】 判断正误(请在括号中打“√”或“×”).(1)函数f(x)＝－x2＋1≤2总成立，则f(x)的最大值是2.(　　)(2)函数的最大值或最小值一定是函数值域中的元素.(　　)(3)函数f(x)的值域是(0，＋∞)，则函数f(x)的最小值为0.(　　)(4)若函数f(x)在区间[a，b]上具有单调性，则f(a)或f(b)是函 数f(x)的最大值或最小值．(　　)
【解析】 (1)函数f(x)的定义域中不存在x0，使f(x0)＝2，所以2不是f(x)的最大值．(2)函数的最大值和最小值也是函数值，所以函数的最大值或最小值一定是函数值域中的元素．(3)函数的值域中不包含0，所以0不是函数的最小值．(4)根据函数最大(小)值的定义知说法正确．
知识点二　求函数的最值的常用方法1．图象法：作出y＝f(x)的图象，观察最高点与最低点，最高 (低)点的纵坐标即为函数的最大(小)值．2．运用已学函数的值域．3．运用函数的单调性 (1)若判断y＝f(x)在区间[a，b]上单调递增， 则ymax＝__________，ymin＝_______． (2)若判断y＝f(x)在区间[a，b]上单调递减， 则ymax＝________，ymin＝__________．
(3)若y＝f(x)是定义在区间(a，b)或R上的连续函数，则函 数y＝f(x)的最大(小)值要根据具体函数而定．4．分段函数的最大(小)值是指各段上的最大(小)值中的最大 (小)的那个．
【思辨】 判断正误(请在括号中打“√”或“×”).(1)函数y＝－2x＋3在(2，5]上有最小值－7，没有最大值．( 　)(2)函数y＝在[1，2]上有最大值1，最小值.(　　)(3)函数y＝x2＋2x＋3的最小值为2.(　　)(4)函数y＝x2＋2x＋4(x∈[－3，－2])的最小值为2.(　　)
例1 已知函数f(x)＝x2－2ax＋3，求f(x)在区间[0，2]上的最小值g(a)和最大值h(a).
1．求函数f(x)＝x2－2ax＋2在[－1，1]上的最小值． 解：函数f(x)图象的对称轴为直线x＝a，且函数图象开口 向上，
2．已知函数f(x)＝x2＋4x＋3，求f(x)在区间[t，t＋1]上的最小 值g(t)和最大值h(t).
例2 某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t，P)，点(t，P)落在如图所示中的两条线段上．该股票在30天内的日交易量Q(万股)与时间t(天)的部分数据如下表所示：(1)根据提供的图象，写出该股票每股交易价格P(元)与时间t(天)所满足的函数关系式；
(2)根据表中数据，确定该股票日交易量Q(万股)与时间t(天)的函数关系式；(3)用y表示该股票日交易额(万元)，写出y关于t的函数关系式，并求出在这30天中第几天日交易额最大，最大是多少．
[规律方法]1．分段函数的最大值为各段上最大值的最大者，最小值为各 段上最小值的最小者，故求分段函数的最大或最小值，应 先求各段上的最值，再比较即可得函数的最大、最小值．2．如果函数的图象容易作出，画出分段函数的图象，观察图 象的最高点与最低点，并求其纵坐标即可得函数的最大 值、最小值．
设函数f(x)＝x|x－1|＋m，当m>1时，求f(x)在[0，m]上的最大值．
例3 已知函数f(x)＝ ，x∈[2，＋∞).(1)求f(x)的最小值；(2)若f(x)>a恒成立，求a的取值范围．
求函数f(x)＝在区间[1，2]上的最大值和最小值．
[规律方法]1．函数的最值与单调性的关系． (1)若f(x)在[a，b]上单调递减，则f(x)在[a，b]上的最大值为 f(a)，最小值为f(b)； (2)若f(x)在[a，b]上单调递增，则f(x)在[a，b]上的最大值为 f(b)，最小值为f(a).2．利用函数的单调性求最值，要熟练掌握一些常见函数的基 本性质．
1．函数f(x)的部分图象如图所示，则该函数在[－2，2]上的最 小值、最大值分别是(　　)A．f(－2)，f(3)B．0，2C．f(－2)，2D．f(2)，2【解析】 由图象可知，x＝－2时，f(x)取得最小值f(－2)；x＝1时，f(x)取得最大值f(1)＝2.故选C.
2．函数y＝2x2＋1，x∈N*的最值情况是(　　)A．无最大值，最小值是1B．无最大值，最小值是3C．无最大值，也无最小值D．不能确定最大、最小值【解析】 因为x∈N*，且函数在(0，＋∞)上单调递增，故函数在x＝1时取得最小值，最小值为3，无最大值．故选B.
3．函数 在区间上的最大值是(　　)