2020-2021学年8.5 空间直线、平面的平行同步达标检测题

这是一份2020-2021学年8.5 空间直线、平面的平行同步达标检测题，文件包含852直线与平面平行提升练-2020-2021学年下学期高一数学同步课堂人教A版2019必修第二册解析版doc、852直线与平面平行提升练-2020-2021学年下学期高一数学同步课堂人教A版2019必修第二册原卷版doc等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
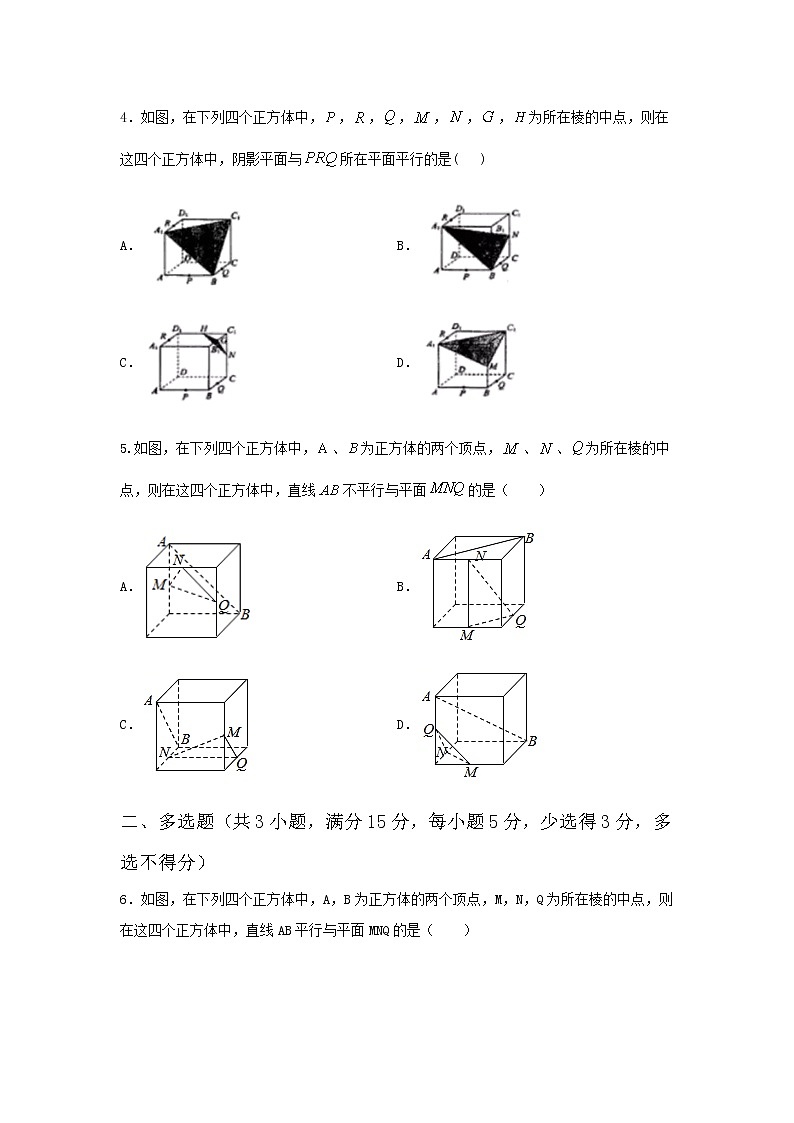
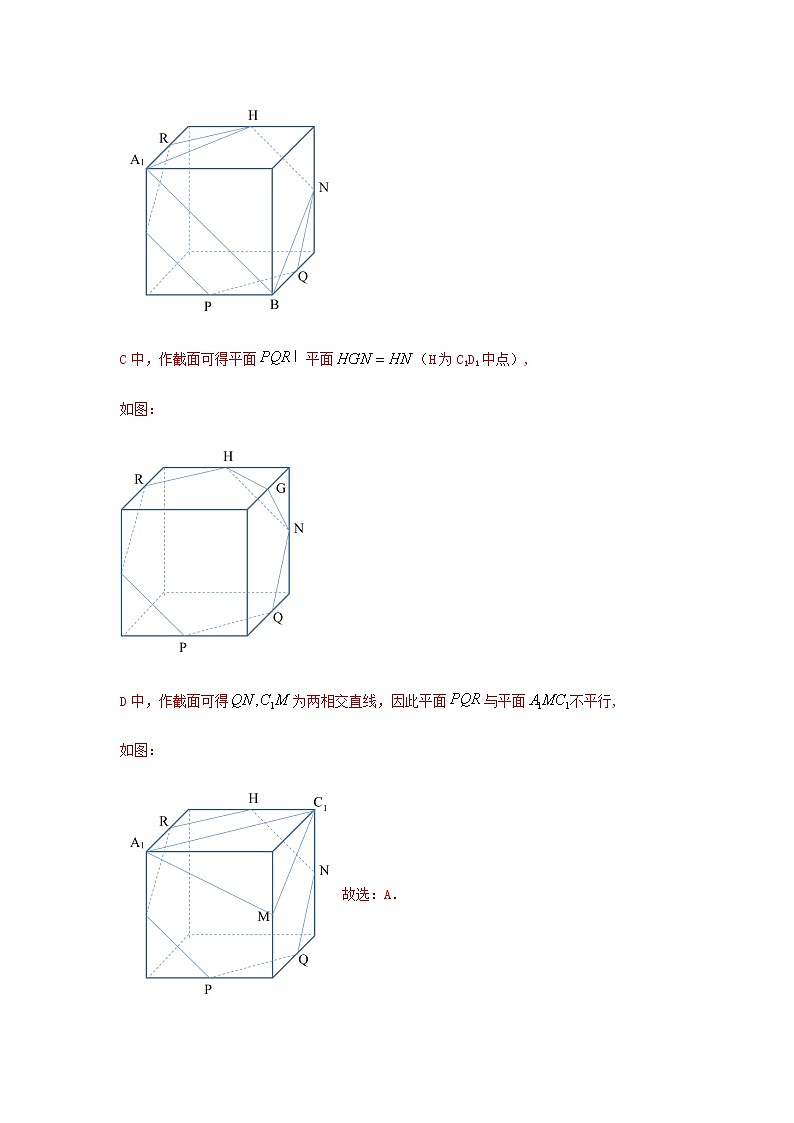
第八章 立体几何初步8.5.2直线与平面平行(提升练）一、单选题（共5小题，满分25分，每小题5分）1.已知直线l和平面α，若，，则过点P且平行于l的直线（    ）A．只有一条，不在平面α内                     B．只有一条，且在平面α内C．有无数条，一定在平面α内                   D．有无数条，一定不在平面α内【答案】B【解析】假设过点P且平行于的直线有两条与，∴且，由平行公理得，这与两条直线与相交与点相矛盾,   故选:B2．如图，四棱锥中，，分别为，上的点，且平面，则　　A． B． C． D．以上均有可能【答案】B【解析】四棱锥中，，分别为，上的点，且平面，平面，平面平面，由直线与平面平行的性质定理可得：．故选：B．3．下列结论：①如果一条直线不在平面内，则这条直线就与这个平面平行；②过直线外一点，可以作无数个平面与这条直线平行；③如果一条直线与平面平行，则它与平面内的任何直线平行.其中正确结论的个数为(　 　)A．0个　　　　　　 B．1个　　　　　　C．2个　　　　　　 D．3个【解析】①中，直线可能与平面相交，故①错；②是正确的；③中，一条直线与平面平行，则它与平面内的直线平行或异面，故③错.故选：B．4．如图，在下列四个正方体中，，，，，，，为所在棱的中点，则在这四个正方体中，阴影平面与所在平面平行的是(   )A． B．C． D．【答案】A【解析】A中，因为,所以可得平面,又，可得平面，从而平面平面B中，作截面可得平面平面（H为C1D1中点）,如图：C中，作截面可得平面平面（H为C1D1中点）,如图：D中，作截面可得为两相交直线，因此平面与平面不平行,如图：故选：A．5.如图，在下列四个正方体中，、为正方体的两个顶点，、、为所在棱的中点，则在这四个正方体中，直线不平行与平面的是（　　）A． B．C． D．【答案】D【解析】对于选项A，如下图所示，连接，  在正方体中，且，所以，四边形为平行四边形，则，、分别为、的中点，则，，平面，平面，平面；对于选项B，连接，如下图所示：在正方体中，且，所以，四边形为平行四边形，则，、分别为、的中点，则，，平面，平面，平面；对于选项C，连接，如下图所示：在正方体中，且，所以，四边形为平行四边形，则，、分别为、的中点，则，，平面，平面，平面；对于选项D，如下图所示，连接交于点，连接，连接交于点，若平面，平面，平面平面，则，则，由于四边形为正方形，对角线交于点，则为的中点，、分别为、的中点，则，且，则，，则，又，则，所以，与平面不平行；故选：D.二、多选题（共3小题，满分15分，每小题5分，少选得3分，多选不得分）6．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB平行与平面MNQ的是（　　）A. B.C. D.【答案】ABC【解析】对于选项A，由于AB∥NQ，结合线面平行判定定理可知A满足题意；对于选项B，由于AB∥MQ，结合线面平行判定定理可知B满足题意；对于选项C，由于AB∥MQ，结合线面平行判定定理可知C满足题意；对于选项D，由于直线AB不平行与平面MNQ，不满足题意.故选：ABC7．如图所示,P为矩形所在平面外一点,矩形对角线的交点为为的中点,给出以下结论,其中正确的是(    )A． B．平面C．平面 D．平面【答案】ABC【解析】由题意知,是的中位线,,故正确;平面,平面,平面,故正确;同理,可得平面,故正确;与平面和平面都相交,故不正确.  故选：ABC．8．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ平行的是(　 　)【解析】选项B中，AB∥MQ，且AB⊄平面MNQ，MQ⊂平面MNQ，则AB∥平面MNQ；选项C中，AB∥MQ，且AB⊄平面MNQ，MQ⊂平面MNQ，则AB∥平面MNQ；选项D中，AB∥NQ，且AB⊄平面MNQ，NQ⊂平面MNQ，则AB∥平面MNQ.   故选:BCD．三、填空题（共3小题，满分15分，每小题5分，一题两空，第一空2分）9．下列三个命题在“_______”处都缺少同一个条件，补上这个条件使其构成真命题（其中为直线，为平面），则此条件是__________.①；②；③【答案】【解析】①，或，由；②，，；③，或，由．故答案为：．10．如图，四棱锥S-ABCD的所有棱长都等于2，E是SA的中点，过C，D，E三点的平面与SB交于点F，则四边形DEFC为___________形，其周长为___________．【答案】梯形    【解析】因为AB=BC=CD=DA=2，所以四边形ABCD是菱形，所以CD∥AB，又CD⊄平面SAB，AB⊂平面SAB，所以CD∥平面SAB.又CD⊂平面CDEF，平面CDEF∩平面SAB=EF，所以CD∥EF，则四边形DEFC为梯形，又EF∥AB.又因为E为SA中点，所以EF=AB=1.因为△SAD和△SBC都是等边三角形，所以DE=CF=2×sin60°=，所以梯形DEFC的周长为：CD+DE+EF+FC=.故答案为：梯形   11．如图，已知四棱锥的底面是平行四边形，交于点，为中点，在上，，平面，则的值为________【答案】3【解析】如下图所示，设交于点，连接，为的中点，则.由于四边形是平行四边形，，，，，因为平面，平面，平面平面，所以，.故答案为:3四、解答题：（本题共3小题，共45分。解答应写出文字说明、证明过程或演算步骤。）12．已知有公共边AB的两个全等的矩形ABCD和ABEF不同在一个平面内，P，Q分别是对角线AE，BD上的点，且AP＝DQ.求证：PQ∥平面CBE.【答案】证明见解析【解析】　如图，作PM∥AB交BE于点M，作QN∥AB交BC于点N，连接MN，则PM∥QN，＝，＝.∵EA＝BD，AP＝DQ，∴EP＝BQ.又∵AB＝CD，∴PMQN，∴四边形PMNQ是平行四边形，∴PQ∥MN.又∵PQ⊄平面CBE，MN⊂平面CBE，∴PQ∥平面CBE.13．如图所示，在三棱柱ABC－A1B1C1中，AC＝BC，点D是AB的中点，求证：BC1∥平面CA1D.【解析】连接AC1，设AC1∩A1C＝E，则E为AC1的中点，又D为AB的中点，∴DE∥BC1．∵DE⊂平面A1DC，BC1⊄平面A1DC，∴BC1∥平面A1DC.14．如图，在三棱柱中，点分别是棱上的点，点是线段上的动点，.若平面，试判断点的位置.【答案】证明见解析【解析】由题意知平面，过作平面交于，连接.因为平面平面，平面平面，所以.因为平面平面，平面平面，所以，所以四边形是平行四边形，所以.而，所以，故是的中位线.所以是的中点时，平面.