初中数学6 斜边直角边图文ppt课件

这是一份初中数学6 斜边直角边图文ppt课件，共23页。PPT课件主要包含了复习提问，SAS边角边，ASA角边角，AAS角角边，SSS边边边，不一定全等，几何语言，小试牛刀，能力提升，探究应用等内容，欢迎下载使用。

如图，舞台背景的形状是两个直角三角形，每个三角形都有一条直角边被花盆遮住无法测量,工作人员想知道这两个直角三角形是否全等.
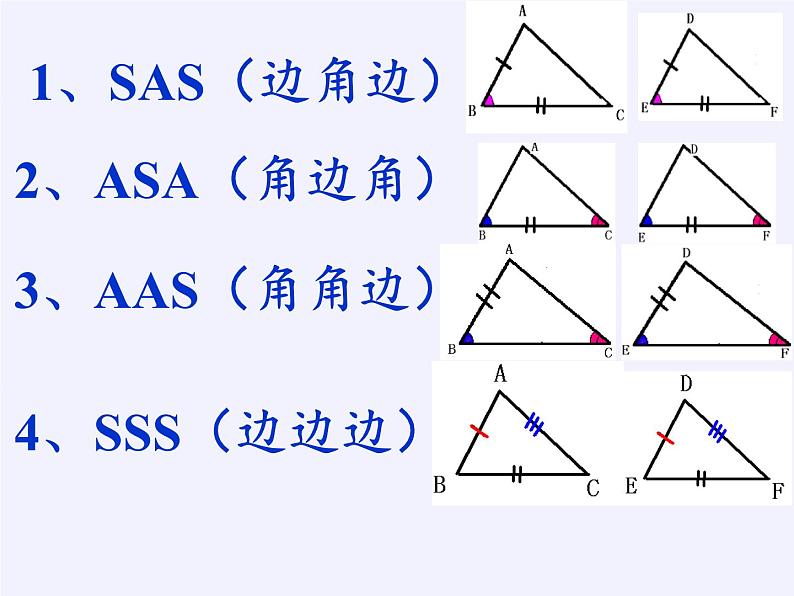
证明两个三角形全等有哪些方法?
两边及其中一边的对角对应相等的两个三角形全等吗?
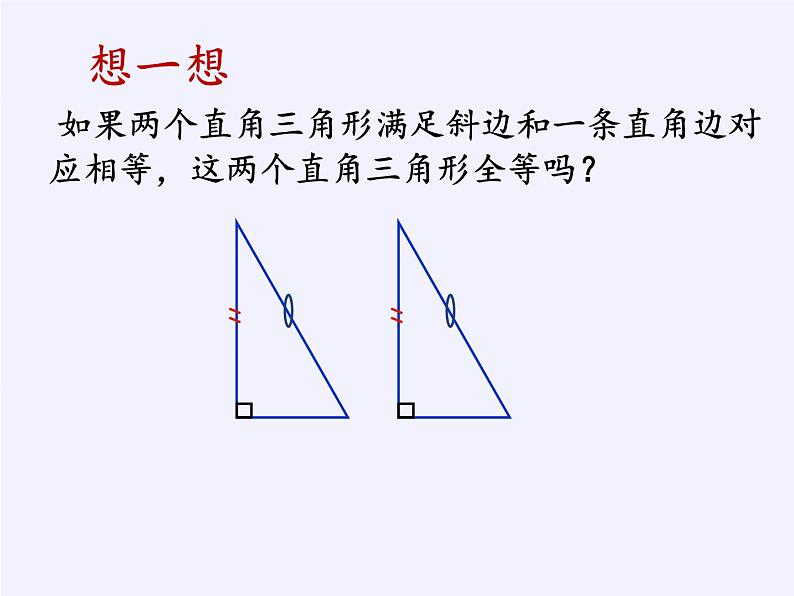
想一想
如果两个直角三角形满足斜边和一条直角边对应相等，这两个直角三角形全等吗？
做一做，说一说 请同学们拿出自己所做的卡片，并与同伴交流。
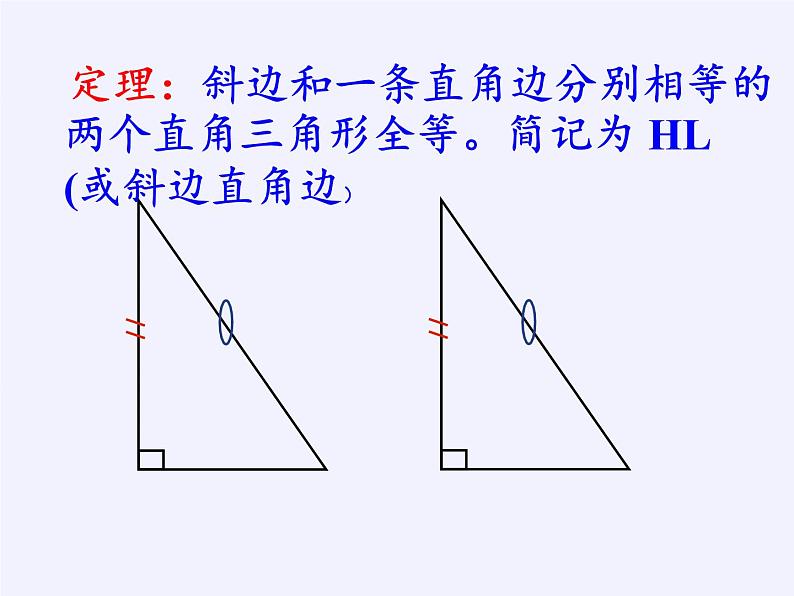
定理：斜边和一条直角边分别相等的两个直角三角形全等。简记为 HL (或斜边直角边）
在Rt△ABC和Rt△AˊBˊCˊ中
∵AB=AˊBˊ AC=AˊCˊ
∴Rt△ABC≌Rt△AˊBˊCˊ（HL）
例1、如图，AC=BD，∠C ﹦∠ D ﹦90°. 求证：BC=AD
证明：∵∠C ﹦∠ D ﹦90°（已知）
∴ 与 都是直角三角形（直角三角形的定义）
在Rt△ABC和Rt△BAD中
∵AB=BA（公共边） AC=BD（已知）
∴Rt△ABC≌Rt△BAD（HL）
∴BC=AD（全等三角形的对应边相等）
1.已知:如图,在△ABC中, D为BC的中点.DE⊥AB,DF⊥AC,点E、F为垂足,DE=DF
求证：△BED≌ △CFD
2.如图，AC=AD，∠C﹦∠D﹦90°， 求证：BC=BD.
若把划线处条件替换为∠ABC=∠ABD 如何证明呢？
已知：如图，AD为△ABC的高，E为 AC上一点，BE交AD于点F，且有
若把划线处条件替换为BD=AD, FD=CD 如何证明呢？
BF=AC,FD=CD
如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系？
∠ABC+∠DFE=90°.
解:在Rt△ABC和Rt△DEF中
∵ BC=EF, AC=DF .
∴ Rt△ABC≌Rt△DEF (H.L.)
∴∠ABC=∠DEF(全等三角形对 应角相等).
∵ ∠DEF+∠DFE=90°(直角三角形两个锐 角互余)
∴∠ABC+∠DFE=90°（等量代换）
灵活运用各种方法证明直角三角形全等
请你谈谈这节课的收获。
作业： 1.课本76页第6题 2.导练101页基础反思
1、如图，AC⊥BC,AC⊥AD,垂足分别是C,A,AB=DC,由此可判定两个全等的三角形是 和
2、如图，在 中，∠C=90 ̊,AC=AE,DE⊥AB,且∠CDA=55̊ ，则∠BDE=
如图，在△ABC中，∠C ﹦90°，AC=10,BC=5.线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AX上运动，当AP= 时，才能使△ABC与△QPA全等。