16.高一数学（人教B版）-已知三角函数值求角-1教案

教学基本信息

课题

已知三角函数值求角

学科

数学

学段： 第二学期

年级

高一

教材

书名：数学必修第三册 出版社：人教B版  出版日期：2019年9月

教学目标及教学重点、难点

本节课的重点是，依据三角函数定义和三角函数的性质与图像，解决已知三角函数值求角的问题.

难点是通过三角函数值（或值的范围），求角的值（或角的范围）的解（解区间）的个数理解三角函数多个自变量对应一个函数值的特点.

教学过程(表格描述)

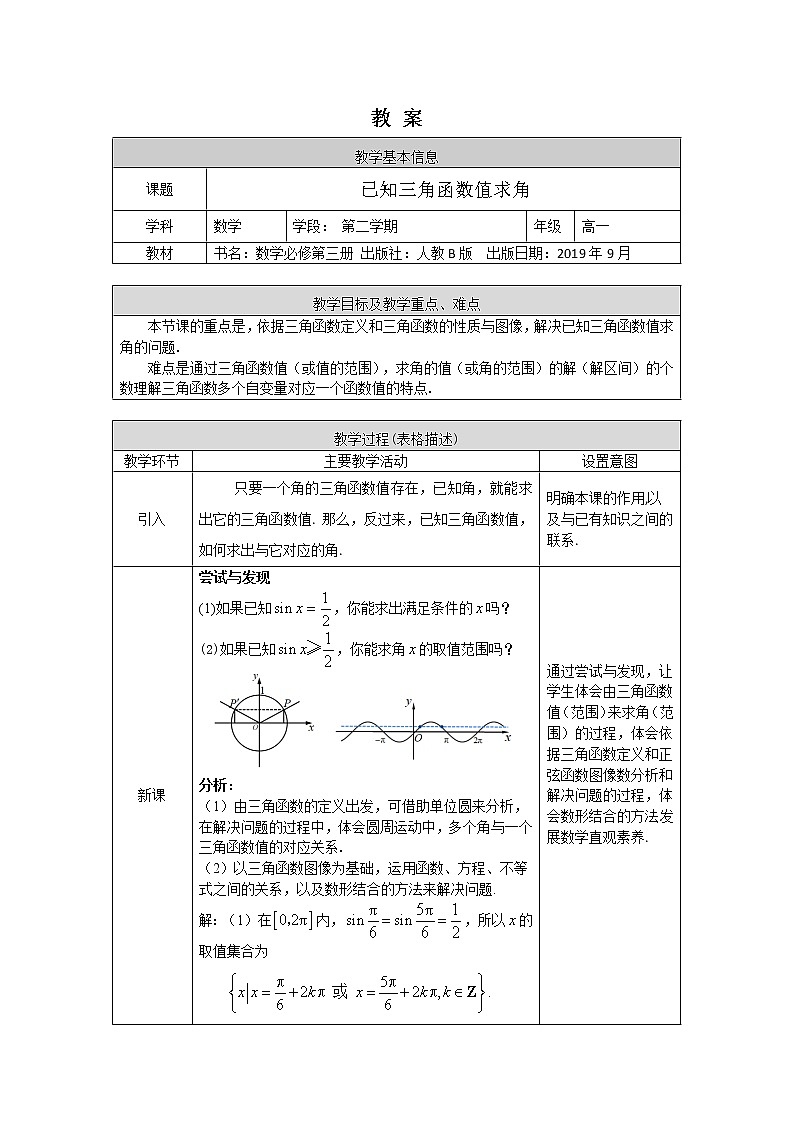
教学环节

主要教学活动

设置意图

引入

 只要一个角的三角函数值存在，已知角，就能求出它的三角函数值. 那么，反过来，已知三角函数值，如何求出与它对应的角.

明确本课的作用,以及与已有知识之间的联系.

新课

尝试与发现

(1)如果已知，你能求出满足条件的吗？

(2)如果已知，你能求角的取值范围吗？

分析：

（1）由三角函数的定义出发，可借助单位圆来分析，在解决问题的过程中，体会圆周运动中，多个角与一个三角函数值的对应关系.

（2）以三角函数图像为基础，运用函数、方程、不等式之间的关系，以及数形结合的方法来解决问题.

解：（1）在内，，所以的取值集合为

.

（2）因为在内，时，所以在上的解集为

通过尝试与发现，让学生体会由三角函数值（范围）来求角（范围）的过程，体会依据三角函数定义和正弦函数图像数分析和解决问题的过程，体会数形结合的方法.发展数学直观素养.

例题

例1已知，求角.

分析：将看成一个整体，由它的三角函数值或值的范围，求得的值或值的范围，再由所得的值或值的范围，求出的值或值的范围.

解：由，求得或，解得x=或.

所以角取值集合为

已知，求角的取值范围.

解：因为，

解得角的取值集合为

已知，且，求角.

解：因为

或

，或

由，可知，或，或或或，

所以，角的取值集合是.

例2 已知，，求.

分析：分别依据正切定义和正切函数图像进行分析，，即点P纵坐标与横坐标之比为，先求得所有满足的角，再在指定范围内确定角.

解：因为，

所以

又因为

所以，,

得到，，得到，或.

的解集:

通过求解关于余弦型函数，已知函数值求角的问题，运用整体求解的方法解决问题，体验解决多重对应关系问题的解决方法.

通过解决在指定范围内，已知三角函数值求角的问题，感受解题程序背后的思维过程.

通过解决在指定范围内，已知正切值（值的范围），求角（角的范围）的问题，体验依据三角函数定义和正切曲线分析，由正切值求角的思维过程.发展数学直观素养.

总结

已知三角函数值或值的范围，求角或角的范围这类问题，可以借助单位圆中，随着角终边的旋转，三角函数值呈现的变化规律，来分析求解，也可以借助三角函数图像来分析求解，这两种途径都以三角函数定义为基础.求解过程中，运用了数与形之间的对应和统一的思想，以及整体求解的方法，通常先求一个周期内，满足所给条件的角，再依据周期性，求得定义域内所有解.

对整节课形成知识、方法、思想方面的认识.与已有知识、方法、思想结构建立联系.

作业

1.求解满足下列条件时,角的取值集合.

(1);           (2); 

(3);             (4).

2.求解满足下列条件时,角的取值集合.

(1);

(2);

(3);

(4).

3.求解满足下列条件时,角的取值集合.

(1)

(2)

运用本节课学的知识方法，解决问题，巩固所学.促进内化.