2020-2021学年北京市昌平区九年级（上）期末数学试卷

这是一份2020-2021学年北京市昌平区九年级（上）期末数学试卷，共1页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
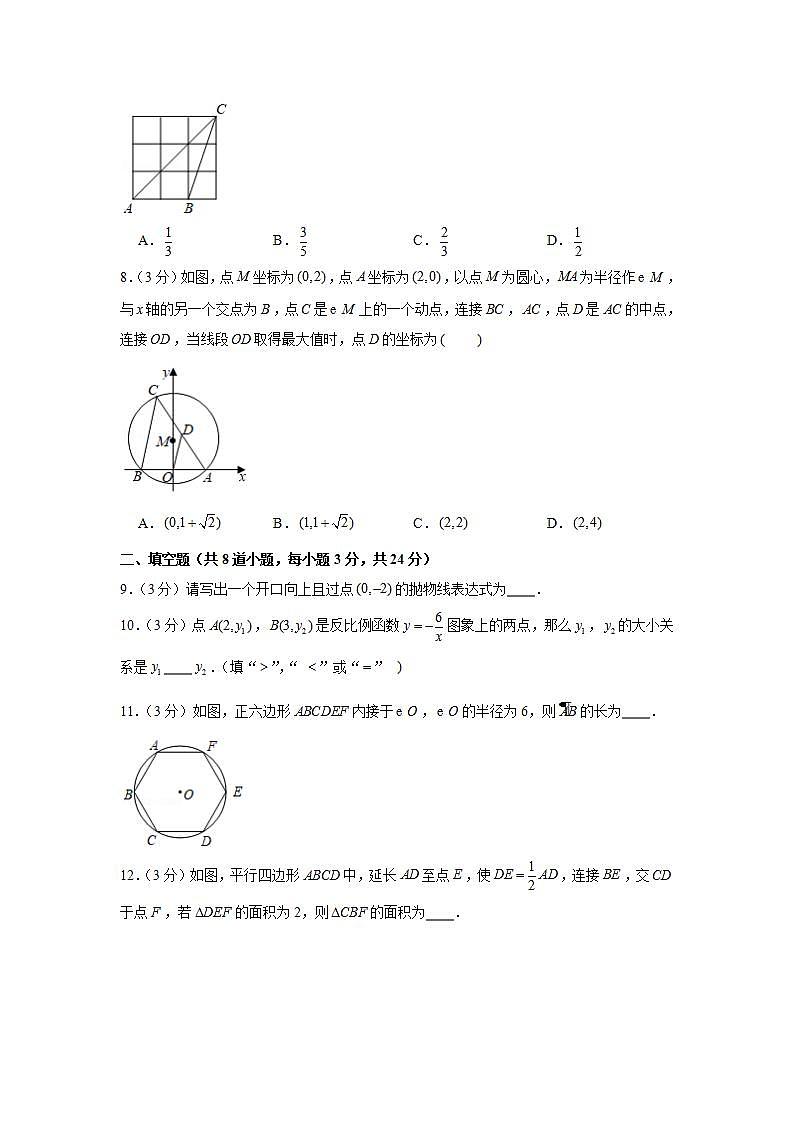
2020-2021学年北京市昌平区九年级（上）期末数学试卷一、选择题（共8道小题，每小题3分，共24分）下列各题均有四个选项，其中只有一个是符合题意的．1．（3分）如图，以点为圆心，以下列选项中的线段的长为半径作圆，所得的圆与直线相切的是　　A． B． C． D．2．（3分）如果，那么下列比例式中正确的是　　A． B． C． D．3．（3分）抛物线的顶点坐标是　　A． B． C． D．4．（3分）如图，是的直径，是的弦，如果，那么等于　　A． B． C． D．5．（3分）已知二次函数，若点和在此函数图象上，则与的大小关系是　　A． B． C． D．无法确定6．（3分）小英家在学校的北偏东40度的位置上，那么学校在小英家的方向是　　A．南偏东40度 B．南偏西40度 C．北偏东50度 D．北偏西50度7．（3分）如图，的顶点都在正方形网格的格点上，则的值为　　A． B． C． D．8．（3分）如图，点坐标为，点坐标为，以点为圆心，为半径作，与轴的另一个交点为，点是上的一个动点，连接，，点是的中点，连接，当线段取得最大值时，点的坐标为　　A． B． C． D．二、填空题（共8道小题，每小题3分，共24分）9．（3分）请写出一个开口向上且过点的抛物线表达式为　　．10．（3分）点，是反比例函数图象上的两点，那么，的大小关系是　　．（填“”，“ ”或“” 11．（3分）如图，正六边形内接于，的半径为6，则的长为　　．12．（3分）如图，平行四边形中，延长至点，使，连接，交于点，若的面积为2，则的面积为　　．13．（3分）如图，是的直径，弦，垂足为点，，，则　　，的半径为　　．14．（3分）如图，是的内切圆，切点分别为，，，已知，连接，，，，则　　，　　．15．（3分）二次函数图象上部分点的横坐标，纵坐标的对应值如下表：01204664则这个二次函数图像的对称轴为直线　　，　　．16．（3分）抛物线交轴于点和（点在点左侧），抛物线的顶点为，下列四个结论：①抛物线过点；②当时，是等腰直角三角形；③；④抛物线上有两点，和，，若，且，则．其中结论正确的序号是　　．三、解答题（共4道小题，每小题5分，共20分）17．（5分）计算：．18．（5分）如图，平分，．（1）求证：；（2）若，，求的长．19．（5分）已知二次函数．（1）写出该二次函数图象的对称轴及顶点坐标，再描点画图；（2）结合函数图象，直接写出时的取值范围．20．（5分）下面是小东设计的“过圆外一点作这个圆的切线”的尺规作图过程．已知：及外一点．求作：直线和直线，使切于点，切于点．作法：如图，①作射线，与交于点和点；②以点为圆心，以为半径作；③以点为圆心，以的直径为半径作圆，与交于点和点，连接和，分别与交于点和点；④作直线和直线．所以直线和就是所求作的直线．（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明．证明：连接和，，，点是的中点．，于点　　（填推理的依据）．同理于点．，为的半径，，是的切线．　　（填推理的依据）．四、解答题（共2道小题，21题5分，22题6分，共11分）21．（5分）某校九年级数学兴趣小组的同学进行社会实践活动时，想利用所学的解直角三角形的知识测昌平中心公园的仿古建筑“弘文阁” 的高度．他们先在点处用高1.5米的测角仪测得“弘文阁”顶的仰角为，然后向“弘文阁”的方向前进到达处，在点处测得“弘文阁”顶的仰角为．求“弘文阁” 的高（结果精确到，参考数据：，，．22．（6分）如图，为的直径，点，是上的点，平分，过点作的垂线，垂足为点．（1）求证：是的切线；（2）延长交的延长线于点，若半径的长为3，，求的长．五、解答题（共3道小题，每小题7分，共21分）23．（7分）在平面直角坐标系中，抛物线与轴交于点，将点向右平移2个单位长度，得到点，点在抛物线上．（1）①直接写出抛物线的对称轴是　　；②用含的代数式表示；（2）横、纵坐标都是整数的点叫做整点．若抛物线与轴交于、两点，该抛物线在、之间的部分与线段所围成的区域（不包括边界）恰有七个整点，结合函数图象，求的取值范围．24．（7分）在中，，，点是线段上的动点，作射线，点关于射线的对称点为，作直线，交射线于点．连接，．（1）依题意补全图形，直接写出的度数；（2）用等式表示线段，，之间的数量关系，并证明．25．（7分）在平面直角坐标系中，给出如下定义：若点在图形上，点在图形上，如果两点间的距离有最小值，那么称这个最小值为图形，的“近距离”，记为．特别地，当图形与图形有公共点时，．已知，，，．（1）（点，点　　，（点，线段　　；（2）半径为，①当时，求与正方形的“近距离” ；②若，则　　．（3）为轴上一点，的半径为1，与正方形的“近距离” ，请直接写出圆心的横坐标的取值范围．
2020-2021学年北京市昌平区九年级（上）期末数学试卷参考答案与试题解析一、选择题（共8道小题，每小题3分，共24分）下列各题均有四个选项，其中只有一个是符合题意的．1．（3分）如图，以点为圆心，以下列选项中的线段的长为半径作圆，所得的圆与直线相切的是　　A． B． C． D．【解答】解：于，以点为圆心，为半径的圆与直线相切．故选：．2．（3分）如果，那么下列比例式中正确的是　　A． B． C． D．【解答】解：、由比例的性质，得与不一致，故不符合题意；、由比例的性质，得与不一致，故不符合题意；、由比例的性质，得与不一致，故不符合题意；、由比例的性质，得与一致，故符合题意；故选：．3．（3分）抛物线的顶点坐标是　　A． B． C． D．【解答】解：，此函数的顶点坐标为，故选：．4．（3分）如图，是的直径，是的弦，如果，那么等于　　A． B． C． D．【解答】解：是的直径，，，，，故选：．5．（3分）已知二次函数，若点和在此函数图象上，则与的大小关系是　　A． B． C． D．无法确定【解答】解：点、是二次函数图象上的两点，，．．故选：．6．（3分）小英家在学校的北偏东40度的位置上，那么学校在小英家的方向是　　A．南偏东40度 B．南偏西40度 C．北偏东50度 D．北偏西50度【解答】解：小英家位于学校的东偏北，那么学校位于小英家的西偏南；故选：．7．（3分）如图，的顶点都在正方形网格的格点上，则的值为　　A． B． C． D．【解答】解：如图，连接．在中，，，，，故选：．8．（3分）如图，点坐标为，点坐标为，以点为圆心，为半径作，与轴的另一个交点为，点是上的一个动点，连接，，点是的中点，连接，当线段取得最大值时，点的坐标为　　A． B． C． D．【解答】解：，，，，，当取得最大值时，线段取得最大值，如图，为直径，，轴，，，，，是等腰直角三角形，，的坐标为，故选：．二、填空题（共8道小题，每小题3分，共24分）9．（3分）请写出一个开口向上且过点的抛物线表达式为　　．【解答】解：设抛物线的解析式为，把代入得，所以满足条件的抛物线解析式为．故答案为．10．（3分）点，是反比例函数图象上的两点，那么，的大小关系是　　．（填“”，“ ”或“” 【解答】解点，是反比例函数图象上的两点，，，．故答案为．11．（3分）如图，正六边形内接于，的半径为6，则的长为　　．【解答】解：如图，连接，．由题意，，的长．故答案为：．12．（3分）如图，平行四边形中，延长至点，使，连接，交于点，若的面积为2，则的面积为　8　．【解答】解：设，由，则：，四边形是平行四边形，，，，则，，的面积为2，则的面积为8，故答案为8．13．（3分）如图，是的直径，弦，垂足为点，，，则　8　，的半径为　　．【解答】解：连接，为的直径，弦于，，设的半径为，则，，即解得，故答案为8，10．14．（3分）如图，是的内切圆，切点分别为，，，已知，连接，，，，则　110　，　　．【解答】解：如图，连接和，是的内切圆，切点分别为，，，，，平分，，，，，，，．故答案为：110，70．15．（3分）二次函数图象上部分点的横坐标，纵坐标的对应值如下表：01204664则这个二次函数图像的对称轴为直线　　，　　．【解答】解：，；，，抛物线的对称轴为直线，抛物线过点，，抛物线过点和，，解得：，二次函数的表达式为：，把代入得，，解得或，，，故答案为，4．16．（3分）抛物线交轴于点和（点在点左侧），抛物线的顶点为，下列四个结论：①抛物线过点；②当时，是等腰直角三角形；③；④抛物线上有两点，和，，若，且，则．其中结论正确的序号是　①②④　．【解答】解：①把代入得，，抛物线过点，故①正确；②当时，抛物线与轴的两个交点坐标分别为、，对称轴为，是等腰直角三角形，故②正确；③抛物线交轴于点和（点在点左侧），、是方程的两个根，，故③错误；④观察二次函数图象可知：当，且，则．故④正确．故答案为：①②④．三、解答题（共4道小题，每小题5分，共20分）17．（5分）计算：．【解答】解：．18．（5分）如图，平分，．（1）求证：；（2）若，，求的长．【解答】（1）解：分，．，； （2），．，，．19．（5分）已知二次函数．（1）写出该二次函数图象的对称轴及顶点坐标，再描点画图；（2）结合函数图象，直接写出时的取值范围．【解答】解：（1），该函数的对称轴为直线，顶点坐标为，当时，，，当时，，时，，函数图象如右图所示；（2）由图象可得，当时，的取值范围是．20．（5分）下面是小东设计的“过圆外一点作这个圆的切线”的尺规作图过程．已知：及外一点．求作：直线和直线，使切于点，切于点．作法：如图，①作射线，与交于点和点；②以点为圆心，以为半径作；③以点为圆心，以的直径为半径作圆，与交于点和点，连接和，分别与交于点和点；④作直线和直线．所以直线和就是所求作的直线．（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明．证明：连接和，，，点是的中点．，于点　（三线合一）　（填推理的依据）．同理于点．，为的半径，，是的切线．　　（填推理的依据）．【解答】解：（1）补全图形如图： （2）证明：连接和，，，点是的中点，．于点（三线合一），同理于点，，为的半径，，是的切线．（经过半径的外端，和半径垂直的直线是圆的切线）．故答案为：（三线合一），经过半径的外端，和半径垂直的直线是圆的切线．四、解答题（共2道小题，21题5分，22题6分，共11分）21．（5分）某校九年级数学兴趣小组的同学进行社会实践活动时，想利用所学的解直角三角形的知识测昌平中心公园的仿古建筑“弘文阁” 的高度．他们先在点处用高1.5米的测角仪测得“弘文阁”顶的仰角为，然后向“弘文阁”的方向前进到达处，在点处测得“弘文阁”顶的仰角为．求“弘文阁” 的高（结果精确到，参考数据：，，．【解答】解：由题可知：，，，．．在中，，，．在中，，，．，，．．．答：“弘文阁” 高约．22．（6分）如图，为的直径，点，是上的点，平分，过点作的垂线，垂足为点．（1）求证：是的切线；（2）延长交的延长线于点，若半径的长为3，，求的长．【解答】（1）证明：连接．平分，，，，，，，，是半径，是的切线．（2）解：连接，交于点．是的直径，，，，四边形是矩形，，，，在中，，，设，，，解得，负值舍去，．五、解答题（共3道小题，每小题7分，共21分）23．（7分）在平面直角坐标系中，抛物线与轴交于点，将点向右平移2个单位长度，得到点，点在抛物线上．（1）①直接写出抛物线的对称轴是　直线　；②用含的代数式表示；（2）横、纵坐标都是整数的点叫做整点．若抛物线与轴交于、两点，该抛物线在、之间的部分与线段所围成的区域（不包括边界）恰有七个整点，结合函数图象，求的取值范围．【解答】解：（1）①与关于对称轴对称，抛物线对称轴为直线，故答案为直线；②抛物线与轴交于点，，点向右平移2个单位长度，得到点，点在抛物线上，，．（2）由题可知：，，，①若时，如图1，在、之间的部分与线段所围成的区域（不包括边界）内的七个整点为，，，，，，，时，，顶点为，，；②若时，如图2，在、之间的部分与线段所围成的区域（不包括边界）内的七个整点为，，，，，，， 当时，，恰有7个整数点，，综上，的取值范围是或．24．（7分）在中，，，点是线段上的动点，作射线，点关于射线的对称点为，作直线，交射线于点．连接，．（1）依题意补全图形，直接写出的度数；（2）用等式表示线段，，之间的数量关系，并证明．【解答】解：（1）补图如图，，如图，延长至点使，由对称可知：，，，，，；，，，在和中，，，，，，即，；（2），延长至点使，由对称可知：，，，，，；，，，在和中，，，，，，即，；，即，．25．（7分）在平面直角坐标系中，给出如下定义：若点在图形上，点在图形上，如果两点间的距离有最小值，那么称这个最小值为图形，的“近距离”，记为．特别地，当图形与图形有公共点时，．已知，，，．（1）（点，点　8　，（点，线段　　；（2）半径为，①当时，求与正方形的“近距离” ；②若，则　　．（3）为轴上一点，的半径为1，与正方形的“近距离” ，请直接写出圆心的横坐标的取值范围．【解答】解：（1）如图1中，观察图象可知（点，点，（点，线段．故答案为：8，4． （2）①如图2中，过点作于，交于．，，，，，，与正方形的“近距离” ． ②当时，当在正方形内部时，，，当正方形在的内部时，，综上所述，满足条件的的值为或5．故答案为：或5． （3）如图3中，当在的左侧时，过点作于，交于．当时，，，，当在的右侧时，时，，观察图象可知，满足条件的点的坐标为：．根据对称性可知，也满足条件．综上所述，的取值范围为：或．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2021/12/8 12:36:55；用户：初中数学1；邮箱：jse032@xyh.com；学号：39024122