高中数学人教版（中职）基础模块上册第二章不等式2.2 不等式的解法评课课件ppt

展开

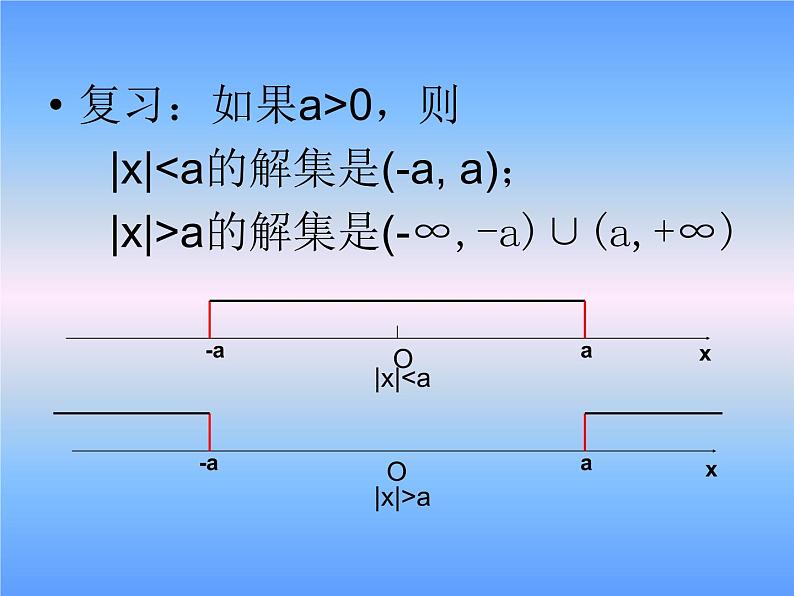
这是一份高中数学人教版（中职）基础模块上册第二章不等式2.2 不等式的解法评课课件ppt，共36页。PPT课件主要包含了x-a＜x＜a，x∈Rx≠0，-c≤ax+b≤c，答案［26］，类题试解等内容，欢迎下载使用。

复习：如果a>0，则 |x|a的解集是(-∞,-a)∪(a,+∞)
1.含绝对值的不等式|x|a的解集.
{x|x＞a或x＜-a}
2.|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法.(1)|ax+b|≤c⇔____________.(2)|ax+b|≥c⇔__________________.
ax+b≥c或ax+b≤-c
1.不等式|x－1|＜2的解集是_____.【解析】由|x－1|＜2得－2＜x－1＜2，解得－1＜x＜3.答案：(－1,3)
2.不等式|4－3x|≥2的解集是_____.【解析】|4－3x|≥2⇔|3x－4|≥2⇔3x－4≤－2或3x－4≥2，解得或x≥2.答案：
解含绝对值不等式的核心任务解含绝对值不等式的核心任务是：去绝对值，将不等式恒等变形为不含绝对值的常规不等式，然后利用已经掌握的解题方法求解；注意不可盲目平方去绝对值符号.
类型一简单绝对值不等式的解法 1.不等式的解集是_____.2．不等式的解集为______.
【拓展提升】绝对值不等式的常见类型及其解法(1)形如|f(x)|a(a∈R)型不等式. 此类不等式的简单解法是等价转化法，即 ①当a>0时，|f(x)|a⇔f(x)>a或f(x)<-a. ②当a=0时，|f(x)|a⇔f(x)≠0.
③当a<0时，|f(x)|a⇔f(x)有意义即可.
(2)形如|f(x)|<|g(x)|型不等式. 此类问题的简单解法是利用平方法，即 |f(x)|<|g(x)|⇔［f(x)］2<［g(x)］2 ⇔［f(x)+g(x)］［f(x)-g(x)］<0.
(3)形如|f(x)|g(x)型不等式. 此类不等式的简单解法是等价转化法，即 ①|f(x)|g(x)⇔f(x)>g(x)或f(x)<-g(x)(其中g(x)可正也可负). 若此类问题用分类讨论法来解决，就显得较复杂.
(4)形如a<|f(x)|a>0)型不等式. 此类问题的简单解法是利用等价转化法，即 a<|f(x)|f(x)型不等式. 此类问题的简单解法是利用绝对值的定义，即 |f(x)|f(x)⇔f(x)<0.
类型二含多个绝对值不等式的解法【典型例题】1.不等式|x－1|＞|x－2|的解集为______.2.不等式|x+1|+|x-1|≥3的解集为______.
【变式练习】若将题1中的不等式改为求它的解集.
探究提示：1.题1中可采用不等式两边同时平方的方式去掉绝对值符号.2.解决题2的关键是理解绝对值的几何意义.【解析】1.|x－1|＞|x－2|⇔(x－1)2＞(x－2)2所以原不等式的解集为答案：
2.方法一：如图,设数轴上与-1,1对应的点分别为A,B,那么A,B两点间的距离为2,因此区间［-1,1］上的数都不是不等式的解.设在A点左侧有一点A1到A,B两点的距离和为3,A1对应数轴上的x.所以-1-x+1-x=3,得同理设B点右侧有一点B1到A,B两点的距离和为3，B1对应数轴上的x,所以x-1+x-(-1)=3.所以
从数轴上可看到，点A1，B1之间的点到A，B的距离之和都小于3；点A1的左边或点B1的右边的任何点到A，B的距离之和都大于3，所以原不等式的解集是
方法二：当x≤-1时,原不等式可以化为-(x+1)-(x-1)≥3,解得当-1＜x＜1时,原不等式可以化为x+1-(x-1)≥3,即2≥3.不成立,无解.当x≥1时,原不等式可以化为x+1+x-1≥3.所以综上,可知原不等式的解集为
方法三：将原不等式转化为|x+1|+|x-1|-3≥0.构造函数y=|x+1|+|x-1|-3,即作出函数的图象(如图).函数的零点是
从图象可知当或时,y≥0.即|x+1|+|x-1|-3≥0.所以原不等式的解集为答案：
3.|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的解法.(1)利用绝对值不等式的几何意义求解，体现数形结合思想,理解绝对值的几何意义,给绝对值不等式以准确的几何解释.(2)以绝对值的零点为分界点,将数轴分为几个区间,利用“零点分段法”求解，体现分类讨论的思想.确定各个绝对值符号内多项式的_______性，进而去掉绝对值符号.(3)通过构造函数，利用函数的图象求解，体现了函数与方程的思想.正确求出函数的_____并画出函数图象(有时需要考查函数的增减性)是关键.
【互动探究】若将题1中的不等式改为求它的解集.【解析】又2－x≥0，所以x≤2.所以原不等式的解集为【误区警示】本题易忽视隐含条件2-x≥0而致误.
【拓展提升】|x-a|+|x-b|≥c,|x-a|+|x-b|≤c(c>0)型不等式的解法(1)|x-a|+|x-b|≥c,|x-a|+|x-b|≤c(c>0)型不等式有三种解法：分区间(分类)讨论法\,图象法和几何法.分区间讨论的方法具有普遍性,但较麻烦;几何法和图象法直观,但只适用于数据较简单的情况.
(2)分区间(分类)讨论的关键在于对绝对值代数意义的理解,即也即x∈R.x为非负数时,｜x｜为x;x为负数时,｜x｜为-x,即x的相反数.
(3)｜x-a｜+｜x-b｜≥c,｜x-a｜+｜x-b｜≤c(c>0)型不等式的图象解法和画出函数f(x)=｜x-a｜+｜x-b｜-c的图象是密切相关的,其图象是折线,正确地画出其图象的关键是写出f(x)的分段表达式.不妨设a 其他类型的绝对值不等式【典型例题】1.不等式｜2x-3｜＜3x+1的解集是_____.2.设函数f(x)=|x-1|+|x-a|,如果对任意x∈R,f(x)≥2,则a的取值范围是_______.3.解不等式：|x2－3|＜2x.
【解析】1.|2x-3|<3x+1,由题意知3x+1>0,原不等式转化为-(3x+1)<2x-3<3x+1.以上不等式等价于所以原不等式的解集为答案：
2.若a=1,则f(x)=2|x-1|,不满足题设条件.若a<1,则 ⇒f(x)的最小值为1-a.若a>1,则 ⇒f(x)的最小值为a-1.综上可知，所求a的取值范围是(-∞,-1］∪［3,+∞).答案：(-∞,-1］∪［3,+∞)
3. 因为|x2－3|＜2x，所以x＞0，所以|x2－3|＜2x⇔－2x＜x2－3＜2x⇔解不等式组得
【拓展提升】含参数的不等式问题分类及解题策略(1)一类要对参数进行讨论，另一类对参数并没有进行讨论，而是去绝对值时对变量进行讨论，得到两个不等式组，最后把两不等式组的解集合并，即得该不等式的解集.(2)解绝对值不等式的基本思想是想方设法去掉绝对值符号，去绝对值符号的常用手段有以下几种：形如｜f(x)｜≤g(x)或｜f(x)｜>g(x)的求解方法：(ⅰ)根据实数的绝对值的意义分类讨论，
即(ⅱ)根据公式：|x|0);｜f(x)｜a⇔x>a或x<-a(a∈R且a≥0);｜f(x)｜>g(x)⇔f(x)>g(x)或f(x)<-g(x).(ⅲ)根据|a|2=a2(a∈R)，若不等式两边非负,可在不等式两边同时平方,如｜f(x)｜≤｜g(x)｜⇔f2(x)≤g2(x).
【规范解答】含参数的绝对值不等式的解法【规范解答】因为a∈R,故分以下两种情况讨论：(1)当a+1≤0①,即a≤-1时，
原不等式无解，即不等式的解集为∅
(2)当a+1>0,即a>-1时，……………………………………………………6分原不等式可变为-a-1<2x+3-1时，原不等式的解集为 ②当a≤-1时，原不等式的解集为∅. ………………………12分
【防范措施】含参数的绝对值不等式解含参数的绝对值不等式的题型，容易忽略对参数的符号进行讨论，如本例需对a+1的符号进行讨论，否则易导致错误结果.
1.解关于x的不等式：|x2-a|0时，原不等式等价于-a0时，原不等式的解集为
2.若不等式|ax+2|＜6的解集为(－1,2)，则实数a=______.
2.若不等式|ax+2|＜6的解集为(－1,2)，则实数a=______.【解析】由|ax+2|＜6得－8＜ax＜4,当a＞0时，因为不等式的解集为(－1,2)，所以解得两值相矛盾.当a＜0时，则解得a=－4.综上得，a=－4.答案：－4
【点评】解绝对值不等式的关键在于去掉绝对值符号，处理的方法通常是定义、平方、几何意义等方法．对含多个绝对值符号的不等式一般利用”零点分割”法分段讨论．本题是绝对值不等式的简单应用．利用去绝对值符号的两种方法，可以解含有绝对值符号的不等式，也可以转化为求最值或求参数范围．下面的变式训练是含参数的绝对值不等式的求解问题

相关课件更多