七年级上册3 余角和补角图文ppt课件

这是一份七年级上册3 余角和补角图文ppt课件，共15页。PPT课件主要包含了比萨斜塔，新课引入，余角和补角的概念，新课讲解，随堂即练，°37′，余角和补角的性质，∠2180°－∠1，∠3180°－∠1，类似的可以得到等内容，欢迎下载使用。
1.了解余角、补角的概念；2.掌握余角和补角的形质；（重点）3. 能用余角与补角解决一些问题.（难点）
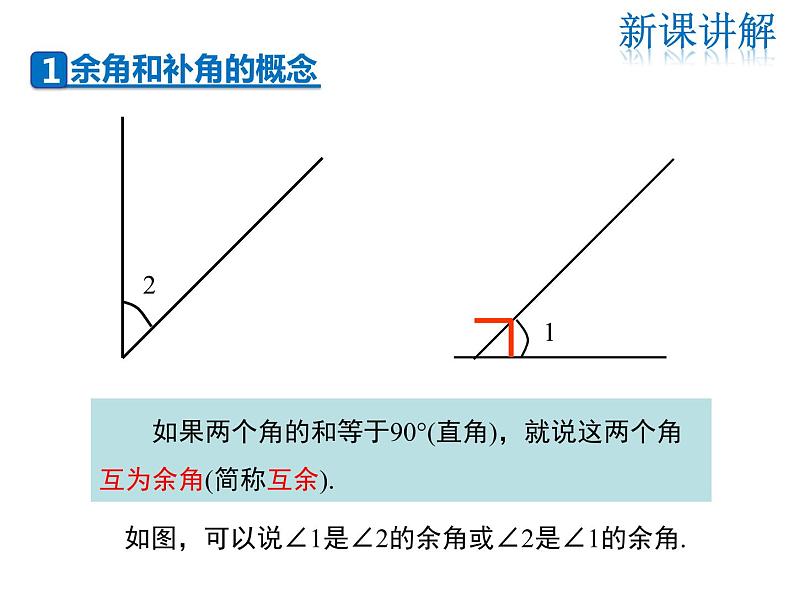
想一想∠1与∠2有什么关系？
想一想∠1与∠3有什么关系？
如果两个角的和等于90°(直角)，就说这两个角互为余角(简称互余).
如图，可以说∠1是∠2的余角或∠2是∠1的余角.
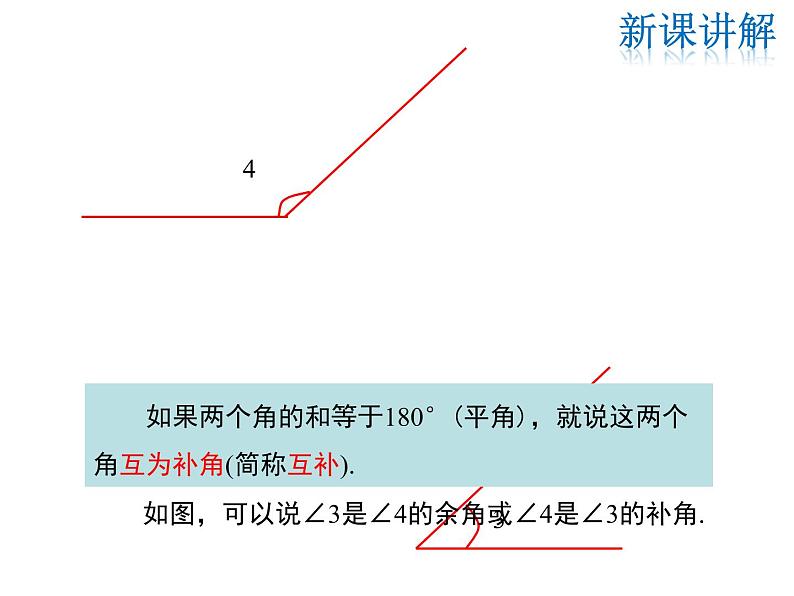
如果两个角的和等于180°(平角)，就说这两个角互为补角(简称互补).
如图，可以说∠3是∠4的余角或∠4是∠3的补角.
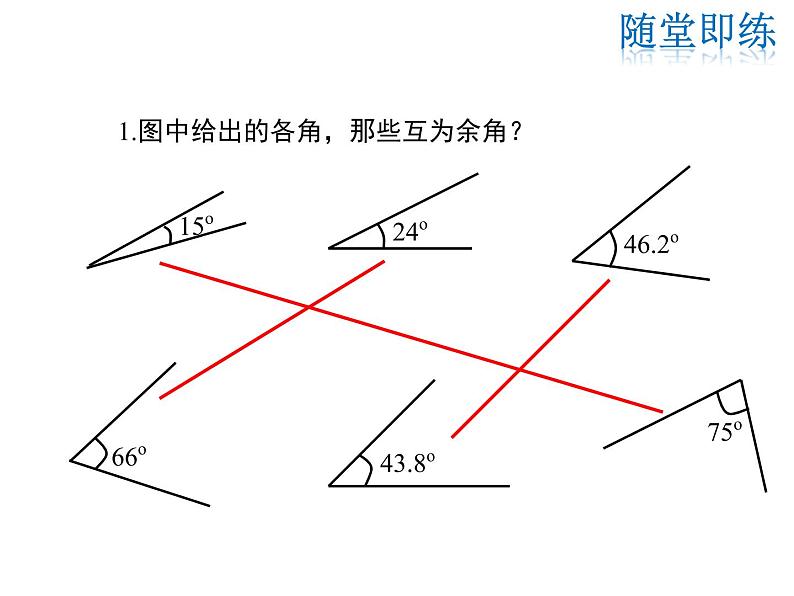
1.图中给出的各角，那些互为余角？
2.图中给出的各角，那些互为补角？
例1 若一个角的补角等于它的余角的4 倍，求这个角的度数.
解：设这个角是x°，则它的补角是(180°－x°),余角是(90°－x°) . 根据题意，得180°－x°= 4 (90°－x°) 解得 x=60答：这个角的度数是60 °.
观察可得结论： 同一个锐角的补角比它的余角大________.
∠1与∠2，∠3都互为补角，∠2与∠3的大小有什么关系？
同角(等角)的补角相等
同角(等角)的余角相等
例2 如图，点A，O，B在同一直线上，射线OD和射线OE分别平分∠AOC和∠BOC，图中哪些角互为余角？
解：因为点A，O，B在同一直线上，所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC，所以∠COD+∠COE= ∠AOC+ ∠BOC = (∠AOC+∠BOC)=90°.
所以∠COD和∠COE互为余角，
同理∠AOD和∠BOE，∠AOD和∠COE，∠AOD和∠BOE也互为余角.
2.如图, ∠COD= ∠EOD=90°, C、O、E在一条直线上, 且∠2= ∠4, 请说出∠1与∠3之间的关系?并试着说明理由?
解：∠1与∠3相等(等角的余角相等).