北师大版第三章 三角恒等变换3二倍角的三角函数课文内容ppt课件

这是一份北师大版第三章 三角恒等变换3二倍角的三角函数课文内容ppt课件，共42页。PPT课件主要包含了必备知识·自主学习，二倍角公式及其变形，关键能力·合作学习，课堂检测·素养达标等内容，欢迎下载使用。

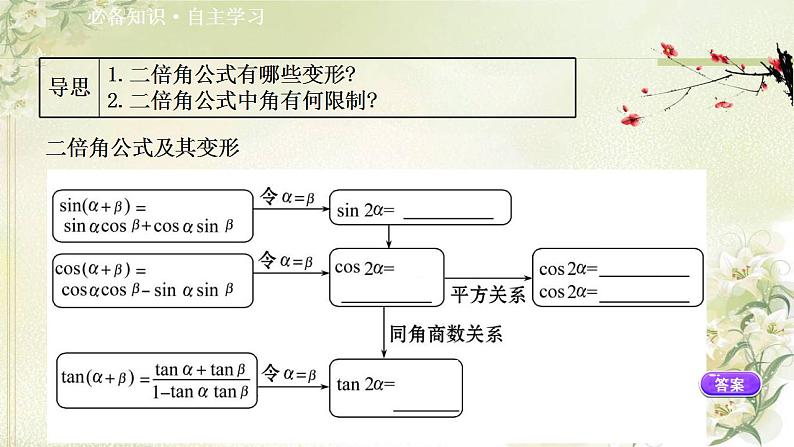
【思考】1.如何理解公式中的倍角?提示:公式中的“倍角”是相对的,对于两个角的比值等于2的情况都成立,如6α是3α的2倍,3α是 的2倍……
2.二倍角公式有哪些变形形式?提示:(1)1±sin 2α=(sin α±cs α)2;(2)1+cs 2α=2cs2α,1-cs 2α=2sin2α(升幂降角公式);(3)cs2α= ,sin2α= (降幂升角公式).
【基础小测】1.辨析记忆(对的打“√”,错的打“×”)(1)对任意α∈R,总有sin 2α=2sin α.(　　)(2)对任意α∈R,总有cs 2α=1-2cs2α.(　　)(3)对任意α∈R,总有tan 2α= .(　　)(4)sin 22°30′cs 22°30′= .(　　)(5)sin2α= .(　　)
提示:(1)×.sin 2α=2sin αcs α.(2)×.cs 2α=2cs2α-1.(3)×.(4)√.sin 22°30′cs 22°30′= ×2sin 22°30′cs 22°30′= sin 45°= .(5)√. = =sin2α.
2.函数 的最小正周期为(　　)A. B. C.πD.2π【解析】选C.由已知得f(x)= 所以f(x)的最小正周期T= =π.
3.(教材二次开发:例题改编)若cs α= 求sin 2α,cs 2α,tan 2α的值.【解析】因为cs α= ,0<α< ,所以sin α= .所以sin 2α=2sin αcs α= tan 2α=
类型一　条件求值(逻辑推理)【题组训练】1.若 则sin 2α=(　　) 2.(2020·合肥高一检测)已知角α的顶点在坐标原点,始边与x轴正半轴重合,终边经过点P(- ,1),则cs 2α=(　　) 3.已知α∈ ,且sin 2α=sin ,求α.
【解析】1.选D. sin 2α,即sin 2α=- .2.选B. 因为角α的顶点在坐标原点,始边与x轴正半轴重合,终边经过点P(- ,1),所以cs α= 所以cs 2α=2cs2α-1= .
3.因为sin 2α= sin =-cs ,所以原方程可化为1-2cs2 =-cs ,解得cs =1或cs =- .因为α∈ ,所以 故α+ =0或α+ = ,即α=- 或α= .
【解题策略】解决条件求值问题的方法条件求值问题,注意寻找已知式与未知式之间的联系,有两个观察方向:(1)有方向地将已知式或未知式化简,使关系明朗化.(2)寻找角之间的关系,看是否适合相关公式的使用,注意常见角的变换和角之间的二倍关系.
【补偿训练】已知sin = ,0【解析】因为0类型二　二倍角公式的变形(数学运算)【典例】已知函数f(x)=2cs2x-sin2x+2,则(　　)A. f(x)的最小正周期为π,最大值为3B. f(x)的最小正周期为π,最大值为4C. f(x)的最小正周期为2π,最大值为3D. f(x)的最小正周期为2π,最大值为4
【思路导引】利用二倍角公式的变形公式整理可得f(x)= 然后应用余弦型函数的性质得到相关的量.【解析】选B.根据题意得,f(x)=2cs2x-sin2x+2= 所以f(x)的最小正周期为T= =π,且最大值为f(x)max= =4.
【解题策略】关于二倍角公式的变形使用(1)逆用:如果式子符合或变形后符合逆用的特点,则可以逆用二倍角公式,如sin αcs α, 等.(2)变形:常用的二倍角的变形有降幂公式,1±cs 2α等.
【跟踪训练】(1)已知sin 2α=- ,α∈ ,则sin α+cs α=(　　)A. B.- C.- D. (2)若 ,则sin 2α=______. 
【解析】(1)选A.因为α∈ ,所以sin α+cs α>0,所以(sin α+cs α)2=1+sin 2α= ,所以sin α+cs α= .(2)因为 ,所以 ,解得sin α-cs α=- ,两边平方得1-sin 2α= ,所以sin 2α= .答案:
类型三　二倍角公式的综合应用(逻辑推理)　角度1　化简求值 【典例】化简求值:cs 20°cs 40°cs 60°cs 80°=________. 【思路导引】观察角20°,40°,80°之间的二倍关系,可以联想到利用二倍角公式,采用添项的方法求解.
【解析】原式= 答案:
【变式探究】化简: =________. 【解析】 答案:tan θ
角度2　三角函数中的应用 【典例】设常数a∈R,函数f(x)=asin 2x+2cs2x.(1)若f(x)为偶函数,求a的值.(2)若f = +1,求方程f(x)=1- 在区间[-π,π]上的解.【思路导引】利用二倍角公式和两角和的正弦公式求解.
【解析】(1)因为f(x)为偶函数,而f(x)=asin 2x+2cs2x=asin 2x+cs 2x+1,所以f(-x)=asin(-2x)+cs(-2x)+1=-asin 2x+cs 2x+1=f(x),故a=0.(2)因为f =asin +cs +1=a+1= +1,所以a= ,故f(x)= sin 2x+2cs2x= sin 2x+cs 2x+1=2sin +1,当x∈[-π,π]时,2x+ ∈ ,令f(x)=1- ,即2sin +1=1- ,化简得sin =- .因为2x+ ∈ ,
所以2x+ =- π,- , π, π,解得x=
【解题策略】应用公式解决三角函数综合问题的三个步骤
提醒:根据需要有时也将三角函数式化为f(x)=Acs(ωx+φ)+k的形式, x的系数一般为正数.
【题组训练】1.（2020·全国Ⅰ卷）已知α∈(0,π)，且3cs 2α-8cs α=5，则sin α=（ ）【解析】选A.3cs 2α-8cs α=5，得6cs2α-8cs α-8=0，即3cs2α-4cs α-4=0，解得cs α=- 或cs α=2（舍去），又因为α∈(0,π),所以sin
2.求值:tan 15°+ =________. 【解析】原式= 答案:4
3.已知函数f(x)= (1)求函数f(x)的对称轴方程.(2)求函数f(x)在区间 上的最大值和最小值以及相应的x的值.
【解析】(1)由题意,函数 令 整理得x=kπ+ ,所以函数f(x)的对称轴方程为x=kπ+ .
(2)由(1)得: f(x)= 由于x∈ ,所以 则-1≤ 所以- ≤f(x)≤1,当x=- 时,函数的最小值为- .当x=0时,函数的最大值为1.
【补偿训练】已知向量a=(sin A,cs A),b=( ,-1),a·b=1,且A为锐角.(1)求角A的大小.(2)求函数f(x)=cs 2x+4cs Asin x(x∈R)的值域.
【解析】(1)由题意得a·b= sin A-cs A=1, 由A为锐角得 所以A= .(2)由(1)知cs A= ,所以f(x)=cs 2x+2sin x=1-2sin2x+2sin x= 因为x∈R,所以sin x∈[-1,1],
因此,当sin x= 时,f(x)有最大值 .当sin x=-1时,f(x)有最小值-3.所以所求函数f(x)的值域是 .
1.化简: =(　　)A.1　　　　　B.2　　　　　C. 　　　　　D.-1【解析】选B.
2.在△ABC中, 则cs 2A=(　　) 【解析】选A.在△ABC中, 则 所以cs2A=
3.(教材二次开发:习题改编)已知x∈ ,sin x=- ,则tan 2x=(　　) 【解析】选D.因为x∈ ,sin x=- ,所以cs x= tan x= 则tan 2x=
4.(2019·北京高考)函数f(x)=sin22x的最小正周期是________. 【解析】因为f(x)=sin22x= 所以最小正周期为T= 答案:
5.已知 (1)求tan α的值.(2)求 的值.【解析】(1)方法一:因为 所以tan α=