高中北师大版1.1利用函数性质判定方程解的存在课前预习ppt课件

这是一份高中北师大版1.1利用函数性质判定方程解的存在课前预习ppt课件，共15页。PPT课件主要包含了f0-6，f-414，f46，三巩固提高等内容，欢迎下载使用。
1.我们学过了一元一次方程、一元二次方程的解法，那么方程 x+1=0是否存在实数解？2.方程x2-x-6=0是否存在实数解？
3.方程3x-x2=0是否存在实数解？
§1.1利用函数性质判定方程解的存在
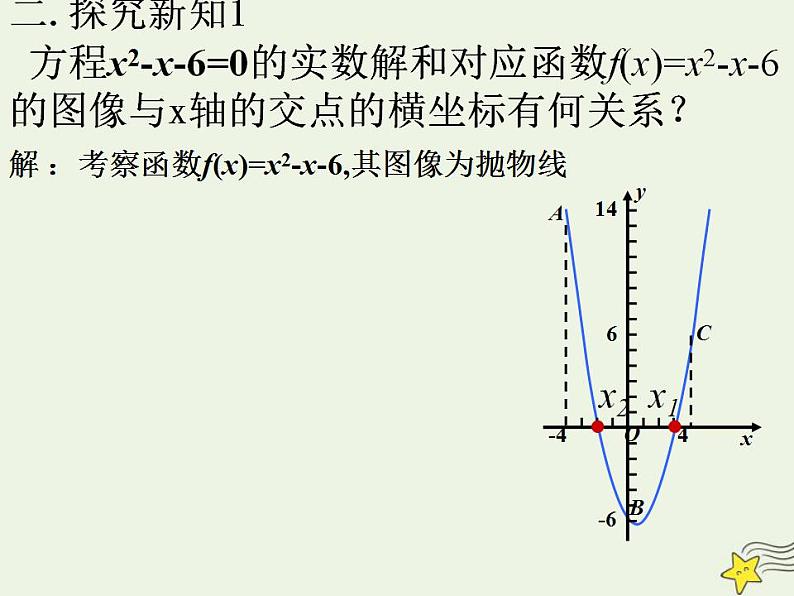
方程x2-x-6=0的实数解和对应函数f(x)=x2-x-6的图像与x轴的交点的横坐标有何关系？
解 ：考察函数f(x)=x2-x-6,其图像为抛物线
函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点.
③函数y=f(x) 的零点与对应方程f(x)=0的实数解的关系：函数y=f(x) 的零点就是方程f(x)=0的实数解
思考：①零点是点吗？ ②所有函数都有零点吗？
函数f(x)=x2-x-6满足什么条件存在零点？
容易算出 : f(0)0, f(-4)>0并且函数y=f(x)图像为连续曲线，因此，点B(0,-6)与点C(4,6)之间的那部分曲线必然穿过x轴，即在区间(0,4) 至少有一点x1，使f(x1)=0；同样，在区间(-4，0) 至少有一点x2，使f(x2)=0。而函数f(x)=x2-x-6的图像与x轴至多有两个交点所以函数f(x)=x2-x-6在(-4,0)、(0,4)内各有一零点
函数y=f(x) 满足什么条件存在零点？
（1）如图1，y=f(x)在闭区间[a,b]上，有f(a)·f(b)