北师大版4.5 多边形和圆的初步认识学案

多边形和圆的初步认识

学法指导

在具体情景中认识多边形、正多边形、圆和扇形，利用扇形与圆的关系求扇形的圆心角的度数

一.预学质疑（设疑猜想.主动探究）

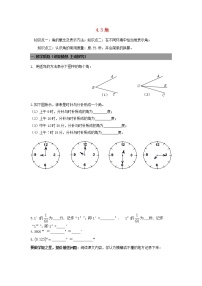
1.下边说法正确的是（）

A.各边相等的多边形一定是正多边形         B.各角相等的多边形一定是正多边形

C.正多边形各边都相等，各角也相等         D.等边三角形不是正多边形

2.从n边形一个顶点出发，共有_____条对角线，这些对角线把四边形分成_____个三角形。

3.一个扇形占整个圆周的15％，那么这个扇形的圆心角为________.

4.扇形圆心角为30°，若此扇形半径为1，那么此扇形面积是多少?

要做学疑之星，提价值性问题：阅读课文内容，你认为模糊或不懂的地方记录下来：

二.研学析疑（合作交流.解决问题）

【问题一】请仔细阅读课本P122，你能回答以下问题吗？

1.什么是多边形？

2.我们常见的图形哪些是多边形？

3.什么叫多边形的对角线？

4.找出右图中多边形的顶点，多边形的边，多边形的内角以及多边形的对角线。

【问题二】填写下表，你能从表格中的结果发现什么规律吗？你能用代数式把你发现的规律表示出来吗？

在平面内，各内角都相等.各边也都相等的多边形叫做           。如正三角形，正四边形（正方形），正五边形，正六边形，正八边形。 

【问题三】自读课本123页，并回答下列问题

1.什么样的图形叫做圆？

2.找出图1中的半径、圆弧、扇形和圆心角。     

3.会读写圆弧。

例1.将一个圆分割成三个扇形，使它们的圆心角的比为2：3：5，求这三个扇形的圆心角的度数。

【问题四】（1）将一个圆分成三个大小相同的扇形，你能算出它们的圆心角的度数吗？你知道每个扇形的面积和整个圆的面积的关系吗？与同伴进行交流

(2)画一个半径是3cm的圆，并在其中画一个圆心为120º的扇形，你会计算这个扇形的面积吗？与同伴交流。

三.导法展示(巩固升华.拓展思维)

1.若一个多边形从一个顶点出发最多可以引10条对角线，则它是（     ）

A.十三边形      B.十二边形       C.十一边形         D.十边形

2.下列说法不正确的是（     ）

A.各边相等的多边形是正多边形        B.等边三角形是正多边形

C.正多边形的各角必相等              D.各角相等的多边形不一定是正多边形

3.将一个圆分割成三个扇形，使它们的圆心角的比为1：3：4，求这三个扇形的圆心角的度数。

4.从一个三角形的某个顶点出发，分别连接这个顶点与其余各顶点，也可以把这个三角形分割成多少个三角形？四边形，五边形，六变形，边形呢？你又能找出什么规律呢？

四、小结反思（自主整理，归纳总结）

五、促评反思（反思评价、课外练习）

1.从一个十边形的某个顶点出发，分别连结这个点与其余各顶点，可以画出多少条对角线？

2.如图，把一个圆分成三个扇形，你能求出这三个扇形的圆心角吗？

3.半径为3的圆中，扇形AOB的面积是，请求出扇形AOB的圆心角的度数。