2020-2021学年第八章 立体几何初步本章综合与测试当堂达标检测题

这是一份2020-2021学年第八章 立体几何初步本章综合与测试当堂达标检测题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

章末综合测评(三)　立体几何初步
(满分：150分　时间：120分钟)
一、选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)
1．下面给出了四个条件：
①空间三个点；②一条直线和一个点；③和直线a都相交的两条直线；④两两相交的三条直线．
其中，能确定一个平面的条件有(　　)
A．3个　　　B．2个　　　C．1个　　　D．0个
D　[①当空间三点共线时不能确定一个平面；②点在直 线上时不能确定一个平面；③两直线若不平行也不相交时不能确定一个平面；④三条直线交于一点且不共面时不能确定一个平面． 故以上4个条件都不能确定一个平面．]
2．在长方体ABCD­A1B1C1D1中，异面直线AB，A1D1所成的角等于(　　)
A．30° B．45° C．60° D．90°
D　[由于AD∥A1D1，则∠BAD是异面直线AB，A1D1所成的角，很明显∠BAD＝90°．]
3．已知a，b，c是直线，则下面四个命题：
①若直线a，b异面，b，c异面，则a，c异面；
②若直线a，b相交，b，c相交，则a，c相交；
③若a∥b，则a，b与c所成的角相等．
其中真命题的个数为(　　)
A．0 B．3 C．2 D．1
D　[异面、相交关系在空间中不能传递，故①②错；根据等角定理，可知③正确．]
4．一个棱柱的侧面展开图是三个全等的矩形，矩形的长和宽分别为6 cm,4 cm，则该棱柱的侧面积为(　　)
A．24 cm2 B．36 cm2 C．72 cm2 D．84 cm2
C　[棱柱的侧面积S侧＝3×6×4＝72(cm2)．]
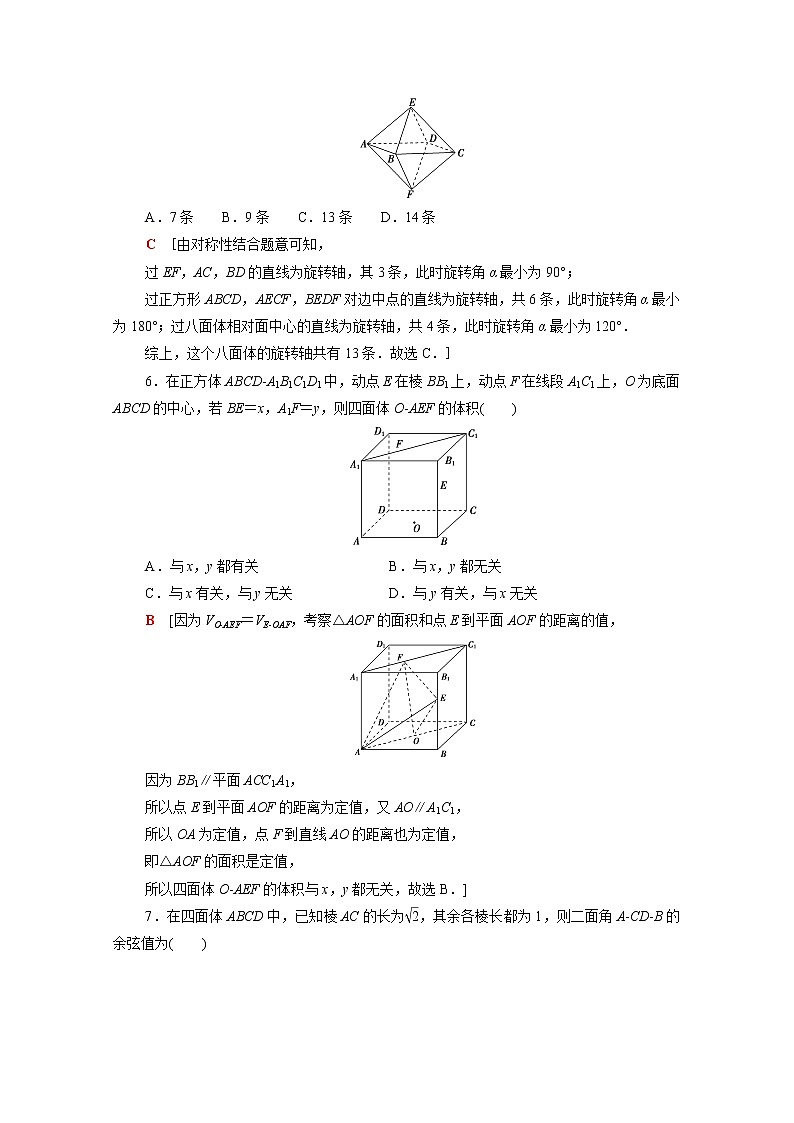
5．过空间几何体上的某两点的直线，如果把该几何体绕此直线旋转角α(0°＜α＜360°)，使该几何体与自身重合，那么称这条直线为该几何体的旋转轴．如图，八面体的每一个面都是正三角形，并且4个顶点A，B，C，D在同一平面内．则这个八面体的旋转轴共有(　　)

A．7条 B．9条 C．13条 D．14条
C　[由对称性结合题意可知，
过EF，AC，BD的直线为旋转轴，其3条，此时旋转角α最小为90°；
过正方形ABCD，AECF，BEDF对边中点的直线为旋转轴，共6条，此时旋转角α最小为180°；过八面体相对面中心的直线为旋转轴，共4条，此时旋转角α最小为120°．
综上，这个八面体的旋转轴共有13条．故选C．]
6．在正方体ABCD­A1B1C1D1中，动点E在棱BB1上，动点F在线段A1C1上，O为底面ABCD的中心，若BE＝x，A1F＝y，则四面体O­AEF的体积(　　)

A．与x，y都有关 B．与x，y都无关
C．与x有关，与y无关 D．与y有关，与x无关
B　[因为VO­AEF＝VE­OAF，考察△AOF的面积和点E到平面AOF的距离的值，

因为BB1∥平面ACC1A1，
所以点E到平面AOF的距离为定值，又AO∥A1C1，
所以OA为定值，点F到直线AO的距离也为定值，
即△AOF的面积是定值，
所以四面体O­AEF的体积与x，y都无关，故选B．]
7．在四面体ABCD中，已知棱AC的长为，其余各棱长都为1，则二面角A­CD­B的余弦值为(　　)

A． B．
C． D．
C　[取AC的中点E，CD的中点F，连接BE，EF，BF，则EF＝，BE＝，BF＝，因为EF2＋BE2＝BF2，所以△BEF为直角三角形，cos θ＝＝．]

8．在三棱锥P­ABC中，PA⊥平面ABC，AB⊥BC，若AB＝2，BC＝3，PA＝4，则该三棱锥的外接球的表面积为(　　)
A．13π B．20π C．25π D．29π
D　[如图，因为AB⊥BC，AB＝2，BC＝3，所以AC＝，△ABC外接圆的圆心为AC的中点O′．设外接球的球心为O，连接OO′，则OO′⊥平面ABC．因为PA⊥平面ABC，所以OO′∥PA，PA⊥AC，则点O在平面PAC内，且为△PAC的外接圆圆心，所以O为PC的中点，所以球的直径为PC，所以(2R)2＝AP2＋AC2，即R2＝，所以球的表面积为4πR2＝29π．]

二、选择题(本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分)
9．a，b为不重合直线，β为平面，下列结论正确的是(　　)
A．若a⊥β，b⊥β，则a∥b B．若a∥β，b∥β，则a∥b
C．若a∥β，b⊥β，则a⊥b D．若a∥β，b⊂β，则a∥b
AC　[若a⊥β，b⊥β，由直线与平面垂直的性质可得a∥b，故A正确；
若a∥β，b∥β，则a∥b或a与b相交或a与b异面，故B错误；
若b⊥β，则b垂直于β内的所有直线，b也垂直于平行于β的所有直线，又a∥β，可得a⊥b，故C正确；
若a∥β，b⊂β，则a∥b或a与b异面，故D错误．故选AC．]
10．如图所示，在正方体ABCD­A1B1C1D1中，M，N分别为棱C1D1，C1C的中点，其中正确的是(　　)

A．直线AM与C1C是相交直线
B．直线AM与BN是平行直线
C．直线BN与MB1是异面直线
D．直线MN与AC所成的角为60°
CD　[结合题图，显然直线AM与C1C是异面直线，直线AM与BN是异面直线，直线BN与MB1是异面直线．连接D1C，AD1(图略)，直线MN与AC所成的角即直线D1C与AC所成的角，在等边三角形AD1C中，易知∠ACD1＝60°，所以直线MN与AC所成的角为60°，故选CD．]
11．如图，在正四棱锥S­ABCD中，E，M，N分别是BC，CD，SC的中点．当点P在线段MN上运动时，下列四个结论中恒成立的是(　　)

A．EP⊥AC
B．EP∥BD
C．EP∥平面SBD
D．EP⊥平面SAC
AC　[如图所示，连接NE，ME．∵E，M，N分别是BC，CD，SC的中点，∴EN∥SB，MN∥SD，又EN∩MN＝N，SB∩SD＝S，

∴平面SBD∥平面NEM，∴EP∥平面SBD，选项C恒成立．由正四棱锥S­ABCD，知AC⊥平面SBD，∴AC⊥平面NEM，∴AC⊥EP，选项A恒成立．选项B，D对于线段MN上的任意一点P不一定成立，故选AC．]
12．如图，在四棱锥P­ABCD中，底面ABCD为菱形，∠DAB＝60°，侧面PAD为正三角形，且平面PAD⊥平面ABCD，则下列说法正确的是(　　)

A．在棱AD上存在点M，使AD⊥平面PMB
B．异面直线AD与PB所成的角为90°
C．二面角P­BC­A的大小为45°
D．BD⊥平面PAC
ABC　[如图，对于A，取AD的中点M，连接PM，BM，

∵侧面PAD为正三角形，
∴PM⊥AD，又底面ABCD是菱形，∠DAB＝60°，
∴△ABD是等边三角形，
∴AD⊥BM，又PM∩BM＝M，PM，BM⊂平面PMB，∴AD⊥平面PBM，故A正确．
对于B，∵AD⊥平面PBM，∴AD⊥PB，即异面直线AD与PB所成的角为90°，故B正确．
对于C，∵平面PBC∩平面ABCD＝BC，BC∥AD，
∴BC⊥平面PBM，∴BC⊥PB，BC⊥BM，
∴∠PBM是二面角P­BC­A的平面角，设AB＝1，则BM＝，PM＝，
在Rt△PBM中，tan∠PBM＝＝1，即∠PBM＝45°，故二面角P­BC­A的大小为45°，故C正确．
对于D，因为BD与PA不垂直，所以BD与平面PAC不垂直，故D错误．故选ABC．]
三、填空题(本大题共4小题，每小题5分，共20分，把答案填在题中的横线上)
13．已知一圆锥的侧面展开图是半径为2的半圆，则该圆锥的表面积为________，体积为________．(本题第一空2分，第二空3分)
3π　π　[设圆锥的底面半径为r，根据题意，得2πr＝2π，解得r＝1，根据勾股定理，得圆锥的高为＝，所以圆锥的表面积S＝×π×22＋π×12＝3π，体积V＝×π×12×＝π．]
14．已知正四棱锥的侧棱长为2，侧棱与底面所成的角为60°，则该四棱锥的高为________．
3　[如图，过点S作SO⊥平面ABCD，连接OC，则∠SCO＝60°，

∴SO＝sin 60°·SC＝×2＝3．]
15．如图， 在三棱柱A1B1C1­ABC中，D，E，F分别是AB，AC，AA1的中点，设三棱锥F­ADE的体积为V1，三棱柱A1B1C1­ABC的体积为V2，则V1∶V2＝________．

1∶24　[因为D，E分别是AB，AC的中点，
所以S△ADE∶S△ABC＝1∶4． 又F是AA1的中点，
所以A1到底面的距离H为F到底面距离h的2倍，即三棱柱A1B1C1­ABC的高是三棱锥F­ADE高的2倍， 所以V1∶V2＝＝＝1∶24．]
16．长方体ABCD­A1B1C1D1中，E为棱CC1上任意一点，F为底面A1B1C1D1(除C1外)上一点，已知F在底面ABCD上的射影为H，若再增加一个条件，就能得到CH⊥AD，现给出以下条件：
①EF⊥B1C1；
②F在B1D1上；
③EF⊥平面AB1C1D；
④直线FH和FE在平面AB1C1D内的射影为同一条直线．
其中一定能成为增加的条件的是________．(填序号)
①③④　[对于①，因为AD∥B1C1，EF⊥B1C1，所以AD⊥EF，又AD⊥FH，FH∩EF＝F，所以AD⊥平面FHCE，所以AD⊥CH；
对于②，F在B1D1上，当点F与点B1重合时，CH就是CB，显然CB不垂直AD；
对于③，因为EF⊥平面AB1C1D，所以EF⊥AD，由①可得AD⊥CH；
对于④，因为直线FH和FE在平面AB1C1D内的射影为同一条直线，即平面FHCE⊥平面AB1C1D，又平面FHCE⊥平面ABCD，且平面ABCD∩平面AB1C1D＝AD，所以AD⊥平面FHCE，所以AD⊥CH．]
四、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤)
17．(本小题满分10分)把一个圆锥截成圆台，已知圆台的上、下底面半径的比是1∶4，母线长为10 cm，求圆锥的母线长 ．
[解]　如图，设圆锥的母线长为l，圆台上、下底面的半径分别为r、R．

因为＝，所以＝，
所以l＝ cm．
即圆锥的母线长为 cm．
18．(本小题满分12分)如图，三棱柱ABC­A1B1C1的侧棱与底面垂直，AC＝9，BC＝12，AB＝15，AA1＝12，点D是AB的中点．

(1)求证：AC⊥B1C；
(2)求证：AC1∥平面CDB1．
[证明]　(1)∵C1C⊥平面ABC，
∴C1C⊥AC．
∵AC＝9，BC＝12，AB＝15，∴AC2＋BC2＝AB2，
∴AC⊥BC．
又BC∩C1C＝C，∴AC⊥平面BCC1B1，
而B1C⊂平面BCC1B1，
∴AC⊥B1C．
(2)连接BC1交B1C于点O，连接OD．如图，

∵O，D分别为BC1，AB的中点，
∴OD∥AC1．又OD⊂平面CDB1，
AC1⊄平面CDB1．
∴AC1∥平面CDB1．
19．(本小题满分12分)如图，已知三棱锥P­ABC，PA⊥平面ABC，∠ACB＝90°，∠BAC＝60°，PA＝AC，M为PB的中点．

(1)求证：PC⊥BC；
(2)求二面角M­AC­B的大小．
[解]　(1)证明：由PA⊥平面ABC，
所以PA⊥BC，
又因为∠ACB＝90°，
即BC⊥AC，PA∩AC＝A，
所以BC⊥平面PAC，
所以PC⊥BC．
(2)取AB中点O，连接MO，过O作HO⊥AC于H，
连接MH，

因为M是BP的中点，所以MO∥PA，
又因为PA⊥平面ABC，所以MO⊥平面ABC，
所以∠MHO为二面角M­AC­B的平面角，设AC＝2，则BC＝2，MO＝1，OH＝，
在Rt△MHO中，tan∠MHO＝＝，
所以二面角M­AC­B的大小为30°．
20．(本小题满分12分)如图，在四棱锥P­ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD＝1，BC＝3，CD＝4，PD＝2．

(1)求异面直线AP与BC所成角的余弦值；
(2)求证：PD⊥平面PBC；
(3)求直线AB与平面PBC所成角的正弦值．
[解]　(1)如图，由已知AD∥BC，故∠DAP或其补角为异面直线AP与BC所成的角．因为AD⊥平面PDC，所以AD⊥PD．在Rt△PDA中，由已知，得AP＝＝，所以cos∠DAP＝＝．

所以异面直线AP与BC所成角的余弦值为．
(2)因为AD⊥平面PDC，直线PD⊂平面PDC，所以AD⊥PD．
又BC∥AD，所以PD⊥BC，又PD⊥PB，
PB∩BC＝B，所以PD⊥平面PBC．
(3)过点D作AB的平行线交BC于点F，连接PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角．
因为PD⊥平面PBC，故PF为DF在平面PBC上的射影，所以∠DFP为直线DF与平面PBC所成的角．
由于AD∥BC，DF∥AB，故BF＝AD＝1，由已知，得CF＝BC－BF＝2．
又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得DF＝＝2，在Rt△DPF中，可得sin∠DFP＝＝．
所以直线AB与平面PBC所成角的正弦值为．
21．(本小题满分12分)如图，几何体ABC­A1DC1由一个正棱柱截去一个三棱锥而得，AB＝4，AA1＝3，A1D＝1，AA1⊥平面ABC，M为AB的中点，E为棱AA1上一点，且EM∥平面BC1D．

(1)若点N在棱BC上，且BN＝2NC，证明：EN∥平面BC1D；
(2)过A作平面BCE的垂线，垂足为O，确定O的位置(说明作法及理由)，并求线段OE的长．
[解]　(1)证明：∵EM∥平面BC1D，EM⊂平面ABDA1，平面ABDA1∩平面BC1D＝BD，

∴BD∥EM．
过D作DH⊥AB于H，连接CH，则CH∥C1D，
则HM＝AB－AB＝AB，
∴HM∶MB＝CN∶NB＝1∶2，
∴MN∥CH，则MN∥C1D．
∵EM∩MN＝M，∴平面EMN∥平面BC1D．
∵EN⊂平面EMN，∴EN∥平面BC1D．
(2)在线段AB上取一点F，使BF＝A1D＝1，则A1F∥BD，由(1)知EM∥BD，
∴EM∥A1F，∴＝＝，
∴AE＝×3＝2．
取BC的中点G，连接AG，EG，过A作AO⊥EG于O，则AO⊥平面BCE．
证明如下：
由题意可知，△ABC为等边三角形，则AG⊥BC，又AA1⊥平面ABC，∴AA1⊥BC．
∵AG∩AA1＝A，∴BC⊥平面AEG，∴BC⊥AO．
又EG∩BC＝G，∴AO⊥平面BCE．
由射影定理可得，AE2＝OE·EG，又AE＝2，EG＝2，∴OE＝．
22．(本小题满分12分)已知正三角形A′BC的边长为a，CD是A′B边上的高，E，F分别是A′C，BC的中点，现将三角形A′DC沿CD翻折至△ADC的位置，使平面ADC⊥平面BCD，如图所示．

(1)试判断翻折后直线AB与平面DEF的位置关系，并说明理由；
(2)若三棱锥E­DFC的体积为，求实数a的值；
(3)在线段AC上是否存在一点P，使得BP⊥DF？若存在，求出的值；若不存在，请说明理由．
[解]　(1)AB∥平面DEF．理由如下：
在△ABC中，∵E，F分别是AC，BC的中点，∴EF∥AB，
又AB⊄平面DEF，EF⊂平面DEF，∴AB∥平面DEF．
(2)由题意，得AD⊥CD．

∵平面ADC⊥平面BCD，∴AD⊥平面BCD．
取CD的中点M，连接EM，则EM∥AD，
∴EM⊥平面BCD，且EM＝．
易得S△DFC＝××＝．
∵三棱锥E­DFC的体积为，
∴××＝，解得a＝2．
(3)在线段AC上存在一点P，使得BP⊥DF．理由如下：
易知三角形BDF为正三角形，过B作BK⊥DF交DC于点K，连接KF，过K作KP∥DA交AC于点P，连接BP，则点P即所求．
∵AD⊥平面BCD，KP∥AD，
∴PK⊥平面BCD，∴PK⊥DF．
又BK⊥DF，PK∩BK＝K，
∴DF⊥平面PKB，∴DF⊥PB．
又∠DBK＝∠KBC＝∠BCK＝30°，
∴DK＝KF＝KC．
故＝＝，从而＝．