






初中北师大版第五章 一元一次方程5.6 应用一元一次方程——追赶小明课前预习ppt课件
展开行程问题中基本的量有哪些?
行程三要素:路程=速度×时间
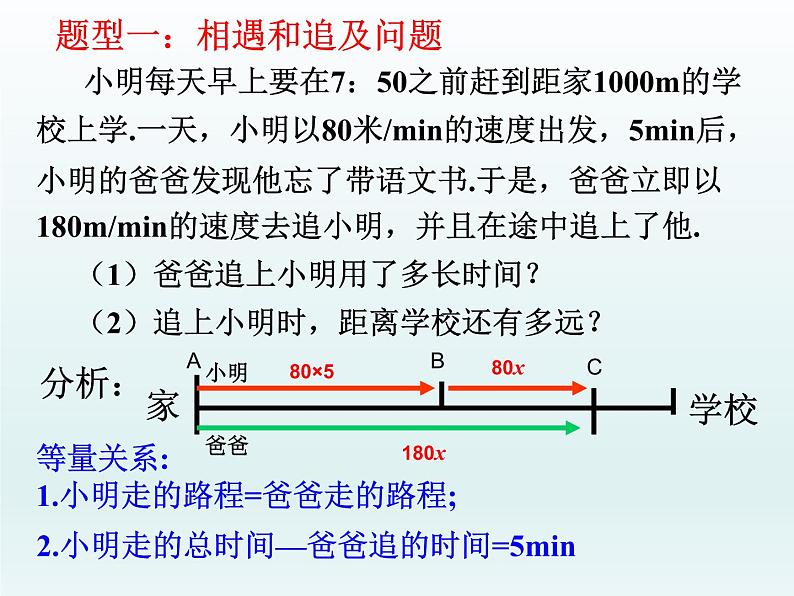
题型一:相遇和追及问题 合作探究: 小明每天早上要在7:50之前赶到距家1000m的学校上学.一天,小明以80m/min的速度出发,5min后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180m/min的速度去追小明,并且在途中追上了他.(1)爸爸追上小明用了多长时间?(2)追上小明时,距离学校还有多远?
等量关系:1.小明走的路程=爸爸走的路程;
2.小明走的总时间—爸爸追的时间=5min
小明每天早上要在7:50之前赶到距家1000m的学校上学.一天,小明以80米/min的速度出发,5min后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180m/min的速度去追小明,并且在途中追上了他.(1)爸爸追上小明用了多长时间?(2)追上小明时,距离学校还有多远?
题型一:相遇和追及问题
解:(1)设爸爸追上小明用了x分钟, 据题意得 80×5+80x=180x. 解,得 x=4. 答:爸爸追上小明用了4分钟. (2)180×4=720(米), 1000-720=280(米). 答:追上小明时,距离学校还有280米.
对于同向同地不同时的问题,如图所示,甲的时间+时间差=乙的时间甲的行程=乙先走的路程+乙后走的路程.
注意:同向而行注意始发时间和地点.
对于行程问题,通常借助“线段图”来分析问题中的数量关系.
甲、乙两人同向出发,甲追乙这类问题为追及问题:
上题中,若小明晚上住在距自己家400m的爷爷家(假设小明从家到学校必经爷爷家)第二天准备出发去学校时发现忘带数学书,打电话通知爸爸送来.爸爸立即以180m/min的速度从家出发,同时小明以80m/min的速度从爷爷家去学校,并且在途中爸爸追上了他,问爸爸追上小明用了多长时间?
对于同向同时不同地的问题,如图所示,甲的时间=乙的时间乙的路程+路程差=甲的路程;
上题中,若当小明到校后发现忘带英语书,打电话通知爸爸送来.爸爸立即以180m/min的速度从家出发,同时小明以100m/min的速度从学校返回,两人几分钟后相遇?
两人从两地出发相向而行的行程问题称为相遇问题.
往往根据路程之和等于总路程列方程.如图所示,甲的行程+乙的行程=两地距离.
育红学校七年级学生步行到郊外旅行.七(1)班的学生组成前队,步行速度为4km/h,七(2)班的学生组成后队,速度为6km/h.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h. 根据上面的事实提出问题并尝试去解答.
问题3:联络员在前队出发多少时间后第一次追上前队?
问题1:后队追上前队用了多长时间 ?
问题2:后队追上前队时联络员行了多少路程?
育红学校七年级学生步行到郊外旅行,1班的学生 组成前队,步行的速度为4km/h,2班的学生组成 后队,速度为6km/h,前队出发1h后,后队出 发,同时后队派一名联络员骑自行车在两队之间不间断 地 来回进行联络,他骑车的速度为12km/h.
解:设后队追上前队用了xh,由题意得:
6x = 4x + 4
答:后队追上前队时用了2h.
解:由问题1得后队追上前队用了2小时,因此 联络员共行进了
12 × 2 = 24 (千米)答:后队追上前队时联络员行了24千米.
育红学校七年级学生步行到郊外旅行.(1)班的学生组成前队,步行速度为4km/h,(2)班的学生组成后队,速度为6km/h.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.
问题3:联络员在前队出发多长时间后第一次追上前队?
解:设联络员在前队出发yh后第一次追上前队, 由题意列方程得;
答:联络员在前队出发后1.5 小时后第一次追上前队.
4y = 12(y-1)
解方程得: y = 1.5
育红学校七年级学生步行到郊外旅行.(1)班的学生组成前队,步行速度为4km/h,(2)班的学生组成后队,速度为6km/h.前队出发1h后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.
解:设快车x小时追上慢车,据题意得: 85x=450+65x. 解,得 x=22.5. 答:快车22.5小时追上慢车.
练习2:甲、乙两站间的路程为450千米,一列慢车从甲站 开出,每小时行驶65千米,一列快车从乙站开出, 每小时行驶85千米.设两车同时开出,同向而行, 则快车几小时后追上慢车?
分析:等量关系:快车所用时间=慢车所用时间; 快车行驶路程=慢车行驶路程+相距路程.
练习2变式:甲、乙两站间的路程为450千米,一列慢车从甲站 开出,每小时行驶65千米,一列快车从乙站开出, 每小时行驶85千米.设两车同时开出,相向而行, 则快车几小时后与慢车相遇?
解:设快车x小时追上慢车,据题意得: 85x+65x=450. 解,得 x=3. 答:快车3小时追上慢车.
能力拔高:A、B两地相距216km,甲、乙分别在A、B两地,若甲骑车的速度为15km/h,乙骑车的速度为12km/h.(1)甲、乙同时出发,背向而行,则几小时后他们相距351千米?(2)甲、乙相向而行,甲出发三小时后乙才出发,则乙出发几小时后两人相遇?(3)甲、乙相向而行,要使他们相遇于AB的中点,乙要比甲先出发几小时?
(1)对于同向同时不同地的问题,如图所示,甲的时间=乙的时间乙的路程+路程差=甲的路程;
(2)对于同向同地不同时的问题,如图所示,甲的时间+时间差=乙的时间.甲的行程=乙先走的路程+乙后走的路程.
初中北师大版5.6 应用一元一次方程——追赶小明授课课件ppt: 这是一份初中北师大版<a href="/sx/tb_c9943_t3/?tag_id=26" target="_blank">5.6 应用一元一次方程——追赶小明授课课件ppt</a>,共15页。PPT课件主要包含了学习新知,巩固练习,检测反馈等内容,欢迎下载使用。
初中数学北师大版七年级上册5.6 应用一元一次方程——追赶小明课堂教学ppt课件: 这是一份初中数学北师大版七年级上册5.6 应用一元一次方程——追赶小明课堂教学ppt课件,共18页。PPT课件主要包含了导入新课,探究新知,等量关系,解得x4,根据题意得,应用举例,千米时,同时出发,kmh,课堂小结等内容,欢迎下载使用。
2021学年5.6 应用一元一次方程——追赶小明教学ppt课件: 这是一份2021学年5.6 应用一元一次方程——追赶小明教学ppt课件,共26页。PPT课件主要包含了龟兔赛跑,行程问题,请用线段图表示,小明所跑的路程,小彬所跑的路程,小强所跑的路程,追及问题同向同时,甲在前乙在后,相遇问题相向而行,归纳小结等内容,欢迎下载使用。













