初中数学1 认识一元二次方程课堂教学ppt课件

这是一份初中数学1 认识一元二次方程课堂教学ppt课件，共25页。PPT课件主要包含了你能行吗，≠±1，＝－1，估算一元二次方程的解，回味无穷等内容，欢迎下载使用。

幼儿园某教室矩形地面的长为8m，宽为5m，现准备在地面正中间铺设一块面积为１８m2 的地毯 ，四周未铺地毯的条形区域的宽度都相同，你能求出这个宽度吗？
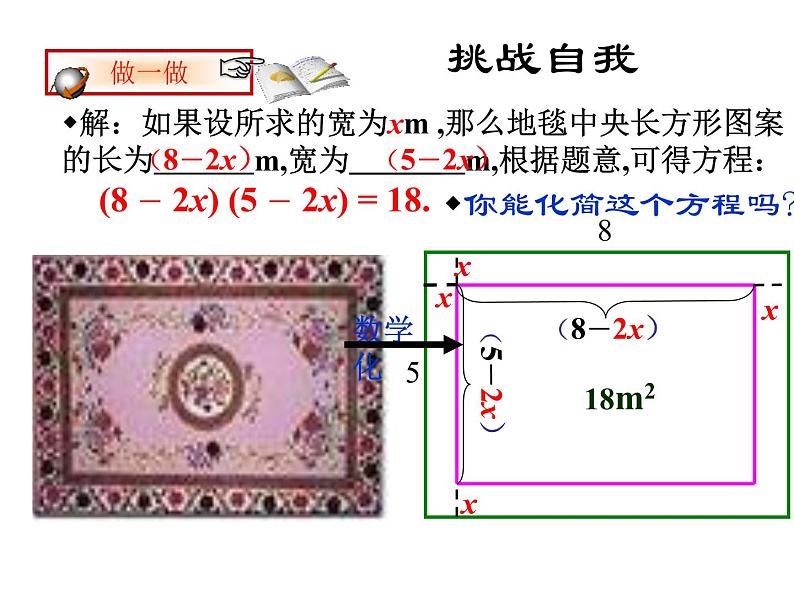
解：如果设所求的宽为xm ,那么地毯中央长方形图案的长为 m,宽为　　　 m,根据题意,可得方程：
(8 － 2x) (5 － 2x) = 18.
观察下面等式：１０２＋１１２＋１２２＝１３２＋１４２你还能找到其他的五个连续整数，使前三个数的平方和等于后两个数的平方和吗？
如果设五个连续整数中的第一个数为x，那么后面四个数依次可表示为：　　　　，　　　　，　　　　，　　　　．
根据题意，可得方程：　　　　　　　　　　　　 .
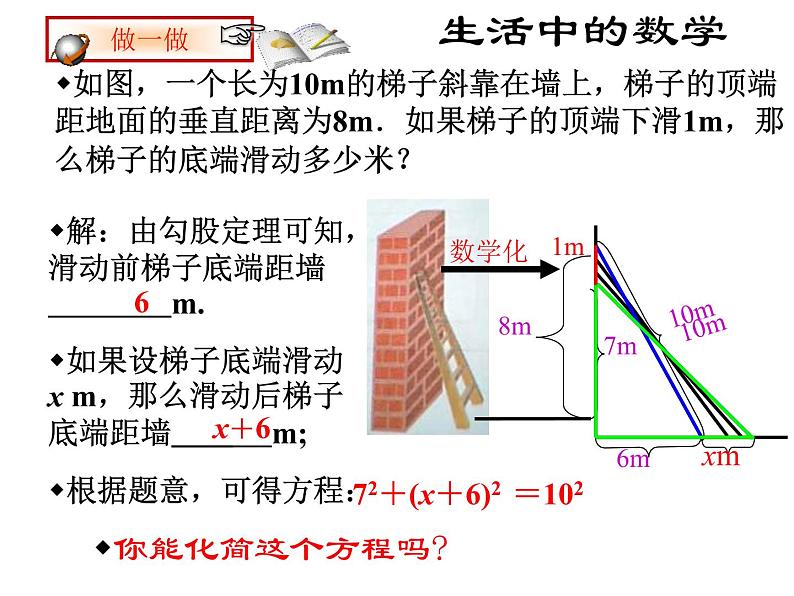
如图，一个长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8m．如果梯子的顶端下滑1m，那么梯子的底端滑动多少米？
解：由勾股定理可知，滑动前梯子底端距墙　　　　m.如果设梯子底端滑动x m，那么滑动后梯子底端距墙　　 m;根据题意，可得方程：
72＋(x＋6)2 ＝102
上面的方程都是只含有　　　　　　的　　　　 ，并且都可以化为　　　　　　　　　　　　　　　　　 的形式，这样的方程叫做一元二次方程．
由上面三个问题，我们可以得到三个方程：
把ax２＋bx＋c＝０(a，b，c为常数,a≠０)称为一元二次方程的一般形式，其中ax２ ， bx ， c分别称为二次项、一次项和常数项，a， b分别称为二次项系数和一次项系数．
(8-2x)(５-２x)=18;
即 2x2 － 13x ＋ 11 = 0 .
x２+（x+1)２+(x+2)２=(x+3)２+(x+４)２
即 x2 － 8x － 20＝0.
（ x＋６）２＋７２＝１０２
即 x2 ＋12 x －15 ＝0.
上述三个方程有什么共同特点？
ax２＋bx＋c＝０(a，b，c为常数, a≠０)
下列方程哪些是一元二次方程?
(2)2x2－5xy＋6y＝0
(5)x2＋2x－3＝1＋x2
(1)7x2－6x＝0
解: (1)、 (4)
1.关于x的方程(k－3)x2 ＋ 2x－1＝0,当k _______ 　　　时，是一元二次方程．
2.关于x的方程(k2－1)x2 ＋ 2 (k－1) x ＋ 2k ＋ 2＝0,当k 　　　时，是一元二次方程．当k 　　　时，是一元一次方程．
解：设竹竿的长为x尺,则门的宽 度为 尺,长为 尺,依题意得方程：
１．从前有一天，一个醉汉拿着竹竿进屋，横拿竖拿都进不去，横着比门框宽４尺，竖着比门框高２尺，另一个醉汉教他沿着门的两个对角斜着拿竿，这个醉汉一试，不多不少刚好进去了．你知道竹竿有多长吗？请根据这一问题列出方程．
(x－4)2＋ (x－2)2＝ x2
x2－12 x ＋20 ＝ 0
２.把方程(3x＋2)2＝4(x－3)2化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项．
解：将原方程化简为： 9x2＋12x＋4＝4(x2－6x＋9)
5x2 ＋ 36 x － 32＝0
一次项系数为 ，
常数项为 .
4 x2 －24x ＋36
１．根据题意，列出方程：
（１）有一面积为54m2的长方形，将它的一边剪短5m，另一边剪短2m，恰好变成一个正方形，这个正方形的边长是多少？
解：设正方形的边长为xm，则原长方形的长为(x＋5) m,宽为(x＋2) m，依题意得方程：
(x＋5) (x＋2) ＝54
x2 ＋ 7x－44 ＝0
（２）三个连续整数两两相乘，再求和，结果为242，这三个数分别是多少？
x (x＋1) ＋ x(x＋2) ＋ (x＋1) (x＋2) ＝242.
x2 ＋2x－8 0＝0.
解：设第一个数为x，则另两个数分别为x＋１, x＋2，依题意得方程：
2.把下列方程化为一元二次方程的形式，并写出它的二次项系数、一次项系数和常数项：
或－7x2 ＋0 x＋4＝0
或7x2 － 4＝0
解：设教室未铺地毯区域的宽为xm , 根据题意得
你能求出x吗?怎么去估计x呢？
即2x2-13x+11 = 0.
x可能小于0吗?说说你的理由.
x可能大于4吗?可能大于2.5吗?说说你的理由.
因此,x取值的大致范围是:0在0完成下表(取值计算,逐步逼近):
由此看出,可以使(8 － 2x) (5 － 2x)的值为18的x=1.故可知所求的宽为1m.
你还有其它求解方法吗?与同伴交流.
如果将(8-2x)(5-2x)=18看作是6×3=18.则有8-2x=6, 5-2x=3.从而也可以解得x=1.
怎么样,你还敢挑战吗?你能总结出估算的方法步骤和提高估算的能力吗?
0.5 1 1.5 2
28 18 10 4…
解：如果设梯子底端滑动x m，根据题意得
你能猜得出x取值的大致范围吗?
72+(x+6)2=102
即 x2+12x-15=0
0.5 1 1.5 2
-8.75 -2 5.25 13
可知x取值的大致范围是:1在1由此看出,可以使x2+12x-15的值接近0的x为整数的值是x=1;精确到十分位的x的值约是1.2.
你能算出精确到百分位的值吗?
1.1 1.2 1.3 1.4
-0.59 0.84 2.29 3.76
即 x2-8x-20=0.
你能求出这五个整数分别是多少吗?
１.学习了什么是一元二次方程，以及它的一般形式ax２＋bx＋c＝０（a，b，c为常数，a≠０）和有关概念，如二次项、一次项、常数项、二次项系数、一次项系数．２.会用一元二次方程表示实际生活中的数量关系3.学习了估算一元二次方程ax２＋bx＋c＝０（a，b，c为常数，a≠０）4.近似解的方法；知道了估算步骤:先确定大致范围;再取值计算,逐步逼近.
本节课你又学会了哪些新知识呢？学习了估算一元二次方程ax２＋bx＋c＝０（a，b，c为常数，a≠０）近似解的方法；知道了估算步骤:先确定大致范围;再取值计算,逐步逼近.想一想,有没有便捷的方法去求方程中的未知数呢?
根据题意,列出方程,并估算方程的解：
1.一面积为120m2的矩形苗圃，它的长比宽多2m，苗圃的长和宽各是多少？
解：设苗圃的宽为xm，则长为(x＋2) m, 根据题意得：
x (x＋2) ＝120.
x2 ＋ 2x－120 ＝0.
根据题意,x的取值范围大致是0完成下表(在0由此看出,可以使x2+2x-120的值为0的x=10.故可知宽为10m,长为12m.
8 9 10 11
-40 -21 0 23
2.一名跳水运动员进行10m跳台跳水训练,在正常情况下,运动员必需在距水面5m以前完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误.假设运动员起跳后的运动时间t(s)和运动员距水面的高度h(m)满足关系: h＝10+2.5t-5t2.那么他最多有多长时间完成规定动作？
5＝10+2.5t-5t2.
2t2 –t－2＝0.
完成下表(在0由此看出,可以使2t2-t-2的值为0的t的范围是1.2-2 -1 4 13
根据题意,t的取值范围大致是0 0 1 1.1 1.2 1.3 1.4 2 3
0 1 2 3
-2 -1 -0.68 -0.32 0.08 0.52 4 13