2020年上海市嘉定区中考一模数学试卷（期末）

这是一份2020年上海市嘉定区中考一模数学试卷（期末），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共6小题；共30分）
1. 下列选项中的两个图形一定相似的是
A. 两个等腰三角形B. 两个矩形
C. 两个菱形D. 两个正五边形

2. 在 Rt△ABC 中，∠C=90∘，AB=10，AC=8．下列四个选项，不正确是
A. sinA=45B. csA=45C. tanA=34D. ctA=43

3. 如果 A−2,n，B2,n，C4,n+12 这三个点都在同一个函数的图象上，那么这个函数的解析式可能是
A. y=2xB. y=−2xC. y=−x2D. y=x2

4. 如图，在平行四边形 ABCD 中，设 AB=a，AD=b，那么向量 OC 可以表示为
A. 12a+12bB. 12a−12bC. −12a+12bD. −12a−12b

5. 三角形的重心是
A. 三角形三条边上中线的交点B. 三角形三条边上高线的交点
C. 三角形三条边垂直平分线的交点D. 三角形三条内角平分线的交点

6. 下列四个选项中的表述，一定正确的是
A. 经过半径上一点且垂直于这条半径的直线是圆的切线
B. 经过半径的端点且垂直于这条半径的直线是圆的切线
C. 经过半径的外端且垂直于这条半径的直线是圆的切线
D. 经过一条弦的外端且垂直于这条弦的直线是圆的切线

二、填空题（共12小题；共60分）
7. 如果 2a=3b，那么 ab= ．

8. 如果将一个三角形保持形状不变但周长扩大为原三角形周长的 9 倍，那么扩大后的三角形面积为原三角形面积的 倍．

9. 在某一时刻测得一根高为 1.8 m 的竹竿的影长为 0.9 m，如果同时同地测得一栋的影长为 27 m，那么这栋楼的高度为 m．

10. 在 △ABC 中，D，E 分别是边 AB，AC 上的点，如果 AD=2，DB=1，AE=4，EC=2，那么 DEBC 的值为 ．

11. 抛物线 y=12x+12 的顶点坐标为 ．

12. 如果抛物线 y=−x2+bx 的对称轴为 y 轴，那么实数 b 的值等于 ．

13. 将抛物线 y=x2+4x+5 向右平移两个单位后，所得抛物线的表达式为 ．

14. 已知抛物线 y=x2−2x+c 经过点 A−1,y1 和 B1,y2，那么 y1 y2（从“>”或“0，
∴ 选择D：y=x2．
4. A【解析】由题意可得
OC=12AC=12AD+AB=12a+b=12a+12b.
5. A
6. C【解析】由切线的判定定理可知：经过半径外端点且与这条半径垂直的直线是圆的切线，故A，B，D选项不正确，C选项正确，故选：C．
第二部分
7. 32
【解析】∵2a=3b，
∴ab=32．
8. 81
【解析】相似三角形面积比等于相似比的平方 S1S2=C1C22=81，
所以周长扩大 9 倍，面积扩大 81 倍．
9. 54
【解析】如图．
∵BEBC=DEAC，BE=0.9，DE=1.8，BC=27，
∴0.927=1.8AC，
∴AC=54．
10. 23
【解析】∵ADDB=AEEC=2，
∴DE∥BC，
∴ADAB=AEAC=DEBC=23．
11. −1,0
【解析】∵ 抛物线 y=12x+12，
∴ 顶点坐标为 −1,0．
12. 0
【解析】由题意可知，抛物线 y=−x2+bx 的对称轴为 y 轴，即直线 x=−b2a=−b2×−1=0，b=0．
13. y=x2+1
【解析】由题意可知，将抛物线向右平移两个单位后得：y=x−22+4x−2+5=x2+1．
14. >
【解析】由题意可知，抛物线 y=x2−2x+c 的开口向上（a>0），对称轴为直线 x=−b2a=−−22=1，
所以当 x≤1 时，y 随 x 的增大而减小，即 y1>y2．
15. 75
【解析】坡度 tanA=i=BCAC=30AC=1:2.5，解得 AC=75．
16. α=360n
【解析】因为正多边形边数为 n，则有 n⋅α=360∘，
则中心角 α=360n．
17. 32
【解析】如图，过点 A 作 AM⊥BC 于点 M，连接 OC．
∵AB=AC 且 BC=8，
∴BM=CM=12BC=4．
∵ 圆的半径等于 5，
∴OA=OC=5．
∴OM=OC2−MC2=3．
∴AM=8．
∴S△ABC=12×AM×BC=32．
18. 365
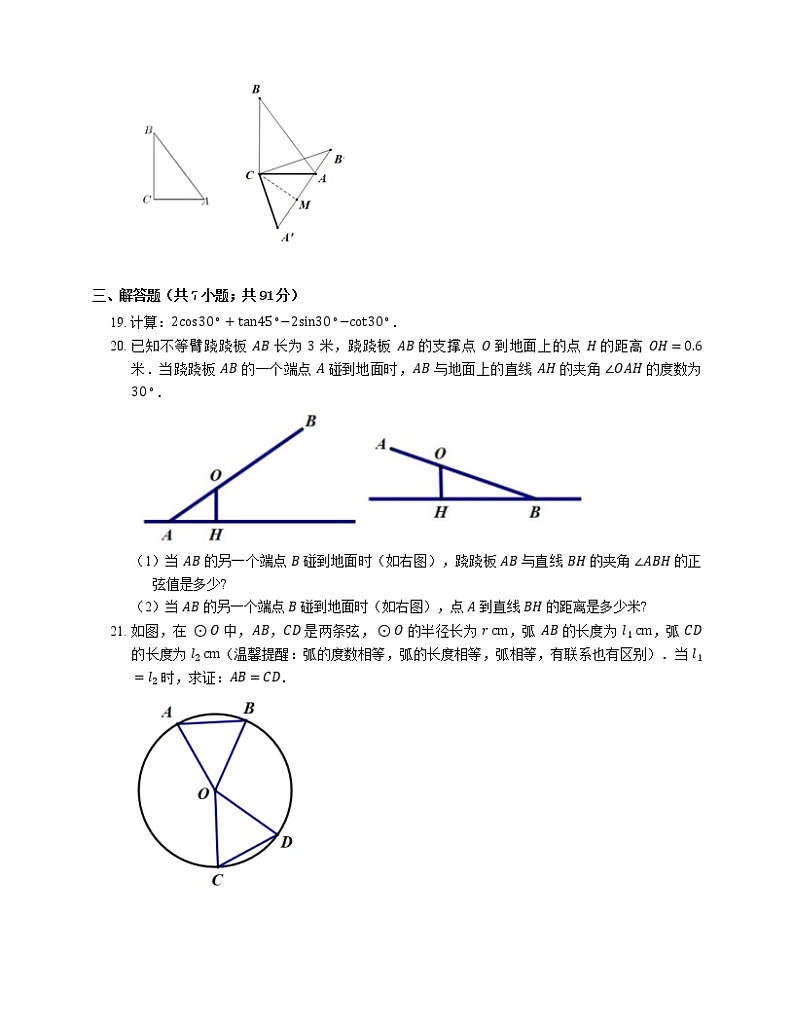
【解析】如图，△ABC 旋转得 △AʹBʹCʹ．
∵∠ACB=90∘，AB=10，csA=35，
∴AC=6．
∴BC=AB2−AC2=8．
由旋转可得 ∠Aʹ=∠A，AʹC=AC=6．
∴csAʹ=csA=35．
过点 C 作 CM⊥AAʹ 于点 M．
∴AʹM=185．
∴AAʹ=2AʹM=365．
第三部分
19. 2cs30∘+tan45∘−2sin30∘−ct30∘=2×32+1−2×12−3=3+1−1−3=0.
20. （1） ∵sin∠OAH=sin30∘=12，OH=0.6，
∴OA=12，
∵AB=3 m，AO=1.2 m，
∴OB=3−1.2=1.8 m，
在 Rt△BOH 中，sin∠ABH=OHOB=．
（2） 过 A 作 AC⊥BH，垂足为点 C．AC 长即为所求，
∴AC=ABsin∠ABH=3×13=1 m．
21. 令 ∠AOB=α，∠COD=β．
∵l1=l2，
∴απr1180=βπr2180．
∵AB 和 CD 在同圆中，r1=r2，
∴α=β．
∴AB=CD．
22. 过 A 作 AH 垂直于 BC 交 BC 的延长线于点 H．
由题意可得 ∠BAH=60∘，∠CAH=30∘，
∴∠ABH=30∘，∠ACH=60∘．
设 CH=x，在 Rt△ACH 中，tan60∘=AHCH=3，AH=3CH=3x．
在 Rt△ABH 中，tan30∘=AHBH=33，BH=3x．
∵BC=20，
∴BH=BC+CH=20+x．
∴20+x=3x，x=10．
AH=3x=103 海里 >10 海里．
∴ 不会有触礁危险．
23. （1） ∵DE∥BC，
∴∠DEB=∠EBC．
∵∠ABE=∠C，
∴△BED∼△CEB．
∴BEBC=DEBE．
∴BE2=DE⋅BC．
（2） ∵BE 平分 ∠ABC，
∴∠ABE=∠EBC．
∵DE∥BC，
∴∠DEB=∠EBC，∠C=∠AED=∠ABE．
∵∠ABE=∠DEB，
∴BD=DE．
∵∠A=∠A，∠AED=∠ABE，
∴△DAE∽△EAB
∴DEBE=AEAB．
24. （1） 如图．
将题图中的抛物线 y=x2 向下平移 2 个单位长，可得抛物线 y=x2−2．
画法：①列表；②描点（五点画图法）；③用光滑的曲线连接这五个点．
（2） 由题意，得点 Ax,y 的“关联点”为 A1x,y−x．
由点 Ax,y 在抛物线 y=x2 上，可得 Ax,x2，A1x,x2−x．
又 ∵A1x,y−x 在抛物线 y=x2−2 上，
∴x2−x=x2−2，解得 x=2．
将 x=2 代入 A1x,x2−x，得 A12,2．
（3） 点 Ax,y 的“待定关联点”为 A2x,x2−nx，
∵A2x,x2−nx 在抛物线 y=x2−n 的图象上，
∴x2−nx=x2−n．
∴n−nx=0，n1−x=0．
又 ∵n≠0，
∴x=1．
当 x=1 时，x2−nx=1−n，故可得 A21,1−n．
25. （1） ∵∠APB+∠PBA+∠PBA=180∘，∠APB+∠BAC=180∘，
∴∠BAC=∠PAB+∠PBA，
∴∠PBA=∠PAC，
∵∠APB=∠APC，
∴△PAB∽△PCA．
（2） ∵△PAB∽△PCA，
∴PAPC=PBPA=ABAC，
∴PCPB=PCPA⋅PAPB=ACAB2，
∵∠APB=120∘，
∴∠BAC=60∘，
∵∠ABC=90∘，
∴ACAB=2，
∴PCPB=4．
（3） ∵∠BAC=45∘，
∴∠APB=135∘=∠APC，
∴∠BPC=90∘，
tan∠BPC=PCPB=ACAB2，
∵∠BAC=45∘，△ABC 是等腰三角形，
当 BA=BC 时，由勾股定理可得 AC=2AB，tan∠BPC=22=2，
当 CA=CB 时，由勾股定理可得 AB=2BC，tan∠BPC=122=12，
当 AB=AC 时，tan∠BPC=1．
综上所述，tan∠PBC=2或12或1．