初中数学湘教版八年级上册3.1 平方根优秀课件ppt

这是一份初中数学湘教版八年级上册3.1 平方根优秀课件ppt，文件包含311平方根的意义及其性质-课件pptx、311平方根的意义及其性质-教学设计docx、311平方根的意义及其性质-试卷docx等3份课件配套教学资源，其中PPT共26页， 欢迎下载使用。
直接说出下列各式的结果.
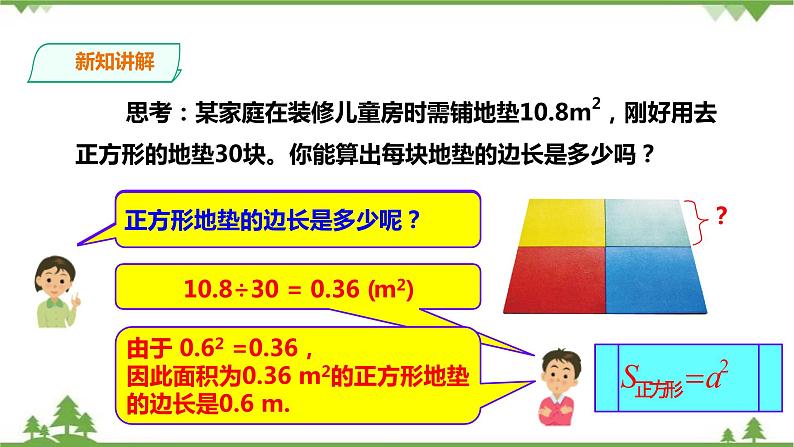
思考：某家庭在装修儿童房时需铺地垫10.8m2，刚好用去正方形的地垫30块。你能算出每块地垫的边长是多少吗？
每块正方形地垫的面积是多少呢？
10.8÷30 = 0.36 (m2)
正方形地垫的边长是多少呢？
由于 0.62 =0.36，因此面积为0.36 m2的正方形地垫的边长是0.6 m.
　　 如果有一个数r，使得r2=a，那么我们把r叫做a的一个平方根,也叫做二次方根.
若r2=a，则r是a的一个平方根
例如，由于22 = 4, 因此2是4的一个平方根.
因为（-3）2 = 9, 因此_______是9的一个平方根.
想一想：4的平方根除了2以外，还有其他的数吗?
其实，我也是你的平方根
因为（-2)2=4，因此-2 也是4的一个平方根.
4的平方根有且只有两个：2与-2.
练习1：分别说出9，16，25，49 的平方根是多少？
解：9的平方根是±3 ，16的平方根是±4 ，25的平方根是±5 ，49的平方根是±7.
想一想：一个正数有几个平方根？它们之间有什么关系呢？
即：如果r 是正数a的一个平方根，那么a的平方根有且只有两个：r与-r.
我们把正数a的正平方根叫作a的算术平方根
这样，正数a平方根可以用 表示
例如，4的平方根是2与-2，即
说一说：零的平方根是多少？负数有平方根吗?
由于02 = 0,而非零数的平方不等于0,因此零的平方根就是0本身. 我们把0的平方根也叫做0的算术平方根.
在迄今为止我们所认识的数中， 任何一个数的平方都不会是负数，因此负数没有平方根.
（1）正数有两个平方根,它们互为相反数;（2） 0的平方根是0；（3）负数没有平方根.
平方根与算术平方根的联系与区别：
联系： 1.包含关系：平方根包含算术平方根，算术平方根是平方根中的一个.
2.只有非负数才有平方根和算术平方根.
1.个数不同：一个正数有两个平方根，但只有一个算术平方根.
2.表示法不同：平方根表示为 ，而算术平方根表示为
思 考：对于任意数a， 一定等于a 吗?
想一想： 的结果是多少呢？
想一想：你发现了什么呢？
讨论： 与 有区别吗？
平方在外面，直接去根号和平方.
平方在里面，要加绝对值，分类来讨论.
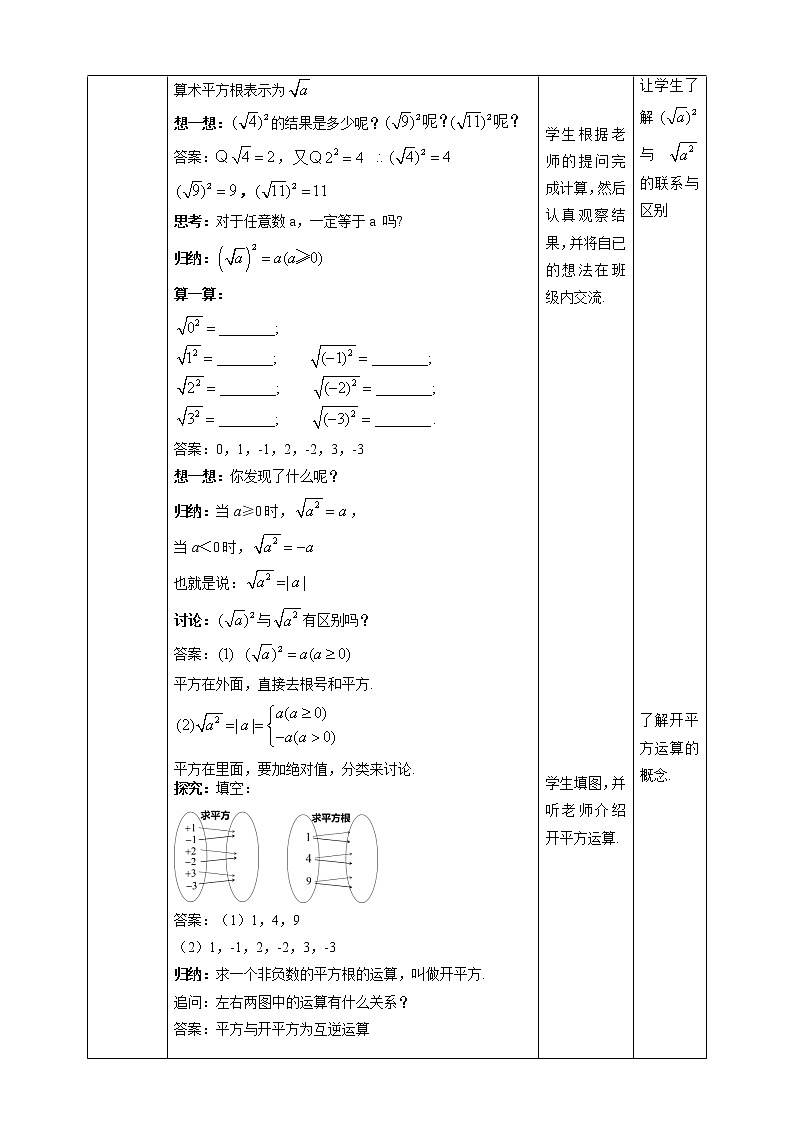
左右两图中的运算有什么关系？
求一个非负数的平方根的运算，叫做开平方.
例1：分别求下列各数的平方根：36； ； 1.21.
解：（1）∵62＝36，∴36的平方根是6与-6，即 （2）∵ ，∴ 的平方根是 与即 （3）∵1.12＝1.21， ∴1.21的平方根是1.1与-1.1，即
练习2. 分别求 64， ， 6.25 的平方根.
解：（1）∵82＝64，∴64的平方根是8与-8，即 （2）∵ ，∴ 的平方根是 与即 （3）∵2.52＝6.25， ∴6.25的平方根是2.5与-2.5，即
例2：分别求下列各数的算术平方根：100； ；0.49.
解：（1）∵102＝100，∴ （2）∵ ，∴ （3）∵0.72＝0.49， ∴
正数的算术平方根中有一个
算术平方根就是正平方根.
练习3. 分别求 81， ， 0.16 的算术平方根.
解：（1）∵92＝81，∴ （2）∵ ，∴ （3）∵0.42＝0.16， ∴
1．下列说法正确的是( )A．负数没有平方根B．任何一个数的平方根都比它本身大C．只有正数才有平方根D．一个数的平方根不可能与它本身相等
2. 9的算术平方根是（ ）. A.-3 B.3 C. ±3 D.81
3. 判断下列说法是否正确.
（4）(-4)2的平方根是-4.
（1） 是 的一个平方根；
（2） 是6的算术平方根；
（3） 的值是±4；
1、什么是平方根？算术平方根？
2、说一说平方根的性质.
如果有一个数r，使得r2=a，那么我们把r叫做a的一个平方根,也叫做二次方根.我们把正数a的正平方根叫作a的算术平方根.
课题：3.1.1 平方根的意义及其性质 
1、平方根2、算术平方根3、平方根的性质
基础作业教材第110页习题3.1A 组第1、2、3题能力作业教材第111页习题3.1B 组第8题