5.3二次函数特殊三角形（无答案）

这是一份5.3二次函数特殊三角形（无答案），共44页。

二次函数特殊三角形专题
已知直线与x轴、y轴分别交于点A、B，抛物线经过点A、B，并与x轴交于另一点C，其顶点为P；
1） 求a、k的值
2） 抛物线对称轴上有一点Q，使得△ABQ是以AB为腰的等腰三角形，求点Q的坐标
















已知直线与x轴、y轴分别交于点A、B两点，抛物线经过A、B两点；点P在线段OA上，从点O出发向点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上从点A出发向点B以个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒；
1） 求抛物线解析式
2） 当t为何值时，△APQ为直角三角形














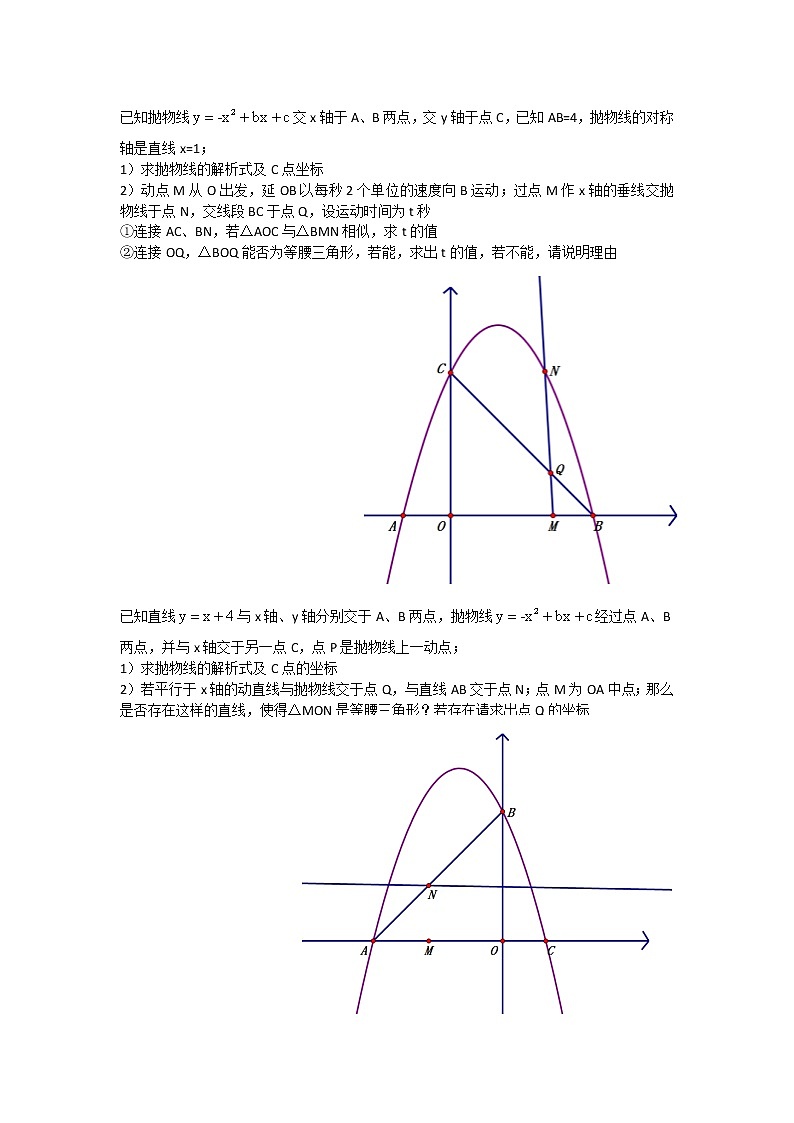
已知抛物线交x轴于A、B两点，交y轴于点C，已知AB=4，抛物线的对称轴是直线x=1；
1）求抛物线的解析式及C点坐标
2）动点M从O出发，延OB以每秒2个单位的速度向B运动；过点M作x轴的垂线交抛物线于点N，交线段BC于点Q，设运动时间为t秒
①连接AC、BN，若△AOC与△BMN相似，求t的值
②连接OQ，△BOQ能否为等腰三角形，若能，求出t的值，若不能，请说明理由
















已知直线与x轴、y轴分别交于A、B两点，抛物线经过点A、B两点，并与x轴交于另一点C，点P是抛物线上一动点；
1） 求抛物线的解析式及C点的坐标
2） 若平行于x轴的动直线与抛物线交于点Q，与直线AB交于点N；点M为OA中点；那么是否存在这样的直线，使得△MON是等腰三角形？若存在请求出点Q的坐标













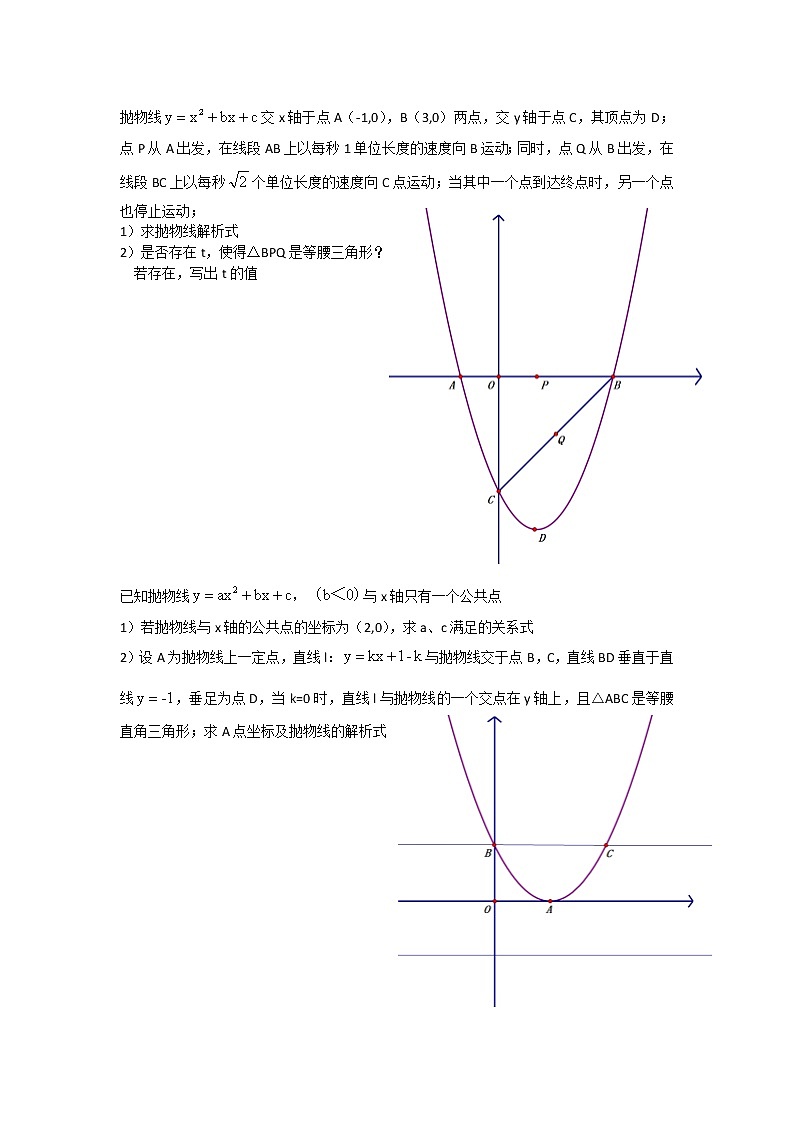
抛物线交x轴于点A（-1,0），B（3,0）两点，交y轴于点C，其顶点为D；点P从A出发，在线段AB上以每秒1单位长度的速度向B运动；同时，点Q从B出发，在线段BC上以每秒个单位长度的速度向C点运动；当其中一个点到达终点时，另一个点也停止运动；
1） 求抛物线解析式
2） 是否存在t，使得△BPQ是等腰三角形？
若存在，写出t的值














已知抛物线与x轴只有一个公共点
1） 若抛物线与x轴的公共点的坐标为（2,0），求a、c满足的关系式
2） 设A为抛物线上一定点，直线l：与抛物线交于点B，C，直线BD垂直于直线，垂足为点D，当k=0时，直线l与抛物线的一个交点在y轴上，且△ABC是等腰直角三角形；求A点坐标及抛物线的解析式












如图，在平面直角坐标系中，抛物线与x轴交于A、B两点,与y轴交于点C，直线L：与抛物线在第四象限的交点为D，若P是y轴负半轴上的一个动点，直线PB与直线L交于点Q，是否存在点P使得△OPQ是等腰三角形？如果存在，求出点P点坐标

















如图，在平面直角坐标系中那个，抛物线的顶点为A，与x轴交于点C，作AB⊥x轴于点B，四边形ABCD为矩形，动点P从点A出发，沿线段AB向终点B运动，同时点Q从C点出发沿线段CD向终点D运动，速度均为每秒1个单位长度，运动时间为t秒，过点P作PE⊥AB交AC于点E，连接EQ，在点P、Q运动过程中，求△CEQ为等腰三角形时t的值















如图，在平面直角坐标系中，抛物线与x轴交于点B、C，与y轴交于点A，过点A的直线与x轴交于D（-2，0），与抛物线交于点E，一动点P在x轴上移动，当
△PAE是直角三角形时，求点P的坐标











如图，在平面直角坐标系中，抛物线与y轴交于点A，与x轴交于B、E两点（点B在点E的左侧），连接AE，P为直线AE上方抛物线上的一点，点P的横坐标为t，是否存在点P，使得△PAE为直角三角形？若存在，求t的值












如图，在平面直角坐标系中，抛物线与x轴交于A、B两点，与y轴交于点C；已知直线L过点E（4，0），点M为直线L上一个动点，若以A、B、M为顶点所作的直角三角形只有三个，求直线L的表达式









抛物线经过点(3,12)和点（-2，-3），与两坐标轴的交点分别为A、B、C，其对称轴为直线l；
1） 求抛物线的表达式
2） P是该抛物线上的点，过点p作l的垂线，垂足为D，E是l上的点，要使以P、D、E为顶点的三角形与△AOC全等，求满足条件的点P和点E的坐标


















抛物线与x轴交于点A（-2,0）和点B（8,0），与y轴交于点C，顶点为D，BC与抛物线的对称轴l交于点E；
1） 求抛物线的表达式
2） 点N是对称轴l右侧抛物线上的动点，在射线ED上是否存在点M使得△MNE与△OBC相似？若存在，请写出M点的坐标











平面直角坐标系中，抛物线与x轴交于点A（-1,0），B(4,0)两点，与y轴交于点C（0，-2）
1） 求抛物线的函数表达式
2） 过点O做直线l∥BC，点P，Q分别为直线l和抛物线上的点。试探究在第一象限是否存在这样的点P，Q，使△PQB∽△CAB，若存在，请写出P的坐标















抛物线与x轴交于A、B两点，点A、B分别位于原点的左右两侧，且BO=3OA=3，过点B的直线与y轴正半轴和抛物线的另一交点分别为C、D，
1） 求b、c的值
2） 点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上；当△ABD与△BPQ相似时，请写出所有满足条件的点Q的坐标















在平面直角坐标系中，直线与x轴、y轴分别交于点B、C，对称轴为x=1的抛物线经过B、C两点且交x轴于另一点A；
1） 求抛物线的解析式
2） 抛物线上是否存在一点Q（点C除外），使以点Q，A，B为顶点的三角形与△ABC相似？若存在请求出点Q坐标














顶点坐标为（2，-1）的抛物线与y轴交于点C（0,3），与x轴交于A、B两点；抛物线对称轴与直线BC交于点D；
1） 求抛物线解析式
2） 点E为直线BC上一动点，过点E作y轴的平行线EF与抛物线交于点F；问是否存在点E使得以D、E、F为顶点的三角形与△BCO相似？若存在，求出点E的坐标


















二次函数的图像交x轴于点A（-1,0），B（4,0），交y轴于点C；动点M从点A出发，以每秒2个单位长度的速度沿射线AB方向运动，过点M作MN⊥x轴交直线BC于点D，连接AC，设运动时间为t秒；
1） 求二次函数表达式
2） 在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求点D的坐标
















已知抛物线的顶点为E（-1,4），且过点A（-3,0），与y轴交于点C，点D是这条抛物线上的一点，它的横坐标为m，且-3＜m＜-1，过点D作DK⊥于x轴，垂足为点K，DK分别交线段AE、AC于点G、H
1） 求抛物线的解析式
2） 当△CGH是等腰直角三角形时，求m的值
















如图，抛物线交x轴于A、B两点，交y轴于点C ；直线经过点A、C；
1） 求抛物线的解析式
2） 点P是抛物线上一动点，过点P作x轴的垂线，交直线AC于点M设点P的横坐标为m；
①连接PC，当△PCM是直角三角形时，求点P的坐标
②作点B关于点C的对称点B1，则平面内存在直线l ，使点M、B、B1到该直线的距离都相等，当点P在y轴右侧的抛物线上，且不与点B重合时，请写出直线L：的解析式；（用含m的式子表示）













如图，已知点A、B分别在x轴和y轴上，且OA = OB = ，点C的坐标是，
AB与OC相交于点G，点P从O出发，以每秒1个单位的速度从O运动到点C，过点P作直线EF∥AB，分别交AO、BO或AC、BC于点E、F；
1） 点G的坐标为
2） 若点P的运动时间为t
①直线EF在四边形OACB内扫过的面积为S，求S与t的函数关系式
②当t为何值时，直线EF平分平行四边形OACB
③设线段OC的中点为Q，连接QE、QF，求当t为何值时，△EFQ为直角三角形












如图一，已知抛物线与x轴交于A、B两点（点A在点B右侧）
与y轴的正半轴交于点C，对称轴与x轴交于点E，作直线BC
1） 求A、B、E的坐标
2） 当以点E为圆心的圆与y轴和直线BC都相切时，求抛物线的解析式
3） 在2）的条件下，如图二，P（t，0）是x轴的负半轴上一点，过点P作y轴的平行线，与直线BC交于点M，与抛物线交于点N，连接CN，将△CMN沿直线CN翻折，点M的对应点为M1 ，是否存在点P，使得点M1恰好落在y轴上，若存在，求点P的坐标














图一 图二
如图一，已知抛物线经过点A（3,0）B（4,4）两点
1） 求抛物线的解析式
2） 将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m的值和D的坐标
3） 如图二，已知点N在抛物线上，且∠NBO = ∠ABO
①求出点N的坐标
②在2）的条件下，直接写出所有满足△POD∽△NOB的点P的坐标












图一 图二
如图，在平面直角坐标系中，抛物线经过点A（-1,0）、点B（4,0）和
点C（0,4）三点
1） 求抛物线的解析式及顶点D的坐标
2） 将1）中的抛物线向下平移个单位，再向左平移h个单位（h＞0）得到新的抛物线；
若新抛物线的顶点在△ABC内，求h的取值范围
3） 点P为线段BC上一动点（点P不与点B、C重合），过点P作x轴的垂线交1）中的抛物线于点Q，当△PQC与△ABC相似时，求△PQC的面积














如图，抛物线与x轴交于点C（ 0 , 4 ），与x轴交于点A、B；
点A的坐标为（ 4 ，0 ）
1） 求该抛物线的解析式
2） 点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ，当△CQE面积最大时，求点Q的坐标
3） 若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2,0）
问：是否存在这样的直线l使得△ODF是等腰三角形？若存在，求点P坐标













如图，二次函数交x轴于点A（-4,0），B（2,0），交y轴于点C（0,6），在y轴上有一点E（0，-2），连接AE
1） 求二次函数的表达式
2） 若点D为抛物线在x轴负半轴上方的一动点，求△ADE面积的最大值
3） 抛物线对称轴上是否存在点P，使△AEP为等腰三角形，若存在，求点P坐标


















如图，已知抛物线（a、b为常数，a≠0）与坐标轴分别交于点A和点B，且点B的坐标为（-3,0），点C的坐标为（1,0），点P是线段AB上方抛物线上的一个动点
1） 求抛物线的解析式
2） 当店P运动到什么位置时，△PAB的面积最大
3） 过点P作x轴的垂线，交线段AB于点D，再过点P作PE∥x轴交抛物线于点E，连接DE，是否存在点P使△PDE为等腰之间三角形？若存在，求点P的坐标












如图，在平面直角坐标系中，已知二次函数的图像经过点A（ -2 , 0 ），
C（0，-6） ，其对称轴为直线 x = 2
1） 求该二次函数的解析式
2） 若直线 将△AOC 的面积分成相等的两部分，求m的值
3） 点B是该二次函数图像与x轴的另一个交点，点D是直线 x = 2上位于x轴下方的动点，点E是第四象限内该二次函数上的动点，点E是第四象限内该二次函数图像上的动点，且位于直线x = 2的右侧；若以点E为直角顶点的△BED与△AOC相似，求点E的坐标










将抛物线C:向下平移6个单位长度得到抛物线C1 ，再将抛物线C1向左平移2个单位长度得到抛物线C2
1) 直接写出抛物线C1 、C2 的解析式
2) 如图一，点A在抛物线C1（对称轴L右侧）上，点B在对称轴L上，△OAB是以OB为斜边的等腰直角三角形，求点A的坐标
3) 如图二，直线与抛物线C2 交于E、F两点，M为线段EF的中点；直线与抛物线C2 交于点G、H两点，N为线段GH的中点；求证：直线MN经过一个定点













图一 图二
如图，抛物线经过点（3 , 12） 和 （ -2 ，-3 ） ，与两坐标轴的交点分别为A、B、C，它的对称轴直线L
1） 求该抛物线的表达式
2） P是该抛物线上的点，过点P作L的垂线，垂足为D，E是L上的点；要使以P、D、E为顶点的三角形与△AOC全等，求满足条件的点P、点E的坐标
















如图一，点A在x轴上，OA = 4 ，将OA绕点O逆时针旋转120°至OB的位置
1） 求经过A、O、B三点的抛物线的函数解析式
2） 在此抛物线的对称轴上是否存在点P使得以P、O、B三点为顶点的三角形时等腰三角形？若存在，求出点P的坐标
3） 如图二，OC = 4，圆A的半径为2 ，点M是圆A上一个动点，求的最小值















图 一 图 二
如图，已知抛物线交x轴于A、C两点，交y轴于点B，且OB = 2 OC
1） 求点A、B、C的坐标及二次函数解析式
2） 在直线AB上方的抛物线上有一动点E，作EG⊥x轴交x轴于点G，交AB于点M，
作EF⊥AB于点F；若点M的横坐标为m，求线段EF的最大值
3） 抛物线对称轴上是否存在点P，使得△ABP为直角三角形，若存在，求P的坐标












如图一，在平面直角坐标系中，直线与抛物线交于A、B两点，其中A（m，0） ，B（4，n） ；该抛物线与y轴交于点C ，与x轴交于另一个点D
1） 求m 、 n 的值及该抛物线的解析式
2） 如图二，若点P为线段AD上的一动点（不与A、D重合）；分别以AP、DP为斜边，在直线AD的同侧作等腰直角△APM和等腰直角△DPN ，连接MN，试确定△MPN面积最大时P点的坐标
3） 如图三连接BD、CD，在线段CD上是否存在点Q，使得以点A、D、Q为顶点的三角形与△ABD相似，若存在，求点Q的坐标
















图一 图二 图三
如图，抛物线经过点A（1,0） 、 B（4,0） 、C（0,3）三点
1） 求抛物线的解析式
2） 在抛物线的对称轴上是否存在点P，使得四边形PAOC的周长最小？若存在，求出四边形PAOC周长的最小值
3） 点Q是线段OB上一动点，连接BC，在线段BC上是否存在点M，使△CQM为等腰三角形且△BQM为直角三角形？若存在，求出点M的坐标















如图，二次函数的图像与x轴交于点A（-1,0）和点B（3,0），交y轴于点N，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接CP，过点P作CP的垂线与y轴交于点E
1） 求该抛物线的函数关系表达式
2） 当点P在线段OB（点P不与O、B重合）上运动至何处时，线段OE的长有最大值
3） 在第四象限的抛物线上任取一点M，连接MN、MB，请问：△MBN的面积是否存在最大值？若存在，求出点M的坐标














如图，抛物线与x轴交于A（-1,0） 、B（3,0） 两点，与x轴交于点C，点D是抛物线的顶点
1） 求抛物线的解析式
2） 点N是y轴负半轴上的一点，且ON = ，点Q在对称轴右侧的抛物线运动，连接QO，QO与抛物线的对称轴交于点M，连接MN ，当MN平分∠OMD时，求点Q的坐标
3） 直线BC交对称轴于点E，P是坐标平面内一点，请直接写出△PCE与△ACD全等时点P的坐标















如图，抛物线交x轴于A（-3,0） ，B（4,0） 两点，与y轴交于点C，连接AC 、BC，点P是第一象限内抛物线上的一个动点，点P的横坐标为m
1） 求此抛物线的表达式
2） 过点P作PM⊥x轴，垂足为点M，PM交BC于点Q，试探究点P在运动过程中是否存在这样的点Q，使得以A、C、Q为顶点的三角形是等腰三角形？若存在，求出点Q坐标
3） 过点P作PN⊥BC，垂足为N，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值？最大值是多少












如图与x轴交于A点，与y轴交于B点，动点P从A点出发，以每秒2个单位的速度沿AO方向向点O匀速运动，同时动点Q从B点出发，以每秒1个单位的速度沿BA方向向点A匀速运动，当一个点停止运动，另一个点也停止运动；连结PQ，设运动时间为t秒（0＜t≤3）
1） 求A、B两点坐标
2） 设△AQP的面积为S，试求出S与t的函数关系式
3） 当t为何值时，△AQP的面积最大
4） 当t为何值时，以点A、P、Q为顶点的三角形与△ABO相似














抛物线过点A（ 3 ，0 ） 、B（ 0 , 2 ） ； 点M（ m ， 0 ）为线段OA上一个动点（点M与点A不重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N
1） 求直线AB的解析式和抛物线的解析式
2） 如果点P是MN的中点，求此时点N的坐标
3） 如果以B、P、N为顶点的三角形与△APM相似，求点M的坐标













如图，在平面直角坐标系中，已知抛物线 ，（a≠0） 的图像经过点B（ 4,0 ）
D（ 5,3 ） ，设它与x轴的另一个交点为A，且△ABD 的面积为3
1） 求该抛物线的表达式
2） 求tan ∠ADB的值
3） 若抛物线与y轴于点C，直线CD交x轴于点E，点P在射线AD上，当△APE与△ABD相似时，求点P的坐标














在平面直角坐标系中，顶点为M的抛物线 ，（ a＞0 ） 经过点A和x轴正半轴上的点B，AO = BO = 2 ，∠AOB = 120°
1） 求这条抛物线的解析式
2） 连结OM，求∠AOM的大小
3） 如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标

















如图，直线与x轴交于点A（ 3,0 ），与y轴交于点B，抛物线经过点A、B
1） 求点B的坐标和抛物线的解析式
2） 点M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P、点N；点M在线段OA上运动，若以点B、P、N为顶点的三角形与△APM相似，求点M的坐标
















如图，一条抛物线顶点为E（ -1 ，4 ） ，且过点A（ - 3 ， 0 ） ，与y轴交于点C，
点D是这条抛物线上一点，它的横坐标为m ，且 ，过点D作DK⊥x轴，垂足为点K，DK分别交线段AE、AC于点G、H
1） 求这条抛物线的解析式
2） 求证：GH = HK
3） 当△CGH是等腰三角形时，求m的值















如图，在平面直角坐标系中，已知抛物线与x轴交于A、B两点，与y轴交于点C ，直线L经过坐标原点O，与抛物线的一个交点为点D，与抛物线的对称轴交于点E，连结CE，已知点A、D的坐标分别为（ -2 ， 0 ） 、（ 6 ， -8 ）
1） 求抛物线的函数表达式及点B和点E的坐标
2） 试探究抛物线上是否存在点F，使△FOE≌△FCE？若存在，求点F坐标
3） 若点P是y轴负半轴上的一个动点，设其坐标为（0，m），直线PB与直线L交于点Q，试探究：当m为何值时，△OPQ是等腰三角形





















在平面直角坐标系中，抛物线与x轴分别交于点A（ 2 ，0 ）、点B（点B在点A右侧），与y轴交于点C，tan∠CBA =
1） 求该抛物线的表达式
2） 设该抛物线的顶点为D，求四边形ACBD的面积
3） 设抛物线上的点在第一象限，△BCE是以BC为一条直角边的直角三角形，求点E坐标








在平面直角坐标系中，抛物线 （a＞0 ）与x轴相交于点A（ -1 ，0 ）和点B ，与y轴交于点C，对称轴为直线 x = 1 ；
1） 求点C的坐标（用含a的代数式表示）
2） 连结AC、BC，若△ABC的面积为6，求此抛物线的表达式
3） 在2）的条件下，点Q为x轴正半轴上一点，点G与点C、点F与点A关于点Q成中心对称，当△CGF为直角三角形时，求点Q的坐标

















如图，已知对称轴为直线x = -1 的抛物线 与x轴交于点A、B两点，与y轴交于点C，其中A（ 1,0 ）
1） 求抛物线的表达式
2） 点D为y轴上一点，若直线BD和直线BC的夹角为15°，求线段CD的长度
3） 设点P为抛物线的对称轴 x = -1 上的一个动点 ，当△BPC为直角三角形时，求点P的坐标













如图，抛物线经过平行四边形ABCD的顶点A（0,3）、B（-1,0）、D（2,3），
抛物线与x轴的另一个交点为点E，经过点E的直线L将平行四边形ABCD分割为面积相等的两部分，与抛物线交于另一点F，点P为直线L上方抛物线上动点，设点P的横坐标为t；
1） 求抛物线的解析式
2） 当t为何值时，△PFE的面积最大？并求最大值的立方根
3） 是否存在点P使△PAE为直角三角心？若存在，求出t的值














抛物线交x轴于A、B两点，交y轴于点C，直线经过点B、C
1） 求抛物线的解析式
2） 过点A的直线交直线BC于点M
①当AM⊥BC时，过抛物线上一动点P（不与点B、C重合），作直线AM的平行线交直线BC于点Q，若以点A、M、P、Q为顶点的四边形是平行四边形，求点P的横坐标
②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，求点M的坐标














如图，二次函数的图像与x轴交于A、B两点，与y轴交于点C，点A的坐标为（ -4 , 0 ） ，P是抛物线上一点（点P与点A、B、C不重合）
1） 求b的值及点B的坐标
2） 设直线PB与直线AC相交于点M，是否存在这样的点P，使得PM：MB = 1:2 ，若存在，求出点P的横坐标
3） 连接AC、BC，判断∠CAB与∠CBA的数量关系









在平面直角坐标系中，直线与x轴交于点B，与y轴交于点C，二次函数的图像经过B、C两点，且与x轴的负半轴交于点A，动点D在直线BC下方的二次函数
1） 求二次函数的表达式
2） 如图一，连接DC、DB，设△BCD的面积为S，求S的最大值
3） 如图二，过点D作DM⊥BC于点M，是否存在点D，使得△CDM的某个角落恰好等于
∠ABC的2倍？若存在，求点D的横坐标










图 一 图 二








若抛物线与x轴、y轴分别交于点A（ 3,0 ）、B（0，-2） ，且过点
C（2，-2）
1） 求抛物线的解析式
2） 若点P为抛物线上第一象限内的点，且 ，求点P的坐标
3） 在抛物线上（AB下方）是否存在点M，使∠ABO = ∠ABM ？若存在，求出点M到y轴的距离














如图，抛物线经过点A（ -1 , 0 ），B（ 4 , 0 ），C（ 0 , 3 ）三点，D为直线BC上方抛物线上一动点，DE⊥BC于点E
1） 求抛物线的解析式
2） 如图一所示，求线段DE长度的最大值
3） 如图二所示，设AB的中点为F ，连接CD、CF，是否存在点D，使得△CDE中有一个角与∠CFO相等，若存在，求点D的横坐标














如图，抛物线与x轴交于A、B两点，与y轴交于点C ，连接AC、BC；点P是第四象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴于点M，PM交BC于点Q，过点P作PE∥AC交x轴于点E，交BC于点F
1） 求A、B、C三点的坐标
2） 在点P运动的过程中，是否存在这样的点Q，使得以A、C、Q为顶点的三角形是等腰三角形？若存在，求出此时点Q的坐标
3） 用含m的代数式表示线段QF的长，并求出m为何值时QF有最大值












如图，在平面直角坐标系中，抛物线F1：与x轴交于点A（，0）和点B ，与y轴交于点C
1） 求抛物线F1的表达式
2） 若将抛物线F1先向左平移1个单位，再向下平移3个单位，得到抛物线F2.若抛物线F1与抛物线F2相交于点D，连接BD、CD、BC
①求点D的坐标
②判断△BCD的形状
3） 在2）的条件下，抛物线F2上是否存在点P，使得△BDP为等腰直角三角形？若存在，求出点P的坐标












在平面直角坐标系中，直线分别与x轴负半轴、y轴正半轴交于点A、C；抛物线经过点A与点C，且与x轴的另一个交点为点B；点D在该抛物线上，且位于直线AC的上方
1） 求上述抛物线的解析式
2） 连结BC、BD ，且BD交AC于点E，如果△ABE的面积与△ABC的面积之比为4:5，
求tan∠DBA
3） 过点D作DF⊥AC，垂足为点F，连结CD，若△CFD与△AOC相似，求点D的坐标






二次函数的图像与x轴交于A、B两点，与y轴交于点C，OB = OC ；点D在函数图像上，CD∥x轴，且CD = 2 ，直线L是抛物线的对称轴，E是抛物线的顶点
1） 求b、c的值
2） 如图一，连结BE，线段OC上点F关于直线L的对称点G恰好在线段BE上，
求点F的坐标
3） 如图二，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M，与抛物线交于点N，试问：抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？如果存在，求点Q的坐标


















图一 图二

如图，二次函数的图像与x轴交于A（ 3,0 ）、B（ -1 ， 0 ） ，与y轴交于点C ，若点P、Q同时从点A出发，都以每秒1个单位长度的速度分别沿AB、AC边运动，其中一点到达端点时，另一点也随即停止运动
1） 求该二次函数的解析式
2） 当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E，使得以A、E、Q为顶点的三角形是等腰三角形，若存在，求出点E的坐标
3） 当P、Q运动t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请判定四边形APDQ的形状，并求出点D的坐标





















如图，在平面直角坐标系中，的图像与x轴交于A、B两点，与y轴交于点C，点P是直线AC上方的抛物线上一动点，使△ACP的面积为整数的点P有几个？











如图，在平面直角坐标系中，抛物线与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴与抛物线交于点P，与x轴交于点G，与直线BC交于点M，连接PB；问抛物线上是否存在点Q使得△QMB与△PMB的面积相等？若存在，求出点Q坐标
















如图，在平面直角坐标系中，抛物线与x轴正半轴交于点A，与y轴交于点B；设Q为抛物线上一动点，若抛物线上有且只有三个点Q使得，求m的值



















如图，在平面直角坐标系中，抛物线与x轴交于A、B两点，点P为对称轴右侧、x轴上方抛物线上一点，过点P作PE⊥x轴于点E，以AE、PE为邻边作AEPC，PC交抛物线于点D，连接CE、BD、AP，CE与AP交于点F，DB交PE于点H，交AP于点G；若，求点P的坐标















如图，在平面直角坐标系中，抛物线，点M的坐标为（7,0），过抛物线上x轴下方的一点D作DE∥x轴，与抛物线的另一个交点为点E，作DF⊥x轴于点F，已知在线段DF上存在点P，使得△PED≌△MPF，求所有满足条件的点D的横坐标的和






如图，在平面直角坐标系中，抛物线与x轴交于A、B两点，与y轴交于点C，直线BC与抛物线的对称轴交于点D，该抛物线的顶点为P，连接PA、AD；在y轴或抛物线的对称轴上是否存在一点Q，使得以Q、C、D为顶点的三角形与△ADP全等？若存在，求点Q的坐标












如图，在平面直角坐标系中，抛物线与x轴交于A、B两点，与y轴交于点C，过点A作AP∥CB交抛物线于点P，在x轴上方的抛物线上有一动点M，过点M作MG⊥x轴于点G，若以AMG为顶点的三角形与△PCA相似，求点M的坐标






















如图，在平面直角坐标系中，抛物线与x轴交于A、B两点，已知点
D（1，n）在抛物线上，过点A且平行于BD的直线交抛物线于另一点E，若点P在x轴上，是否存在这样的点P，使得以点P、B、D为顶点的三角形与△AEB相似？请说明理由















如图，在平面直角坐标系中，抛物线与y轴交于点A，已知点Q（7，n）在抛物线上，抛物线的顶点为D，连接AQ交抛物线的对称轴于点E，点E关于点D的对称点为点F，抛物线的对称轴交x轴于点G，连接AF、FQ分别交x轴于点B、C；点P为点A下方y轴上一动点，是否存在点P，使得△AFP与△FDQ相似？若存在，求点P的坐标




















在平面直角坐标系中，过点A（3,4）的抛物线与x轴交于点B（-1,0），与y轴交于点C，过点A作AD⊥x轴于点D
1） 求抛物线的解析式
2） 如图一，点P是直线AB上方抛物线上的一个动点，连接PD交AB于点Q，连接AP，当时，求点P的坐标
3） 如图二，点G是线段OC上一个动点，连接DG，过点G作GM⊥DG交AC于点M，过点M作射线MN，使∠NMG = 60°，交射线GD于点N；过点G作GH⊥MN于点H，连接BH，求线段BH的最小值













图一 图二

如图，在平面直角坐标系中，抛物线与x轴交于点A、B（点A在点B的左侧），交y轴于点C，点D为抛物线的顶点，对称轴与x轴交于点E
1） 连接BD，点M是线段BD上一动点（点M不与端点B、D重合），过点M作MN⊥BD，交抛物线于点N（点N在对称轴的右侧），过点N作NH⊥x轴，垂足为点H，交BD于点F；点P是线段OC上以动点，当MN取最大值时，求的最小值
2） 在1）中，当MN取得最大值，的最小值时，把点P向上平移个单位得到点Q，连接AQ，把△AOQ绕点O顺时针旋转一定的角度x（0°＜x＜360°），得到△A`OQ`，其中边A`Q`交坐标轴于点G，在旋转过程中，是否存在一点G，使得∠Q` = ∠Q`OG？













如图已知抛物线与x轴交于点A，B（3,0），与y轴交于点C（0,3）直线L经过B、C两点，抛物线顶点为E
1） 求抛物线和直线的解析式
2） 判断△BCD的形状并说明理由
3） 如图二，若点E是线段BC上方的抛物线上的一个动点，过点E作EF⊥x轴于点F，EF交线段BC于点G，当△ECG是直角三角形时，求点E的坐标










图 一 图 二

如图，二次函数的图像与x轴交于两点，分别是点A（1,0）和点B（4,0）
1） 求二次函数的解析式
2） 若这个抛物线的对称轴交x轴于点E，点F是位于x轴上方抛物线上一点，FC∥x轴、与对称轴右侧的抛物线交于点C，且四边形OECF是平行四边形，求点C的坐标
3） 在2）的条件下，抛物线的对称轴是否存在点P，使得△OCP是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由












如图一，在平面直角坐标系中，抛物线与x轴分别交于点A、B，点A坐标为（-3,0），与y轴交于点C，抛物线的顶点E的坐标为（-1,4），对称轴交x轴于点F，连接AC、AE、CE
1） 请直接写出这条抛物线和直线AC的解析式
2） 判断△ACE的形状
3） 如图二，点D是抛物线上一动点，它的横坐标为m ， 且 -3 ＜m＜ -1 ，过点D作DK⊥x轴于点K，KD分别交线段AE、AC于点G、H
①在点D的运动过程中，DG、GH、HK这三条线段能否相等？若相等，请求出点D的坐标，若不相同，请说明理由
②在①的条件下，判断CG与AE的数量关系，并直接写出结论
















如图，已知抛物线与x轴交于A（-4,0）、B（1,0）两点，与y轴交于点C，动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动，过点D作x轴的垂线，交△ABC的另一边于点E，将△ADE沿DE折叠，使点A落在点F处，设点D的运动时间为t秒
1） 求抛物线的解析式及顶点坐标
2） N为抛物线上的点（点N不与点C重合）且满足，直接写出点N的坐标
3） 是否存在某一时刻t，使得△EFC为直角三角形？若存在，求出t的值












抛物线过点A（2,3）、B（4,3）、C（6，-5）三点
1） 求抛物线的解析式
2） 如图一，抛物线上一点D在线段AC的上方，DE⊥AB交AC于点E，若满足=，求点D的坐标
3） 如图二，F为抛物线顶点，过点A作直线L上运动，点Q在x轴上运动，是否存在这样的点P、Q，使得以点B、P、Q为顶点的三角形与△ABF相似？若存在，求点P、Q的坐标，并求出此时△BPQ的面积













如图一，经过点O的抛物线（a≠0）x轴交于另一点A（，0），在第一象限内与直线交于点B（2，t）
1） 求抛物线的解析式
2） 在第四象限内的抛物线上有一点C，满足以点B、O、C为顶点的三角形的面积为2，求点C的坐标
3） 如图二，若点M在这条抛物线上，且∠MBO = ∠ABO ，在2）的条件下，是否存在点P，使得△POC∽△MOB？若存在，求出点P的坐标；若不存在，请说明理由













已知抛物线经过点A（-2,0）、B（0，-4），与x轴交于另一点C，连接BC
1） 求抛物线的解析式
2） 如图，点P是第一象限内抛物线上一点，且，求证：AP∥BC
3） 在抛物线上是否存在点D，直线BD交x轴于点E，使△ABE与以A、B、C、E中的三点为顶点的三角形相似？若存在，请求出点D的坐标，若不存在，请说明理由
















如图，已知直线与抛物线相交于A（-1,0）、B（4，m）两点，抛物线交y轴于点C（0，），交x轴正半轴于点D，抛物线的顶点为点M
1） 求抛物线的解析式及点M的坐标
2） 设点P为直线AB下方的抛物线上一动点，当△PAB的面积最大时，此时△PAB的面积及点P的坐标
3） 点Q为x轴上一动点，点N是抛物线上一点，当△QMN∽△MAD ，求点Q的坐标











抛物线L：经过点A（0,1），与它的对称轴直线交于点B
1） 求抛物线L的解析式
2） 如图一，过定点的直线（k＜0）与抛物线L交于点M，N，若△BMN的面积等于1，求k的值
3） 如图二，将抛物线L向上平移m（m＞0）个单位长度得到抛物线L1 ，抛物线L1与y轴交于点C，过点C作y轴的垂线交抛物线L1于另一点D；点F为抛物线L1的对称轴与x轴的交点，点P为线段OC上一点，若△PCD与△POF相似，并且符合条件的点P恰好有2个，求m的值及相应的点P的坐标














如图，抛物线交x轴于A、B两点，交y轴于点C，直线经过点A、C
1） 求抛物线的解析式
2） 点P是抛物线上一动点，过点P作x轴的垂线，交直线AC于M，设点P的横坐标为m
①当△PCM是直角三角形时，求点P的坐标
②作点B关于点C的对称点B`，则平面内存在直线L，使点M、B、B`到该直线的距离都相等；当点P在y轴右侧的抛物线上且与点B不重合时，请写出直线L：的解析式












如图，抛物线与x轴交于A（-1 , 0）、B（3,0）两点，与y轴交于点C，点D是抛物线的顶点
1） 求抛物线的解析式
2） 点N是y轴负半轴上的一点，且ON = ，点Q在对称轴右侧的抛物线上运动，连接QO，QO与抛物线的对称轴交于点M，连接MN，当MN平分∠OMD时，求点Q的坐标
3） 如图二，直线BC交对称轴于点E，P是坐标平面内一点，求△PCE与△ACD全等时点P的坐标














如图一，平面直角坐标系中，直线L1：与直线L2：相交于点D，点A是直线L2上的动点，过点A作AB⊥L1于点B，点C的坐标为（0,3），连接AC、BC；设点A的纵坐标为t，△ABC的面积为S
1） 当t = 2 时，请直接写出点B的坐标
2） S关于t的函数解析式为S = ，其图像如图二所示，结合两图，求出a与b的值
3） 在L2上是否存在点A，使得△ABC是直角三角形？若存在，请求出此时点A的坐标和△ABC的面积
















如图，已知抛物线经过两点A（-1,0）、B（3,0）、C是抛物线与y轴的交点
1） 求抛物线的表达式
2） 点P（m，n）在平面直角坐标系第一象限内的抛物线上运动，设△PBC的面积为S，求S关于m的函数表达式（指出自变量m的取值范围）和S的最大值
3） 点M在抛物线上运动，点N在y轴上运动，是否存在点M、点N，使得∠CMN = 90°，且△CMN与△OBC相似，如果存在，请求出点M和点N的坐标