湖北省仙桃市八年级下学期数学期末考试试卷

这是一份湖北省仙桃市八年级下学期数学期末考试试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
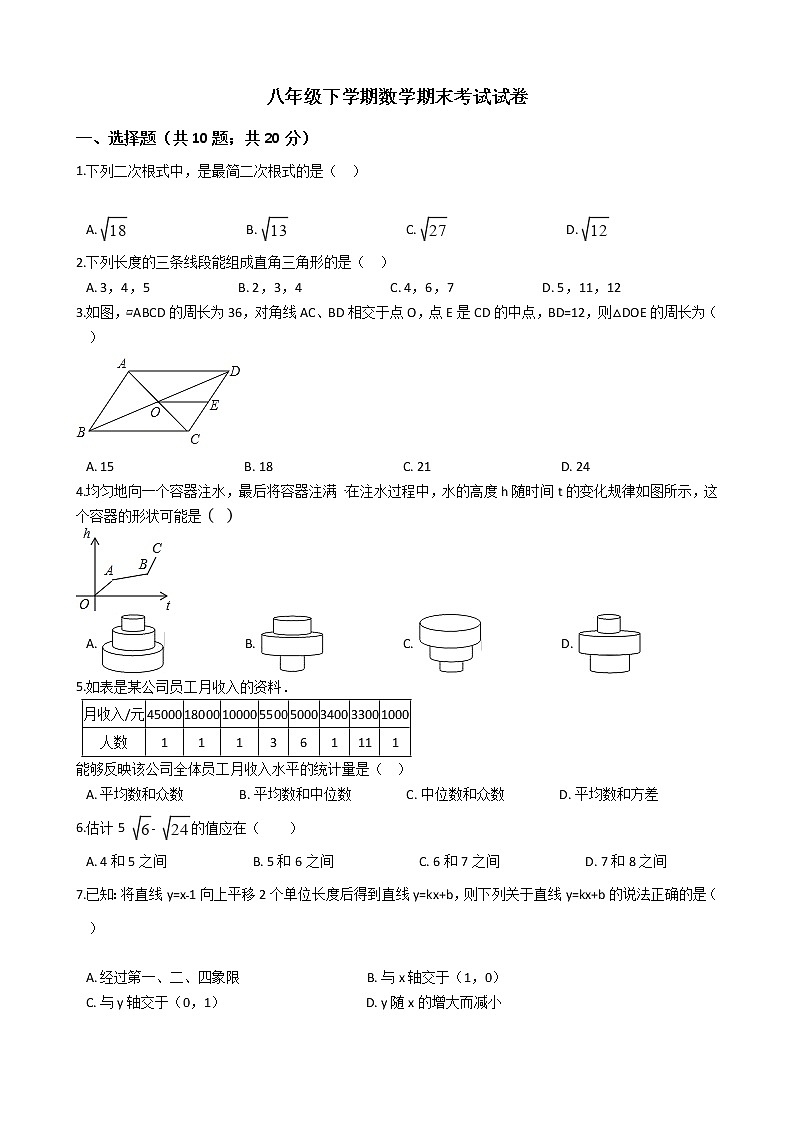
1.下列二次根式中，是最简二次根式的是（ ）

A. B. C. D.
2.下列长度的三条线段能组成直角三角形的是（ ）
A. 3，4，5 B. 2，3，4 C. 4，6，7 D. 5，11，12
3.如图，▱ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（ ）
A. 15 B. 18 C. 21 D. 24
4.均匀地向一个容器注水，最后将容器注满 在注水过程中，水的高度h随时间t的变化规律如图所示，这个容器的形状可能是
A. B. C. D.
5.如表是某公司员工月收入的资料．
能够反映该公司全体员工月收入水平的统计量是（ ）
A. 平均数和众数 B. 平均数和中位数 C. 中位数和众数 D. 平均数和方差
6.估计5 ﹣ 的值应在（ ）
A. 4和5之间 B. 5和6之间 C. 6和7之间 D. 7和8之间
7.已知：将直线y=x﹣1向上平移2个单位长度后得到直线y=kx+b，则下列关于直线y=kx+b的说法正确的是（ ）

A. 经过第一、二、四象限 B. 与x轴交于（1，0）
C. 与y轴交于（0，1） D. y随x的增大而减小
8.如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E，F，连接PB，PD．若AE=2，PF=8．则图中阴影部分的面积为（ ）
A. 10 B. 12 C. 16 D. 18
9.若直线y＝kx+k+1经过点（m，n+3）和（m+1，2n﹣1），且0＜k＜2，则n的值可以是（ ）
A. 4 B. 5 C. 6 D. 7
10.如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F点，连结CP并延长CP交AD于Q点．给出以下结论：
①四边形AECF为平行四边形；②∠PBA=∠APQ；③△FPC为等腰三角形；④△APB≌△EPC．其中正确结论的个数为（ ）
A. 1 B. 2 C. 3 D. 4
二、填空题（共8题；共11分）
11.函数y= 的自变量x的取值范围是________．
12.小王参加某企业招聘测试，他的笔试、面试、技能操作得分分别为85分，80分，90分，若依次按照2：3：5的比例确定成绩，则小王的成绩________分.
13.已知E是正方形ABCD的对角线AC上一点，AE=AD，过点E作AC的垂线，交边CD于点F，那么∠FAD=________ 度.
14.如图，在平面直角坐标系中，点A、B的坐标分别为（1，3）、（n，3），若直线y=2x与线段AB有公共点，则n的值可以为________．（写出一个即可）
15.在矩形ABCD中，AB＝4，AD＝3，矩形内部有一动点P满足S矩形ABCD＝3S△PAB ， 则PA+PB的最小值为________.
16.如图，一次函数y=﹣x﹣2与y=2x+m的图象相交于点P（n，﹣4），则关于x的不等式组 的解集为________．

17.如图，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G．若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为________．
18.观察下列各式：
，
，
，
……
请利用你所发现的规律，
计算 + + +…+ ，其结果为________．
三、解答题（共7题；共42分）
19.计算：
（1）2 ﹣6 +3 ；
（2）（1+ ）（ ﹣ ）+（ ﹣ ）× .
20.如图，在Rt△ABC中，∠C＝90°.
（1）求作：△ABC的一条中位线，与AB交于D点，与BC交于E点.（保留作图痕迹，不写作法）
（2）若AC＝6，AB＝10，连结CD，则DE＝________，CD＝_________.
21.为了参加“仙桃市中小学生首届诗词大会”，某校八年级的两班学生进行了预选，其中班上前5名学生的成绩（百分制）分别为：八（1）班 86，85，77，92，85；八（2）班 79，85，92，85，89.通过数据分析，列表如下：
（1）直接写出表中a，b，c，d的值；
（2）根据以上数据分析，你认为哪个班前5名同学的成绩较好？说明理由.
22.文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元，甲种图书每本的售价是乙种图书每本售价的1.4倍，若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.

（1）甲乙两种图书的售价分别为每本多少元？
（2）书店为了让利读者，决定甲种图书售价每本降低3元，乙种图书售价每本降低2元，问书店应如何进货才能获得最大利润？（购进的两种图书全部销售完.）

23.如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F.
（1）求证：四边形ADEF为平行四边形；
（2）当点D为AB中点时，判断▱ADEF的形状；
（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由.
24.如图，已知点A（6，0），B（8，5），将线段OA平移至CB，点D（x，0）在x轴正半轴上（不与点A重合），连接OC，AB，CD，BD.
（1）求对角线AC的长；
（2）△ODC与△ABD的面积分别记为S1 ， S2 ， 设S＝S1﹣S2 ， 求S关于x的函数解析式，并探究是否存在点D使S与△DBC的面积相等，如果存在，请求出x的值（或取值范围）；如果不存在，请说明理由.
25.在菱形ABCD中，∠ABC＝60°，P是射线BD上一动点，以AP为边向右侧作等边△APE，连接CE.
（1）如图1，当点P在菱形ABCD内部时，则BP与CE的数量关系是________，CE与AD的位置关系是________.
（2）如图2，当点P在菱形ABCD外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由；
（3）如图2，连接BE，若AB＝2 ，BE＝2 ，求AP的长.
答案解析部分
一、选择题
1.【解析】【解答】解：A、 不是最简二次根式，不符合题意；
B、 是最简二次根式，符合题意；
C、 不是最简二次根式，不符合题意；
D、 不是最简二次根式，不符合题意，
故答案为：B
【分析】满足下列两个条件的二次根式,叫做最简二次根式：(1)被开方数的因数是整数,因式是整式；(2)被开方数中不含能开得尽方的因数或因式．上述两个条件同时具备(缺一不可)的二次根式叫最简二次根式。对各选项逐一判断可求解。
2.【解析】【解答】A、∵32+42=52 ， ∴三条线段能组成直角三角形，故A符合题意；
B、∵22+32≠42 ， ∴三条线段不能组成直角三角形，故B不符合题意；
C、∵42+62≠72 ， ∴三条线段不能组成直角三角形，故C不符合题意；
D、∵52+112≠122 ， ∴三条线段不能组成直角三角形，故D不符合题意；
故答案为：A．
【分析】根据勾股定理的逆定理，若已知的线段满足a2+b2=c2 ， 则可判断为直角三角形。
3.【解析】【解答】解：∵平行四边形ABCD的周长为36，
∴BC+CD=18，
∵OD=OB，DE=EC，
∴OE+DE= （BC+CD）=9，
∵BD=12，
∴OD= BD=6，
∴△DOE的周长为9+6=15，
故答案为：A．
【分析】根据平行四边形性质得出BC+CD=18，OD= BD=6，根据三角形的中位线定理得出OE+DE= （BC+CD）=9，从而根据三角形周长的计算方法，得出答案。
4.【解析】【解答】解：注水量一定，从图中可以看出，OA上升较快，AB上升较慢，BC上升最快，
由此可知这个容器下面容积较大，中间容积最大，上面容积最小，
故答案为：D
【分析】观察h与t的函数图像，可得出OA上升较快，AB上升较慢，BC上升最快，因此可得出这个容器下面容积较大，中间容积最大，上面容积最小，可得出答案。
5.【解析】【解答】解：该公司员工月收入的众数为3300元，在25名员工中有13人这此数据之上，
所以众数能够反映该公司全体员工月收入水平；
因为公司共有员工1+1+1+3+6+1+11+1=25人，
所以该公司员工月收入的中位数为5000元；
由于在25名员工中在此数据及以上的有12人，
所以中位数也能够反映该公司全体员工月收入水平；
故答案为：C．
【分析】求出中位数和众数进行分析：中位数也能够反映该公司全体员工月收入水平，众数能够反映该公司全体员工月收入水平，平均数受极端值的影响，因此可得出答案。
6.【解析】【解答】解：5 − ＝5 −2 ＝3 ＝ ，
∵7＜ ＜8，
∴5 − 的值应在7和8之间，
故答案为：D.
【分析】先合并后，再根据无理数的估计解答即可.
7.【解析】【解答】将直线y=x﹣1向上平移2个单位长度后得到直线y=x﹣1+2=x+1，
A、直线y=x+1经过第一、二、三象限，不符合题意；
B、直线y=x+1与x轴交于（﹣1，0），不符合题意；
C、直线y=x+1与y轴交于（0，1），符合题意；
D、直线y=x+1，y随x的增大而增大，不符合题意，
故答案为：C．
【分析】根据直线的几何变换规律得出直线y=x﹣1向上平移2个单位长度后的直线的解析式，再根据一次函数的图像与系数的关系，一次函数的性质，一次函数与坐标轴的交点特点即可一一解决。
8.【解析】【解答】解：作PM⊥AD于M，交BC于N．
则有四边形AEPM，四边形DFPM，四边形CFPN，四边形BEPN都是矩形，
∴S△ADC=S△ABC ， S△AMP=S△AEP ， S△PBE=S△PBN ， S△PFD=S△PDM ， S△PFC=S△PCN ，
∴S△DFP=S△PBE= ×2×8=8，
∴S阴=8+8=16，
故答案为：C．
【分析】作PM⊥AD于M，交BC于N．则有四边形AEPM，四边形DFPM，四边形CFPN，四边形BEPN都是矩形，根据矩形的对角线将矩形分成两个面积相等的三角形得出S△ADC=S△ABC ， S△AMP=S△AEP ， S△PBE=S△PBN ， S△PFD=S△PDM ， S△PFC=S△PCN ， 故S△DFP=S△PBE，从而得出答案。
9.【解析】【解答】解：依题意得： ，
∴k=n-4，
∵0＜k＜2，
∴0＜n-4＜2，
∴4＜n＜6，
故答案为：B.
【分析】根据题意列方程组得到k=n-4，由于0＜k＜2，于是得到0＜n-4＜2，即可得到结论.
10.【解析】【解答】①如图，EC，BP交于点G；
∵点P是点B关于直线EC的对称点，∴EC垂直平分BP，∴EP=EB，∴∠EBP=∠EPB．
∵点E为AB中点，∴AE=EB，∴AE=EP，∴∠PAB=∠PBA．
∵∠PAB+∠PBA+∠APB=180°，即∠PAB+∠PBA+∠APE+∠BPE=2（∠PAB+∠PBA）=180°，∴∠PAB+∠PBA=90°，∴AP⊥BP，∴AF∥EC；
∵AE∥CF，∴四边形AECF是平行四边形，故①正确；
②∵∠APB=90°，∴∠APQ+∠BPC=90°，由折叠得：BC=PC，∴∠BPC=∠PBC．
∵四边形ABCD是矩形，∴∠ABC=∠ABP+∠PBC=90°，∴∠ABP=∠APQ，故②正确；
③∵AF∥EC，∴∠FPC=∠PCE=∠BCE．
∵∠PFC是钝角，当△BPC是等边三角形，即∠BCE=30°时，才有∠FPC=∠FCP，如右图，△PCF不一定是等腰三角形，故③不正确；
④∵AF=EC，AD=BC=PC，∠ADF=∠EPC=90°，∴Rt△EPC≌△FDA（HL）．
∵∠ADF=∠APB=90°，∠FAD=∠ABP，当BP=AD或△BPC是等边三角形时，△APB≌△FDA，∴△APB≌△EPC，故④不正确；
其中正确结论有①②，2个．
故答案为：B
【分析】①如图，EC，BP交于点G；根据对折的性质得出EC垂直平分BP，根据垂直平分线的性质得出EP=EB，根据等边对等角得出∠EBP=∠EPB．根据中点的定义得出AE=EB，故AE=EP根据等边对等角得出∠PAB=∠PBA．根据三角形的内角和得出∠PAB+∠PBA=90°，故AP⊥BP根据同一平面内垂直于同一直线的两条直线互相平行得出AF∥EC；根据两组对边分别平行的四边形是平行四边形得出四边形AECF是平行四边形，故①正确；②根据平角的定义得出∠APQ+∠BPC=90°，由折叠得：BC=PC，故∠BPC=∠PBC．根据正方形的性质得出∠ABC=∠ABP+∠PBC=90°根据等角的余角相等得出∠ABP=∠APQ，故②正确；③根据二直线平行内错角相等及折叠的性质得出∠FPC=∠PCE=∠BCE．∠PFC是钝角，当△BPC是等边三角形，即∠BCE=30°时，才有∠FPC=∠FCP，如右图，△PCF不一定是等腰三角形，故③不正确；④利用HL判断出Rt△EPC≌△FDA，∠ADF=∠APB=90°，∠FAD=∠ABP，当BP=AD或△BPC是等边三角形时，△APB≌△FDA，故△APB≌△EPC，故④不正确。
二、填空题
11.【解析】【解答】解：根据题意得x≠0且1﹣2x≥0， 所以x≤ 且x≠0．
故答案为x≤ 且x≠0
【分析】根据分母不为零和被开方数不小于零得到x≠0且1﹣2x≥0，然后求出两不等式的公共解即可．
12.【解析】【解答】解：根据题意得：
85× +80× +90× =17+24+45=86（分），
答：小王的成绩是86分.
故答案为86.
【分析】根据加权平均数的公式计算即可求解.
13.【解析】【解答】解：如图，
在Rt△AEF和Rt△ADF中，
∴Rt△AEF≌Rt△ADF，
∴∠DAF=∠EAF，
∵四边形ABCD为正方形，
∴∠CAD=45°，
∴∠FAD=22.5°．
故答案为：22.5．
【分析】根据正方形的性质可得∠DAC=45°，再由AD=AE易证△ADF≌△AEF，求出∠FAD．
14.【解析】【解答】∵直线y=2x与线段AB有公共点，
∴2n≥3，
∴n≥ ，
故答案为：2．
【分析】由点A、B两点坐标的特点：纵坐标相等，可得出线段AB∥x轴，因此直线y=2x与线段AB有公共点，建立不等式2n≥3，求解即可。
15.【解析】【解答】解：设△ABP中AB边上的高是h.
∵S矩形ABCD=3S△PAB ，
∴ AB•h= AB•AD，
∴h= AD=2，
∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离.
在Rt△ABE中，∵AB=4，AE=2+2=4，
∴BE= ，
即PA+PB的最小值为4 .
故答案为：4 .
【分析】首先由S矩形ABCD=3S△PAB ， 得出动点P在与AB平行且与AB的距离是2的直线l上，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离.然后在直角三角形ABE中，由勾股定理求得BE的值，即PA+PB的最小值.
16.【解析】【解答】∵一次函数y=﹣x﹣2的图象过点P（n，﹣4），
∴﹣4=﹣n﹣2，解得n=2，
∴P（2，﹣4），
又∵y=﹣x﹣2与x轴的交点是（﹣2，0），
∴关于x的不等式组 的解集为
故答案为：
【分析】先把点P的坐标代入y=-x-2,求出n的值，再找出直线y=2x+m在直线y=-x-2下方且都在x轴下方的部分对应的自变量的取值范围即可。

17.【解析】【解答】解：∵阴影部分的面积与正方形ABCD的面积之比为2：3，
∴阴影部分的面积为 ×9=6，
∴空白部分的面积为9﹣6=3，
由CE=DF，BC=CD，∠BCE=∠CDF=90°，可得△BCE≌△CDF，
∴△BCG的面积与四边形DEGF的面积相等，均为 ×3= ，
设BG=a，CG=b，则 ab= ，
又∵a2+b2=32 ，
∴a2+2ab+b2=9+6=15，
即（a+b）2=15，
∴a+b= ，即BG+CG= ，
∴△BCG的周长= +3，
故答案为： +3．
【分析】由阴影部分的面积与正方形ABCD的面积之比为2：3，可求出阴影部分的面积和空白部分的面积，再证明△BCE≌△CDF，可证得△BCG的面积与四边形DEGF的面积相等，设BG=a，CG=b，利用勾股定理及三角形的面积公式，建立方程组，可求出BG+CG的值，继而可求出△BCG的周长。
18.【解析】【解答】解：由题意可得：
+ + +…+
= +1+ +1+ +…+1+
=9+（1﹣ + ﹣ + ﹣ +…+ ﹣ ）
=9+
=9 ．
故答案为：9 ．
【分析】根据题意首先将各个加数的根号去掉，然后根据加法的交换律和结合律，让整数部分相加，分数部分相加，分数部分相加的时候利用,进行简便运算即可算出结果。
三、解答题
19.【解析】【分析】（1）直接利用二次根式的性质化简得出答案；（2）首先利用二次根式乘法运算法则化简，进而计算得出答案.
20.【解析】【解答】解：（2）∵DE是△ABC的中位线，
∴DE= AC，
∵AC=6，
∴DE=3，
∵AB=10，CD是Rt△斜边上的中线等于斜边的一半，
∴CD=5，
故答案为：3，5.
【分析】（1）作边AB的中垂线，交AB于D，过点D作DE⊥BC，垂足为E，连接DE即可；
（2）根据三角形的中位线定理直接得出DE的长，再根据直角三角形斜边上的中线等于斜边的一半，求出CD.

21.【解析】【分析】（1）根据平均数、中位数、众数的概念解答， 根据方差计算公式，求出八（1）班的方差即可；
（2）先根据方差计算公式，求出八（1）班的方差，结合平均数、中位数、众数与方差的意义求解即可.


22.【解析】【分析】（1）此题的等量关系是：甲种图书每本的售价=乙种图书每本售价×1.4；若用1680元在文美书店可购买甲种图书的本数=用1400元购买乙种图书的本数-10，设未知数，列方程求解即可。
（2）设甲种图书进货 a 本，总利润 w 元，根据题意列出W与a的函数解析式，根据一次函数的性质及a的取值范围（用不多于20000元购进甲乙两种图书共1200本进行销售），即可求解。
23.【解析】【分析】(1)根据平行线的性质得到∠BDE=∠A，根据题意得到∠DEF=∠BDE，根据平行线的判定定理得到AD∥EF，根据平行四边形的判定定理证明；(2)根据三角形中位线定理得到DE= AC，得到AD=DE，根据菱形的判定定理证明；(3)根据等腰三角形的性质得到AE⊥EG，根据有一个角是直角的平行四边形是矩形证明.
24.【解析】【分析】（1）根据平移的性质可以求得点C的坐标，然后根据两点间的距离公式即可求得AC的长；（2）根据题意，可以分别表示出S1 ， S2 ， 从而可以得到S关于x的函数解析式，由图和题目中的条件可以求得△CDB的面积，从而可以求得满足条件的点D的坐标，本题得以解决.
25.【解析】【解答】(1)解：BP=CE，CE⊥AD.
理由：∵菱形ABCD中，∠ABC=60°
∴AB=BC=CD=AD，∠ADC=∠ABC=60°
∴△ABC、△ACD是等边三角形
∴AB=AC，AC=CD，∠BAC=∠ACD=60°
∵△APE是等边三角形
∴AP=AE，∠PAE=60°
∴∠BAC-∠PAC=∠PAE-∠PAC
即∠BAP=∠CAE，
∴△BAP≌△CAE（SAS）
∴BP=CE，∠ABP=∠ACE
∵BD平分∠ABC
∴∠ACE=∠ABP= ∠ABC=30°
∴CE平分∠ACD
∴CE⊥AD.
故答案为BP=CE，CE⊥AD.
【分析】（1）由菱形ABCD和∠ABC=60°可证△ABC与△ACD是等边三角形，由等边△APE可得AP=AE，∠PAE=∠BAC=60°，减去公共角∠PAC得∠BAP=∠CAE，根据SAS可证得△BAP≌△CAE，故有BP=CE，∠ABP=∠ACE.由菱形对角线平分一组对角可证∠ABP=30°，故∠ACE=30°即CE平分∠ACD，由AC=CD等腰三角形三线合一可得CE⊥AD.（2）结论不变.证明过程同（1）.（3）在Rt△AOP中，求出OA，OP即可解决问题.月收入/元
45000
18000
10000
5500
5000
3400
3300
1000
人数
1
1
1
3
6
1
11
1
班级
平均分
中位数
众数
方差
八（1）
85
b
85
d
八（2）
a
85
c
19.2