初中数学沪科版八年级上册14.2 三角形全等的判定优质课件ppt

这是一份初中数学沪科版八年级上册14.2 三角形全等的判定优质课件ppt，共13页。PPT课件主要包含了复习旧知，探究新知，CFAE已知，根据步骤填空，课堂小结，全等知识的综合应用，随堂练习等内容，欢迎下载使用。
我们学过三角形全等的判定有
边边边：三边分别相等的两个三角形全等（可简写成“SSS”)边角边:两边和它们的夹角分别相等两个三角形全等（可简写成“SAS”)角边角:两角和它们的夹边分别相等的两个三角形全等（可简写成“ASA”)角角边:两角和其中一角的对边分别相等的两个三角形全等（可简写成“AAS”)斜边、直角边：斜边和一条直角边分别相等的两个直角三角形全等（可简写成“HL”)
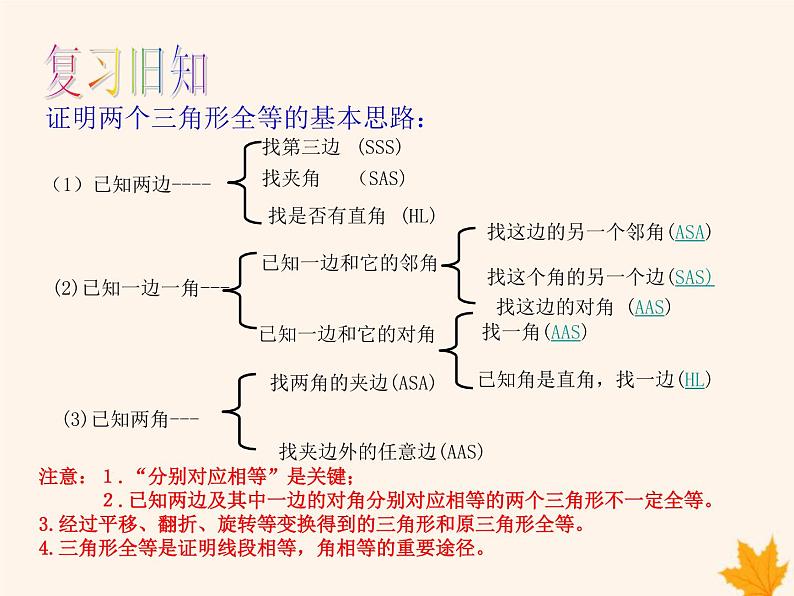
证明两个三角形全等的基本思路：
（1）已知两边----
(2)已知一边一角---
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找这边的对角 (AAS)
已知角是直角，找一边(HL)
找两角的夹边(ASA)
找夹边外的任意边(AAS)
注意：１.“分别对应相等”是关键；　　　２.已知两边及其中一边的对角分别对应相等的两个三角形不一定全等。3.经过平移、翻折、旋转等变换得到的三角形和原三角形全等。4.三角形全等是证明线段相等，角相等的重要途径。
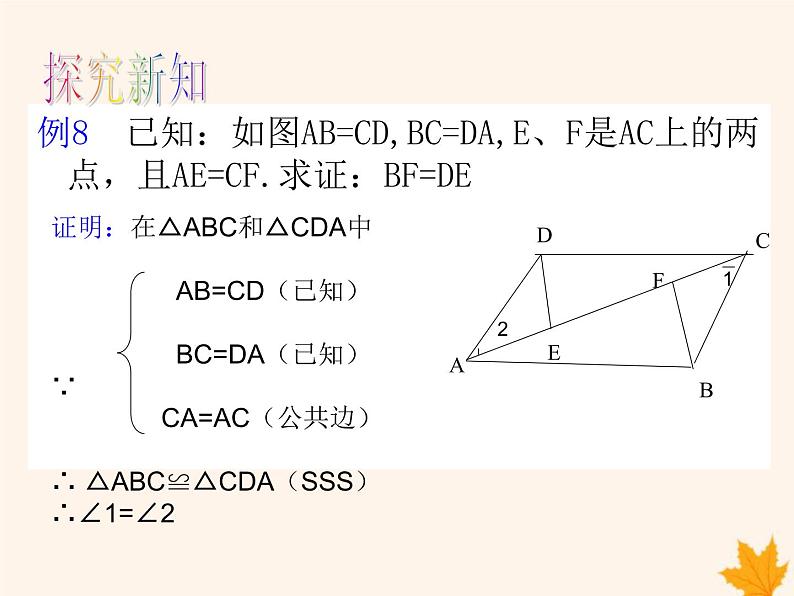
例8 已知：如图AB=CD,BC=DA,E、F是AC上的两点，且AE=CF.求证：BF=DE
证明：在△ABC和△CDA中 AB=CD（已知） BC=DA（已知）∵ CA=AC（公共边）∴ △ABC≌△CDA（SSS）∴∠1=∠2
在△BCF与△DAE中∵
BC=DA ( 已知 ）
∠1=∠2( 已证 )
∴△BCF≌△DAE(SAS)
∴BF=DE ( 全等三角形的对应边相等)
例9 证明：全等三角形对应边上的高相等。已知：△ABC≌△A′B′C′.AD,A′D′分别是△ABC和△A′B′C′的高.求证： AD=A′D′
证明：∵ ≌ （ ） ∴ = ， = （ ） 又∵ ， ∴ = =90°（ ）在△ 和△ 中∵∴ ≌ （AAS)∴ AD=A′D′( )
本节课你学习了哪些知识？
1.如图，已知：△ABC中，∠C=2∠B，AD平分∠BAC交BC于D.  求证：AB=AC+DC.
2.已知：△ABC中∠BAC=∠BCA，AD是△ABC的中线，延长BC到F,使CF=AB. 求证：AF=2AD.
3.如图，四边形ABCD的对角线AC、BD相交于点O，△ABC≌△BAD。求证：（1）OA=OB；（2）AB∥CD