四年级思维专项训练6 加法原理(试卷+解析)

四年级思维训练6 加法原理

1、波特有6只狗，如果他每次遛2只狗，那么狗的搭配情况总共             种

2、某地区有66条航空线路，每两个城市之间都设有一条直达的航空线，这66条航空线共

连接这个地区      个城市。

3、从1，2，3，4，5，6，7，8，9九个数中取3个数组成一组，使它的平均数是5，有     种           

取法．

4、有若干黑色和白色的圆形石头．将其中的7个如下图所示那样排列，请问：可以有多少种使黑石不相邻的排列方法？（注意：旋转后可重合的两种排列只算为一种．）

5、A.B.C三个小朋友互相传球，先从A开始发球（作为第一次传球），这样经过了5次传

球后，球恰巧又回到A手中，那么不同的传球方式共多少种？

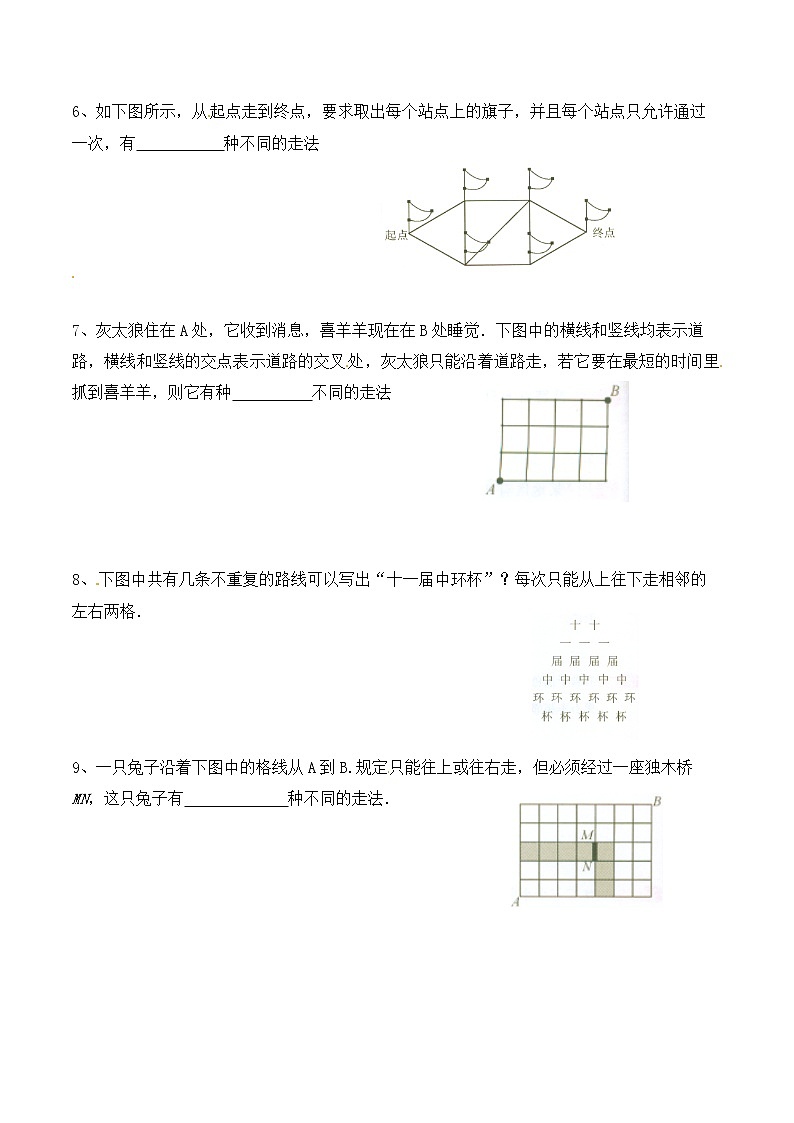
6、如下图所示，从起点走到终点，要求取出每个站点上的旗子，并且每个站点只允许通过

一次，有           种不同的走法

7、灰太狼住在A处，它收到消息，喜羊羊现在在B处睡觉．下图中的横线和竖线均表示道

路，横线和竖线的交点表示道路的交叉处，灰太狼只能沿着道路走，若它要在最短的时间里抓到喜羊羊，则它有种          不同的走法

8、下图中共有几条不重复的路线可以写出“十一届中环杯”？每次只能从上往下走相邻的

左右两格．

9、一只兔子沿着下图中的格线从A到B.规定只能往上或往右走，但必须经过一座独木桥

MN，这只兔子有             种不同的走法．

10、下图中有10个编好号码的房间，你可以从小号码房间走到相邻的大号码房问，但不能

从大号码走到小号码，从1号房间走到10号房间共有            种不同的走法．

11、在下图中，要从A走到B，不能经过C、D两点，如果只能向右、向上或斜上方走，一共有                种不同的走法．

12、池塘中10片莲叶如下图排列．青蛙在莲叶间跳跃，每次只能从一片莲叶跳到相邻的另

片莲叶，一只青蛙盘算着从其中一片莲叶上起跳，连跳4次，那么它有        种不同的跳法．

13、如下图所示，有一个4×8的棋盘，现将一枚棋子放在棋盘左下角格子A处，要求每一步只能向棋盘右上或右下走一步（如从C走一步可走到D或E），那么将棋子从A走到棋

盘右上角B处共有           种不同的走法．

14、下图是5×5的方格纸，小方格为边长1厘米的正方形，图中共有个正方形，

所有这些正方形的面积之和为           

15、如果一个大于9的整数，其每个数位上的数字都比它右边数位上的数字小，那么我们称

它为“迎春数”，那么，小于2008的“迎春数”共有          个

16、一些白瓷砖和黑瓷砖排成3×3的正方形．其中不含有两块相邻的黑瓷砖的拼法有    种．

（下图是其中的一种）

注意：

黑瓷砖一块都不使用，也算一种；

旋转后和原来重合的，算同一种；

只是翻转后和原来重合的，不算同一种，

四年级思维训练6 加法原理

参考答案

1、波特有6只狗，如果他每次遛2只狗，那么狗的搭配情况总共种      

【答案】1 5

【分析】我们给波特的6只狗分别编号为1、2、3、4、5、6，和编号1搭配的有12、13、14、15、16五种；和编号2搭配的有23.24、25.26四种；和编号3搭配的有34、35、36，3种；和编号4搭配的有45、46两种；和编号5搭配的有56 一种．因此共有5+4+3+2+1+1=15（种）

2、某地区有66条航空线路，每两个城市之间都设有一条直达的航空线，这66条航空线共

连接这个地区        个城市。

【答案】1 2

【分析】我们把各个城市看做线段的端点，两点间的线段代表两个城市间的航线，本题相当

于告诉了线段条数，求端点个数，因为1+2+1+3+……+11=66，所以相当于有12个端点，也就是有12个城市，

3、从1，2，3，4，5，6，7，8，9九个数中取3个数组成一组，使它的平均数是5，有       

取法．

【答案】8

【分析】三个数的平均数是5，也就是三个数的和为1 5，这3个数从最小的考虑：最小数为1的有(1，5，9)、(1，6，8)两种；最小数为2的有(2，4，9)、(2，5，8)、(2，6，7)三种；最小数为3的有(3，4，8)、(3，5，7)两种；最小数为4的有(4，5，6)-种，最小数为5，6，7，8，9的没有，因此一共有2+3+2+1=8（种）取法．

4、有若干黑色和白色的圆形石头．将其中的7个如下图所示那样排列，请问：可以有多少种使黑石不相邻的排列方法？（注意：旋转后可重合的两种排列只算为一种．）

【答案】6   

【分析】没有黑石时，有1种；只有一块黑石时，有2种；有两块时，有2种；有3块时，有1种，共1+2+2+1=6（种）

5、A.B.C三个小朋友互相传球，先从A开始发球（作为第一次传球），这样经过了5次传

球后，球恰巧又回到A手中，那么不同的传球方式共多少种？

【答案】10

【分析】如图，A第一次传给B，到第五次传回A有5种不同方式。同理，A第一次传给C，到第五次传回A也有5种不同方式，所以，根据加法原理，不同的传球方式共有5 +5=10（种）

6、如下图所示，从起点走到终点，要求取出每个站点上的旗子，并且每个站点只允许通过

一次，有           种不同的走法

【答案】4

【分析】给这些点依次标点（如下左图），然后采用枚举法（如下右图）

7、灰太狼住在A处，它收到消息，喜羊羊现在在B处睡觉．下图中的横线和竖线均表示道路，横线和竖线的交点表示道路的交叉处，灰太狼只能沿着道路走，若它要在最短的时间里抓到喜羊羊，则它有          种不同的走法

【答案】35

【分析】标数法．如右图所示

8、下图中共有几条不重复的路线可以写出“十一届中环杯”？每次只能从上往下走相邻的

左右两格．

【答案】62种

【分析】利用标数法，如下图所示，最后一共有6+15+20+15+6=62（种）路线可以写出“十一届中环杯”．

9、一只兔子沿着下图中的格线从A到B.规定只能往上或往右走，但必须经过一座独木桥MN，这只兔子有              种不同的走法．

【答案】150

【分析】标数法，如果桥的左上方和右下方的路线可以走的话，那么这只兔子必须向下或向左走，不合题意，因此只能标零，如下图所示，因此共有1 50种走法

10、下图中有10个编好号码的房间，你可以从小号码房间走到相邻的大号码房问，但不能

从大号码走到小号码，从l号房间走到10号房间共有          种不同的走法．

【答案】22

【分析】把这个图展开（见下图），用箭头标出行走方向，然后采用标数法即可

11、在下图中，要从A走到B，不能经过C、D两点，如果只能向右、向上或斜上方走，一共有                  种不同的走法．

【答案】17

【分析】利用标数法（见下图），每一点的走法数等于它的左方和下方两个点的方法数的和，

12、池塘中10片莲叶如下图排列．青蛙在莲叶间跳跃，每次只能从一片莲叶跳到相邻的另

片莲叶，一只青蛙盘算着从其中一片莲叶上起跳，连跳4次，那么它有          种不同的跳法．

【答案】2304

【分析】找规律．如下图所示，图1 ffI每点所标的数代表跳l步到达这个点的跳法总数，所以跳1步的方法数共2+4+4+4+6+4+2+4+4+2=36（种）；图2 中每点所标的数代表跳2步到达这个点的跳法总数（由图1中与此点相邻点上所标数相加而得），共8+16+16 +16+24+16+8+16+16+8=144（种）；不难发现对于每一点，多跳一步跳法就增加为原来的4倍，所以方法总数也增加为原来的4倍，因此跳3步有144×4=576（种），跳4步有576×4=2304（种）

13、如下图所示，有一个4×8的棋盘，现将一枚棋子放在棋盘左下角格子A处，要求每一步只能向棋盘右上或右下走一步（如从C走一步可走到D或E），那么将棋子从A走到棋

盘右上角B处共有           种不同的走法．

【答案】8

【分析】如下图所示，从A出发只能走到有阴影的格子中，由标数法可得，共有8种走法．

14、下图是5×5的方格纸，小方格为边长1厘米的正方形，图中共有个正方形，所有这些正方形的面积之和为        

【答案】55，259

【分析】图中面积为l、4、9、16、25平方厘米的正方形分别有5×5、4×4、3×3、2×2、1×1个，共有55个小正方形，所有正方形的面积和为25×1+16×4+9×9+4×16+1×25=259（平方厘米）

15、如果一个大于9的整数，其每个数位上的数字都比它右边数位上的数字小，那么我们称它为“迎春数”，那么，小于2008的“迎春数”共有           个

【答案】176

【分析】方法一：枚举法  ——按位数分类计算．

两位数中，“迎春数”个数

(1)十位数字是1，这样的“迎春数”有12，13，…，19，共8个；

(2)十位数字是2，这样的“迎春数”有23，…29，共7个

(3)十位数字是3，这样的“迎春数”有34，…39，共6个

(4)十位数字是4，这样的“迎春数”有45，…49，共5个

(5)十位数字是5，这样的“迎春数”有56，…59，共4个

(6)十位数字是6，这样的“迎春数”有67，68，69共3个

(7)十位数字是7，这样的“迎春数”有78，79，共2个；

(8)十位数字是8，这样的“迎春数”只有89这1个；

(9)没有十位数字是9的两位的“迎春数”；

所以两位数中，“迎春数”共有8+7+6+…+1=36（个）．

三位数中，“迎春数”个数

(1)百位数字是1，这样的“迎春数”有1123～29，134～139，…，189，共28个；

(2)百位数字是2，这样的“迎春数”有234~239，……289，共21个

(3)百位数字是3，这样的“迎春数”有345～349，……389，共15个

(4)百位数字是4，这样的“迎春数”有456～459，……489，共10个

(5)百位数字是5，这样的“迎春数”有567～569，…589，共6个

(6)百位数字是6，这样的“迎春数”有678，679，689，共3个

(7)百位数字是7，这样的“迎春数”只有789，这1个；

(8)没有百位数字是8，9的三位的“迎春数”；

所以三位数中，“迎春数”共有28+21 +15+10+6+3+1=84（个）

1000—1999的自然数中，“迎春数”个数

(1)前两位数字是12，这样的“迎春数”有12134～1239，…，1289，共21个

(2)前两位数字是13，这样的“迎春数”有1345～1349，…，1389，共15个

(3)前两位数字是14，这样的“迎春数”有1456~1459，…，1489，共10个

(4)前两位数字是15，这样的“迎春数”有1567～1569，…，1589，共6个

(5)前两位数字是1 6，这样的“迎春数”有1678，1 679，1 689共3个

(6)前两位数字是17，这样的“迎春数”只有1789这1个；

(7)没有前两位数字是18，19的四位的“迎春数”；

所以四位数中，“迎春数”共有56个．

2000～2008的白然数中，没有“迎春数”

所以小于2008的自然数巾，“迎春数”共有36 +84+56=176（个）．

 方法二：利用组合原理

    小于2008的“迎春数”，只可能是两位数、三位数和1000多的数．

    计算两位“迎春数”的个数，它就等于从1~9这9个数字中任意取 2个不同的数字，

    每一种取法对应于一个“迎春数”，即有多少种取法就有多少个“迎春数”．显然不同的取法有=9×8÷2=36（种），所以两位的“迎春数”共有36个．

    同样计算三位数和1000多的数数中“迎春数”的个数，它们分别有=9×8×7÷(3×2×1)=84（个）和=8×7×6÷(3×2×1)=56（个）．

 所以小于2008的白然数lf1，“迎春数”共有36+84+56=176（个）．

16、一些白瓷砖和黑瓷砖排成3×3的正方形．其中不含有两块相邻的黑瓷砖的拼法有    种．

（下图是其中的一种）

注意：

黑瓷砖一块都不使用，也算一种；

旋转后和原来重合的，算同一种；

只是翻转后和原来重合的，不算同一种，

【答案】21

【分析】如下图所示，按照对称位置把正方形的方格分类

┏━━┳━━┳━━┓

┃△  ┃O   ┃△  ┃

┣━━╋━━╋━━┫

┃O   ┃☆  ┃O   ┃

┣━━╋━━╋━━┫

┃△  ┃O   ┃△  ┃

┗━━┻━━┻━━┛

为避免重复，可固定一种位置来考虑，根据含有O的格中黑瓷砖的数目，分情况讨论

有1块的情况

如下图所示，把“不能放黑瓷砖的方格”用×表示（下同），则剩余2个方格中黑白瓷砖都可以放，共有2×2=4（种）方法，这4种方法互不相同，所以有4种

有2块的情况

如下图所示，黑瓷砖的位置有2种可能，

①如果两块黑瓷砖有公共顶点，则剩下的1个方格黑白瓷砖都可以放，有2种；

②如图所示，只有1种．

因此有2块的情况，共3种，

有3块的情况，如下图所示，只有1种

有4块的情况，如下图所示，只有1种

有0块的情况，如下图所示再按含△的方块中黑瓷砖数目分情况讨论：

0块：1种，1块：1中，2块：2种，3块：1种，4块：1种，共6种

又正中间的方格黑白瓷砖都可以放，所以，共有6×2 =12（种）．

综上所述，共有4+3+1+1+12= 21（种）．

点评：本题也可以先考虑含有△的方格，得出的结果是一样的，读者不妨尝试一下