




人教A版 (2019)必修 第一册3.2 函数的基本性质图文课件ppt
展开学习目标1.知识与能力目标 (1)理解偶函数、奇函数的定义。(2)能用定义来判断函数的奇偶性。 (3)掌握奇、偶函数图象的性质。 2.过程与方法目标 (1)初步培养学生数形结合的思想。 (2)从数和形两个角度理解函数的奇偶性。 3.情感态度与价值观目标 (1)体会具有奇偶性函数的图象对称的性质,感受数学的对称美,体现数学美学价值。 (2)通过函数奇偶性概念的形成过程,培养学生的观察、归纳、抽象的能力,同时渗透数形结合思想,从特殊到一般的数学思想。
在日常生活中,我们可以观察到许多对称现象,如:美丽的蝴蝶,盛开的花朵,以及建筑物和它在水中的倒影
一.现实生活中“美”的事例
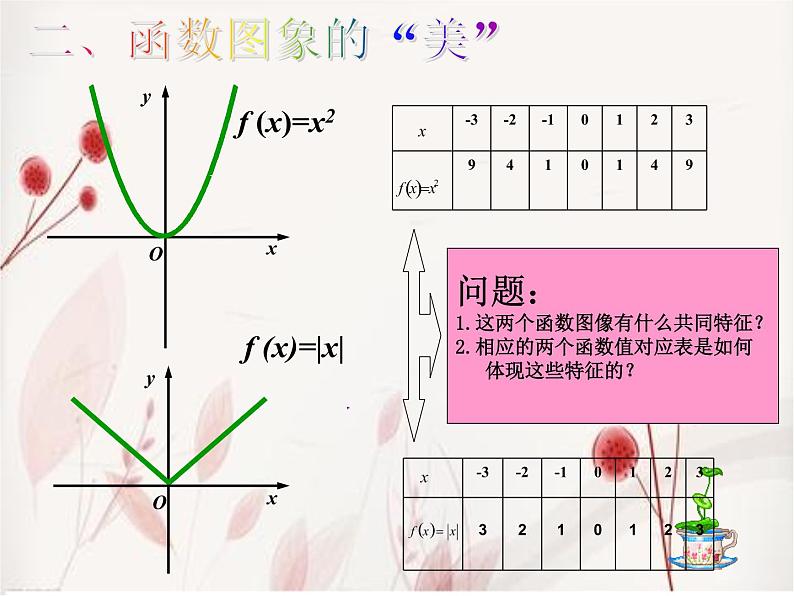
问题:1.这两个函数图像有什么共同特征?2.相应的两个函数值对应表是如何 体现这些特征的?
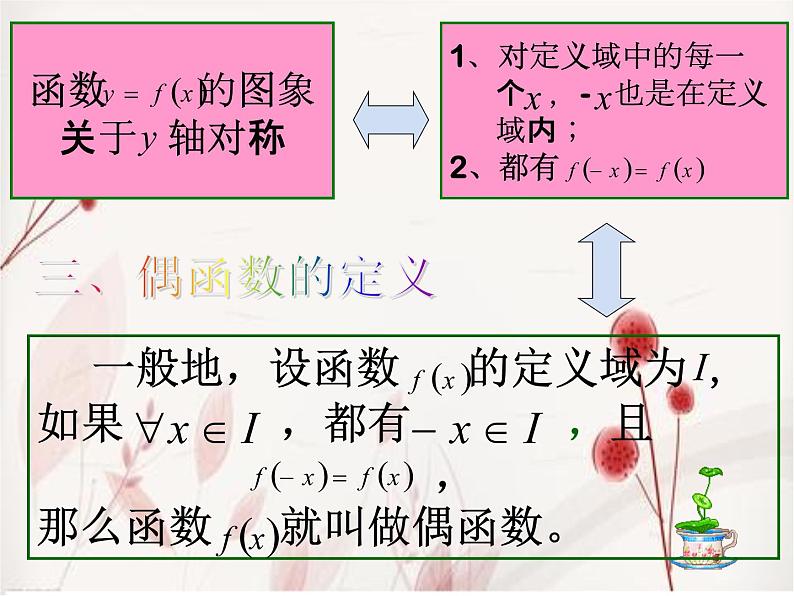
函数 的图象关于 轴对称
1、对定义域中的每一 个 ,- 也是在定义 域内;2、都有
一般地,设函数 的定义域为 ,如果 ,都有 ,且 ,那么函数 就叫做偶函数。
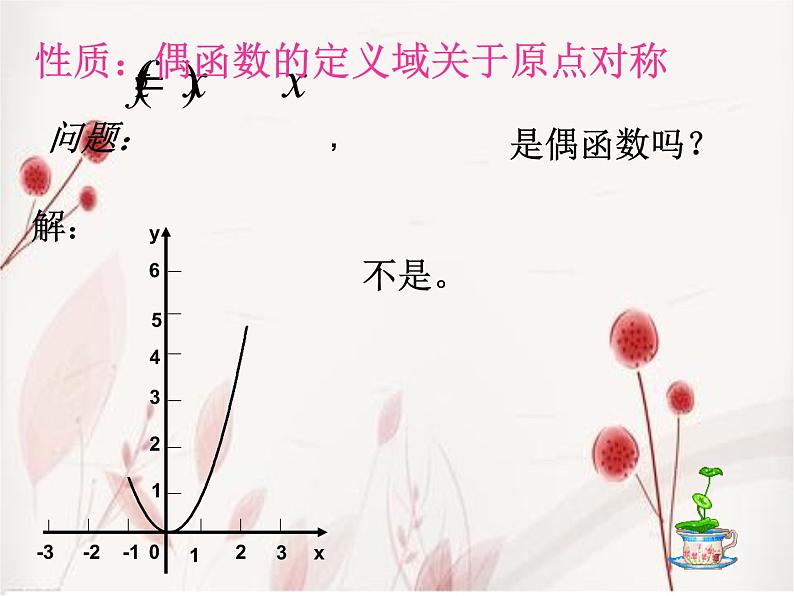
性质:偶函数的定义域关于原点对称
2、说说下面的函数是否为偶函数?
观察下面两个函数填写表格
问题:1.这两个函数图像有什么共同特征?2.相应的两个函数值对应表是如何体现这些特征的?
一般地,设函数 的定义域为 ,如果 ,都有 ,且 ,那么函数 就叫做奇函数。
函数 的图象关于原点成中心对称
性质:奇函数的定义域关于原点对称。
2、说说下面的函数是否为奇函数?
判定函数奇偶性基本方法: ①定义法: 先看定义域是否关于原点对称, 再看 与 的关系. ②图象法: 看图象是否关于原点或 轴对称.
七、如果一个函数 是奇函数或偶函数,那么我们就说函数 具有奇偶性.
定义域关于原点对称是判断函数具有奇偶性的先决条件
思考1:函数 是奇函数吗?是偶函数吗?
分析:函数的定义域为 但是 且∴ 既不是奇函数也不是偶函数。(也称为非奇非偶函数) 如右图所示:图像既不关于原点对称也不关于 轴对称。
奇函数 偶函数 函数可划分为四类: 既奇又偶函数 非奇非偶函数
说明: 1、根据函数的奇偶性
2、奇、偶函数性质: 偶函数的 定义域关于原点对称 图象关于 轴对称 奇函数的 定义域关于原点对称 图象关于原点对称。
例1.根据下列函数图象,判断函数奇偶性.
例2:判断下列函数的奇偶性:
变式练习:判断下列函数的奇偶性:
例3、已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.
变式训练:已知函数y=f(x)是奇函数,它右边的图象如下图,试将它补充完整.
2.若奇函数f(x)在[1,3]上为增函数,且有最小值0,则它在[-3,-1]上( )A.是减函数,有最小值0 B.是增函数,有最小值0C.是减函数,有最大值0 D.是增函数,有最大值0
奇偶性定义定义域关于原点对称是函数具有奇偶性的必 要条件。性质: 奇函数的图象关于原点对称; 偶函数的图象关于y轴对称.判断奇偶性方法:图象法,定义法。利用奇偶性求函数解析式。
课后作业: 优化设计1-6
人教A版 (2019)必修 第一册3.2 函数的基本性质教学演示课件ppt: 这是一份人教A版 (2019)必修 第一册3.2 函数的基本性质教学演示课件ppt,共30页。
人教A版 (2019)必修 第一册3.2 函数的基本性质教课课件ppt: 这是一份人教A版 (2019)必修 第一册3.2 函数的基本性质教课课件ppt,共17页。PPT课件主要包含了复习回顾,xx-1,题型二奇偶性的应用,方法小结等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质图片ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质图片ppt课件,共25页。PPT课件主要包含了f-3f3,f-2f2,f-1f1,g-3g3,g-2g2,g-1g1,定义域关于原点对称,1fxx4,2fxx5,方法总结等内容,欢迎下载使用。













