

苏教版 (2019)必修 第一册第6章 幂函数、指数函数和对数函数本章综合与测试优秀同步训练题
展开课时分层作业(三十一) 任意角的三角函数
(建议用时:40分钟)
一、选择题
1.已知点P(tan α,cs α)在第三象限,则角α的终边所在象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B [由P(tan α,cs α)在第三象限可知tan α<0,cs α<0.
由tan α<0得,角α的终边在第二或第四象限,
由cs α<0得,角α的终边在第二或第三象限或x轴的负半轴.
故角α的终边在第二象限.]
2.若角α的终边落在y=-x上,则tan α的值为( )
A.-1 B.1
C.-1或1 D.不能确定
A [设P(a,-a)是角α上任意一点,
若a>0,P点在第四象限,tan α=eq \f(-a,a)=-1,
若a<0,P点在第二象限,tan α=eq \f(-a,a)=-1.]
3.已知cs α>cs β,那么下列结论成立的是( )
A.若α,β是第一象限角,则sin α>sin β
B.若α,β是第二象限角,则tan α>tan β
C.若α,β是第三象限角,则sin α>sin β
D.若α,β是第四象限角,则tan α>tan β
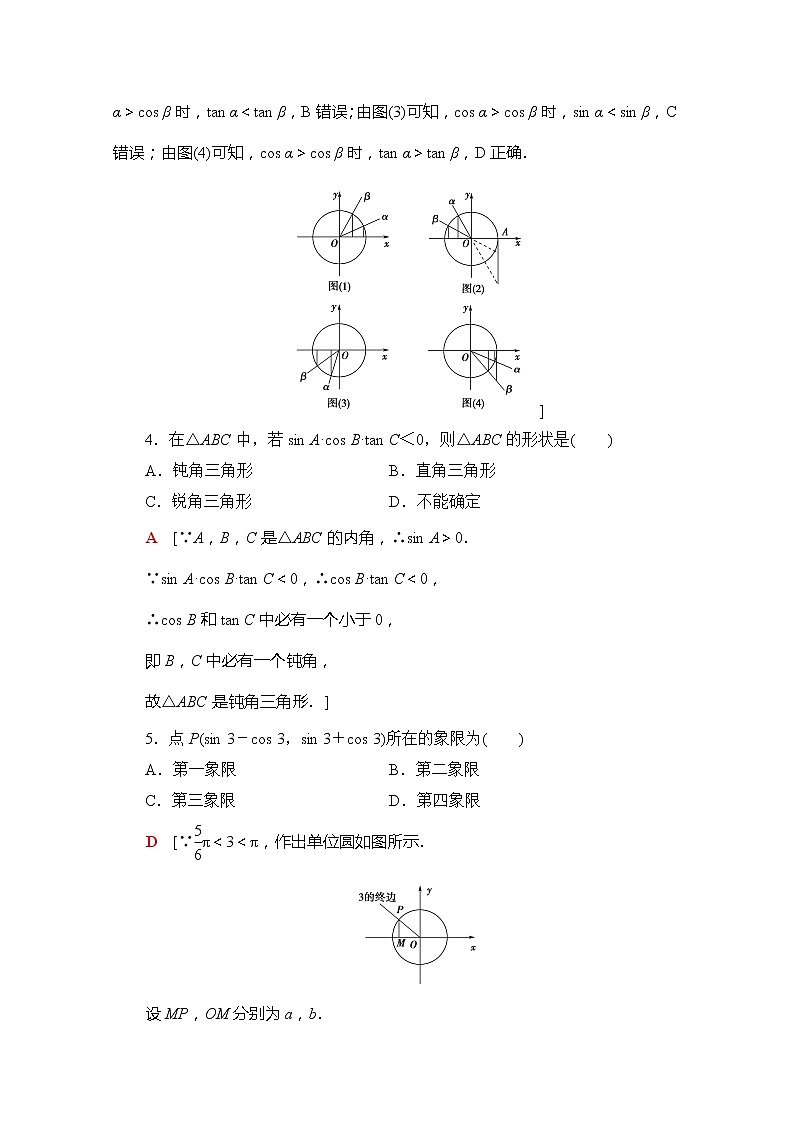
D [由图(1)可知,cs α>cs β时,sin α<sin β,A错误;由图(2)可知,cs α>cs β时,tan α<tan β,B错误;由图(3)可知,cs α>cs β时,sin α<sin β,C错误;由图(4)可知,cs α>cs β时,tan α>tan β,D正确.
]
4.在△ABC中,若sin A·cs B·tan C<0,则△ABC的形状是( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.不能确定
A [∵A,B,C是△ABC的内角,∴sin A>0.
∵sin A·cs B·tan C<0,∴cs B·tan C<0,
∴cs B和tan C中必有一个小于0,
即B,C中必有一个钝角,
故△ABC是钝角三角形.]
5.点P(sin 3-cs 3,sin 3+cs 3)所在的象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D [∵eq \f(5,6)π<3<π,作出单位圆如图所示.
设MP,OM分别为a,b.
sin 3=a>0,cs 3=b<0,
所以sin 3-cs 3>0.
因为|MP|<|OM|,即|a|<|b|,
所以sin 3+cs 3=a+b<0.
故点P(sin 3-cs 3,sin 3+cs 3)在第四象限.]
二、填空题
6.已知角α为第二象限角,则eq \r(sin α-cs α2)化简的结果为 .
sin α-cs α [因为角α为第二象限角,故sin α>0,cs α<0,因此eq \r(sin α-cs α2)=|sin α-cs α|=sin α-cs α.]
7.sin eq \f(2π,5),cs eq \f(6π,5),tan eq \f(2π,5)按从小到大的顺序排列是 .
cs eq \f(6π,5)
cs eq \f(6π,5)<0,tan eq \f(2π,5)>0,
sin eq \f(2π,5)>0.
∵MP
故cs eq \f(6π,5)
8.已知角α的终边经过点(3a-9,a+2),且sin α>0,cs α≤0,则a的取值范围是 .
(-2,3] [因为cs α≤0,sin α>0,所以角α的终边在第二象限或y轴非负半轴上.
因为α的终边过点(3a-9,a+2),
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(3a-9≤0,,a+2>0,))所以-2<a≤3.]
三、解答题
9.判断下列各式的符号:
(1)sin 340°cs 265°;
(2)eq \f(sincs θ,cssin θ)(θ为第二象限角).
[解] (1)∵340°是第四象限角,265°是第三象限角,
∴sin 340°<0,cs 265°<0,
∴sin 340°cs 265°>0.
(2)∵θ为第二象限角,
∴0<sin θ<1<eq \f(π,2),-eq \f(π,2)<-1<cs θ<0,
∴sin(cs θ)<0,cs(sin θ)>0,∴eq \f(sincs θ,cssin θ)<0.
10.已知eq \f(1,|sin α|)=-eq \f(1,sin α),且lg cs α有意义.
(1)试判断角α所在的象限;
(2)若角α的终边上一点Meq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,5),m)),且|OM|=1(O为坐标原点),求m的值及sin α的值.
[解] (1)由eq \f(1,|sin α|)=-eq \f(1,sin α)可知sin α<0,
∴α是第三或第四象限角或终边在y轴的负半轴上的角.
由lg cs α有意义可知cs α>0,
∴α是第一或第四象限角或终边在x轴的非负半轴上的角.
综上可知角α是第四象限的角.
(2)∵|OM|=1,∴eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,5)))eq \s\up12(2)+m2=1,解得m=±eq \f(4,5).
又α是第四象限角,故m<0,从而m=-eq \f(4,5).
由正弦函数的定义可知sin α=eq \f(y,r)=eq \f(m,|OM|)=eq \f(-\f(4,5),1)=-eq \f(4,5).
1.已知点Peq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2),-\f(1,2)))在角θ的终边上,且θ∈[0,2π),则θ的值为( )
A.eq \f(5π,6) B.eq \f(2π,3)
C.eq \f(11π,6) D.eq \f(5π,3)
C [因为点Peq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2),-\f(1,2)))在第四象限,所以根据三角函数的定义可知tan θ=eq \f(-\f(1,2),\f(\r(3),2))=-eq \f(\r(3),3),
又θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2),2π)),所以θ=eq \f(11π,6).]
2.若α为第四象限角,则下列函数值一定是负值的是( )
A.sin eq \f(α,2) B.cs eq \f(α,2)
C.tan eq \f(α,2) D.cs 2α
C [由α为第四象限角,得2kπ+eq \f(3π,2)<α<2kπ+2π(k∈Z),故kπ+eq \f(3π,4)<eq \f(α,2)<kπ+π(k∈Z).
当k=2n(n∈Z)时,eq \f(α,2)∈eq \b\lc\(\rc\)(\a\vs4\al\c1(2nπ+\f(3π,4),2nπ+π)),
此时,eq \f(α,2)是第二象限角;
当k=2n+1(n∈Z)时,eq \f(α,2)∈eq \b\lc\(\rc\)(\a\vs4\al\c1(2nπ+\f(7π,4),2nπ+2π)),此时,eq \f(α,2)是第四象限角.
故无论eq \f(α,2)终边落在第二还是第四象限,tan eq \f(α,2)<0恒成立.
又4kπ+3π<2α<4kπ+4π(k∈Z).
故cs 2α有可能为正也有可能为负.]
3.如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为eq \f(4,5),则cs α= .
-eq \f(3,5) [因为点A纵坐标yA=eq \f(4,5),且A点在第二象限,又因为圆O为单位圆,所以点A横坐标xA=-eq \f(3,5),由三角函数的定义可得cs α=-eq \f(3,5).]
4.若0<α<2π,且sin α
eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(π,3)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,3),2π)) [利用三角函数线得α的终边落在如图所示∠AOB区域内,所以α的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(π,3)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,3),2π)).]
5.已知直线y=x与圆x2+y2=1交于A,B两点, 点A在x轴的上方,O是坐标原点.
(1)求以射线OA为终边的角α的正弦值和余弦值;
(2)求以射线OB为终边的角β的正切值.
[解] (1)由eq \b\lc\{\rc\ (\a\vs4\al\c1(y=x,,x2+y2=1,))
得eq \b\lc\{\rc\ (\a\vs4\al\c1(x1=\f(\r(2),2),,y1=\f(\r(2),2)))或eq \b\lc\{\rc\ (\a\vs4\al\c1(x2=-\f(\r(2),2),,y2=-\f(\r(2),2).))
∵点A在x轴上方,
∴点A,B的坐标分别为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2),\f(\r(2),2))),eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(\r(2),2),-\f(\r(2),2))).
∴sin α=eq \f(\r(2),2),cs α=eq \f(\r(2),2).
(2)由(1)得tan β=eq \f(-\f(\r(2),2),-\f(\r(2),2))=1.
数学必修 第一册第5章 函数概念与性质本章综合与测试精品课后作业题: 这是一份数学必修 第一册第5章 函数概念与性质本章综合与测试精品课后作业题,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高中数学苏教版 (2019)必修 第一册第1章 集合本章综合与测试精品课后练习题: 这是一份高中数学苏教版 (2019)必修 第一册第1章 集合本章综合与测试精品课后练习题,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高中数学苏教版 (2019)必修 第一册第1章 集合本章综合与测试精品复习练习题: 这是一份高中数学苏教版 (2019)必修 第一册第1章 集合本章综合与测试精品复习练习题,共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













