人教A版(2019)高一数学必修第二册--正弦定理、余弦定理应用举例-【课件】

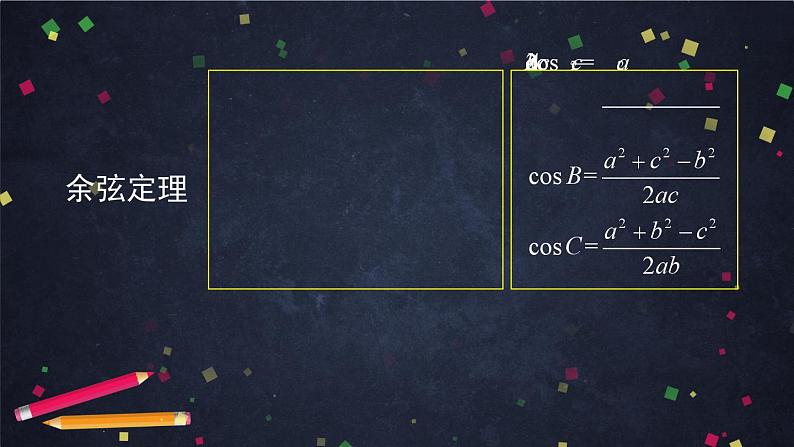
这是一份人教A版(2019)高一数学必修第二册--正弦定理、余弦定理应用举例-【课件】，共60页。PPT课件主要包含了余弦定理，正弦定理，测量工具，指北方向线，例题解析，由正弦定理，方向北偏东，所求三角形，△ABC，△ABD等内容，欢迎下载使用。
在水平方向上 我们称: 指北或指南方向线与目标方向线所成的小于90°的水平角, 叫方向角.
在水平方向上 我们称: 指北或指南方向线与目标方向线所成的小于90°的水平角, 叫方向角. 例如图中就是北偏西30°
在水平方向上 我们称: 指北或指南方向线与目标方向线所成的小于90°的水平角, 叫方向角. 例如图中就是北偏西30°和北偏东45°.
除此之外 对于竖直方向的夹角和水平方向的夹角, 经纬仪也可以进行测量.
例1. 某海域A处的灯塔甲获悉, 在其正东方向相距20海里的B处有一艘渔船遇险后抛锚等待救援. 灯塔甲立即把消息告知位于其南偏西30°相距7海里的C处的乙船. 那么, 乙船前往营救遇险渔船时需要航行的最小距离是多少海里(精确到1海里) ？航行目标方向线的方向是北偏东多少度(精确到1°)？
例1. 某海域A处的灯塔甲获悉, 在其正东方向相距20海里的B处有一艘渔船遇险后抛锚等待救援. 灯塔甲立即把消息告知位于其南偏西30°相距7海里的C处的乙船. 那么, 乙船前往营救遇险渔船时需要航行的最小距离是多少海里(精确到1海里) ？航行目标方向线的方向是北偏东多少度(精确到1°)？
例1. 某海域A处的灯塔甲获悉, 在其正东方向相距20海里的B处有一艘渔船遇险后抛锚等待救援. 灯塔甲立即把消息告知位于其南偏西30°相距7海里的C处的乙船.
所以 .
方向：北偏东距离：24海里.
例2. A, B两点都在河的对岸(不可到达), 设计一种测量A, B两点间距离的方法, 并求出A, B两点间的距离.
△ACD中,
△ACD中, .
△BCD中,
△BCD中, .
△ABC中, 余弦定理求AB
△ABD中, 余弦定理求AB
例3. 求旗杆AB的高度.
选定测量基点C. 测量仰角∠ACB的大小以及BC两点间距离.
选定测量基点C. 测量仰角∠ACB的大小以及BC两点间距离. 计算旗杆的高度
选定测量基点C. 测量仰角∠ACB的大小以及BC两点间距离. 计算旗杆的高度
例4. AB是底部点B不可到达的一座山, 点A为山的最高点, 点B为点A在水平面上的投影. 设计一种测量山高的方法, 并计算出山的高度.
例5. AB是底部点B不可到达的一座山, 点A为山的最高点, 点B为点A在水平面上的投影. 在一条笔直的公路CD上的C, D两点处测得A点仰角的大小分别是 和 , 若CD两点间距离为a, 设计一种测量山高的方法, 并计算出山的高度.
在△ABC中, .
在△ABD中, .
在△BCD中,
在△BCD中, .
在△BCD中, 由正弦定理 .
或 .
或者 .
作业1. 一艘船向正北航行, 航行速度的大小为32.2 n mile/h, 在A处看灯塔S在船的北偏东20°的方向上. 30min后, 船航行到B处, 在B处看灯塔在船的北偏东65°的方向上. 已知距离此灯塔6.5 n mile以外的海区为航行安全区域, 这艘船可以继续沿正北方向航行吗？