

11.山西省部分学校2023-2024学年高一上学期期末数学试题
展开
这是一份11.山西省部分学校2023-2024学年高一上学期期末数学试题,共11页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
一、单选题
1.已知集合,,则( )
A.B.C.D.
2.已知扇形的圆心角为,半径为4,则扇形的弧长为( )
A.B.2C.4D.8
3.不等式的解集为( )
A.B.C.D.
4.函数的零点所在区间为( )
A.B.C.D.
5.下列区间为函数的增区间的是( )
A.B.C.D.
6.已知,,则等于( )
A.B.C.D.
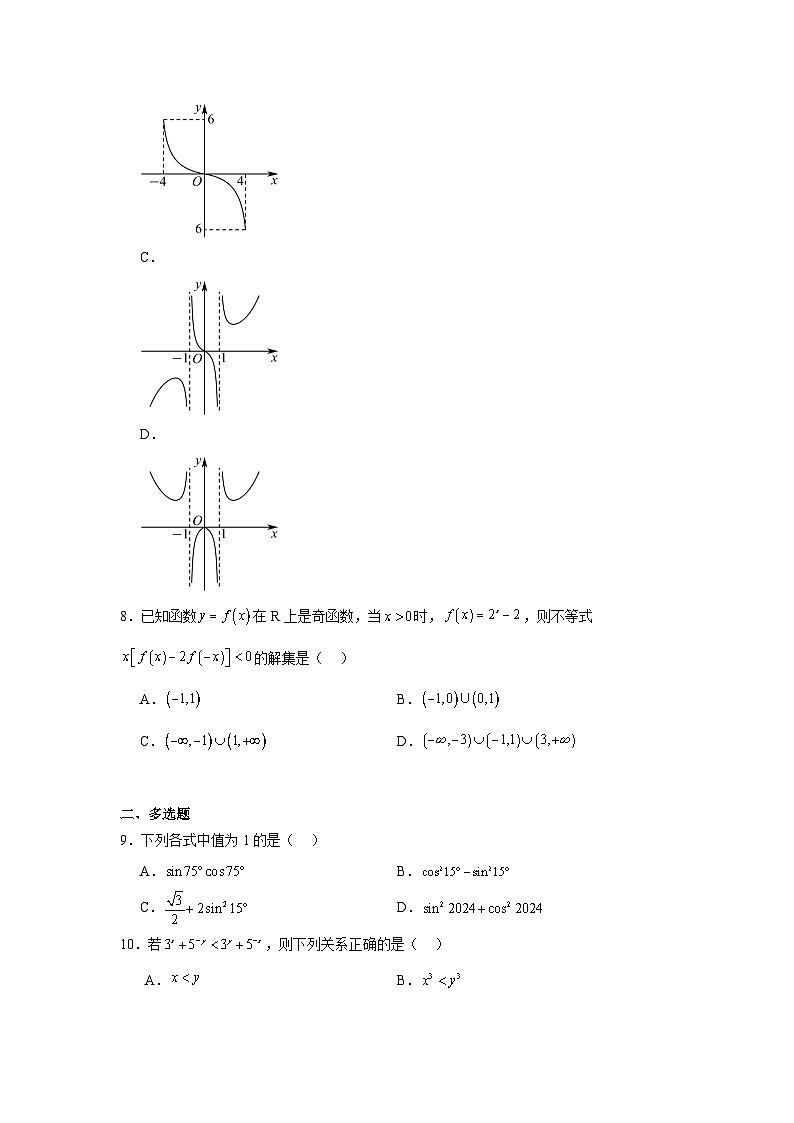
7.函数的图象大致是( )
A.
B.
C.
D.
8.已知函数在R上是奇函数,当时,,则不等式的解集是( )
A.B.
C.D.
二、多选题
9.下列各式中值为1的是( )
A.B.
C.D.
10.若,则下列关系正确的是( )
A.B.
C.D.
11.若,且,则下列不等式恒成立的是( )
A.B.
C.D.
12.已知函数,若,则( )
A.B.
C.D.在上无最值
三、填空题
13.若是定义域为的幂函数,则 .
14.函数的图象关于原点对称,则
15.已知函数,若存在且,使得,则的取值范围为 .
16.函数在区间上的最小值为 .
四、解答题
17.(1)已知为第二象限角,求的值;
(2)化简:.
18.已知集合.
(1)若,求;
(2)若是的必要条件,求实数的取值范围.
19.已知关于的不等式的解集为或.
(1)求,的值;
(2)当时,求关于的不等式的解集(用表示).
20.已知函数.
(1)若,且为奇函数,求的值;
(2)若,且的最小值为,求的最小值.
21.据国家气象局消息,今年各地均出现了极端高温天气.漫漫暑期,某制冷杯成了畅销商品.该制冷杯根据物体的降温遵循牛顿冷却定律,即如果某液体的初始温度为(单位:),那么经过分钟后,温度满足,其中为室温,为参数.为模拟观察制冷杯的降温效果,小明把一杯的茶水放在的房间,10分钟后茶水降温至.(参考数据:)
(1)若欲将这杯茶水继续降温至,大约还需要多少分钟?(保留整数)
(2)某企业生产制冷杯每月的成本(单位:万元)由两部分构成:①固定成本(与生产产品的数量无关):20万元;②生产所需材料成本:万元,(单位:万套)为每月生产产品的套数.
(i)该企业每月产量为何值时,平均每万套的成本最低?一万套的最低成本为多少?
(ii)若每月生产万套产品,每万套售价为:万元,假设每套产品都能够售出,则该企业应如何制定计划,才能确保该制冷杯每月的利润不低于520万元?
22.如图,已知函数的图象与轴相交于点,图象的一个最高点为.
(1)求的解析式;
(2)将函数的图象向左平移个单位长度,得到函数的图象,求函数的所有零点之和.
参考答案:
1.C
2.D
3.A
4.C
5.B
6.C
7.C
8.B
9.CD
10.ABD
11.AD
12.ABC
13.2
14.
15.
16.1
17.(1);(2)
【解析】
(1)为第二象限角,
,
所以.
(2)因为,
,,
所以原式.
18.(1)
(2)或
【解析】(1)解不等式可得,则,
若,则,
所以.
(2)若是的必要条件,则.
当,即时,,符合题意;
当,即时,,要满足,
可得,
解得,
综上实数的取值范围为或
19.(1)
(2)答案见解析
【解析】(1)因为关于的不等式的解集为或,
所以1,2是方程的两根,
所以,解得;
(2)由(1)知关于的不等式,即为,
令得或,
①时,不等式的解集为;
②时,解得,不等式的解集为;
③时,解得,不等式的解集为.
20.(1)
(2)4
【解析】(1)当时,,
因为是奇函数,所以,
即,得,可得.
(2)令,则,
所以,即,
当且仅当,即时等号成立,所以,
由题意,,所以.所以,
当且仅当时等号成立,由,解得,
所以的最小值为4
21.(1)8分钟
(2)(i)该企业每月产量20万套时,一万套的成本最低,一万套的最低成本为12万元;(ii)至少生产20万套产品
【解析】(1)由题意可得,解得,
设经过分钟,这杯茶水由降温至,则,
解得,
故欲将这杯茶水继续降温至,大约还需要8分钟.
(2)解:(i)设平均每一万套所需的成本费用为万元,
则有,
当且仅当,即时取等号,
所以该企业每月产量20万套时,一万套的成本最低,一万套的最低成本为12万元;
(ii)设月利润为万元,
则有,
解得(舍去)或,
所以该企业每月至少生产20万套产品,才能确保该制冷杯每月的利润不低于520万元.
22.(1)
(2)9
【解析】(1)设的最小正周期为,则,
所以,所以,
又因为函数的图象的一个最高点为,
所以,所以,
所以,
因为,所以,所以.
(2)将函数的图象向左平移个单位长度,得到函数的图象,
所以,
令,得,
考虑与图象的所有交点的横坐标之和,
函数与的图象都关于点对称,
令,解得,
函数与的图象如图所示:
故两函数的图象有且仅有9个交点从左到右分别为,
所以,,,,
所以,故函数的所有零点之和为9.
相关试卷
这是一份山西省部分学校2023-2024学年高一上学期期末数学试题,共11页。试卷主要包含了本试卷分选择题和非选择题两部分,本卷命题范围,下列区间为函数的增区间的是,已知,则,函数的图象大致是,下列各式中值为1的是,若,则下列关系正确的是等内容,欢迎下载使用。
这是一份重庆市部分学校2023-2024学年高一上学期期末联考数学试题,共4页。
这是一份2023-2024学年山西省部分学校高一上学期12月联合考试数学试题含答案,共13页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。









