滨州市重点中学2024年九上数学开学教学质量检测试题【含答案】

这是一份滨州市重点中学2024年九上数学开学教学质量检测试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，PA、PB分别与⊙O相切于点A、B，若∠P=50°，则∠C的值是（ ）
A．50°B．55°C．60°D．65°
2、（4分）如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为10,则该直线的函数表达式是( )
A．y=x+5B．y=x+10C．y=-x+5D．y=-x+10
3、（4分）某科普小组有5名成员，身高分别为（单位：cm）：160，165，170，163，1．增加1名身高为165cm的成员后，现科普小组成员的身高与原来相比，下列说法正确的是（ ）
A．平均数不变，方差不变B．平均数不变，方差变大
C．平均数不变，方差变小D．平均数变小，方差不变
4、（4分）下列二次根式中与是同类二次根式的是（ ）
A．B．C．D．
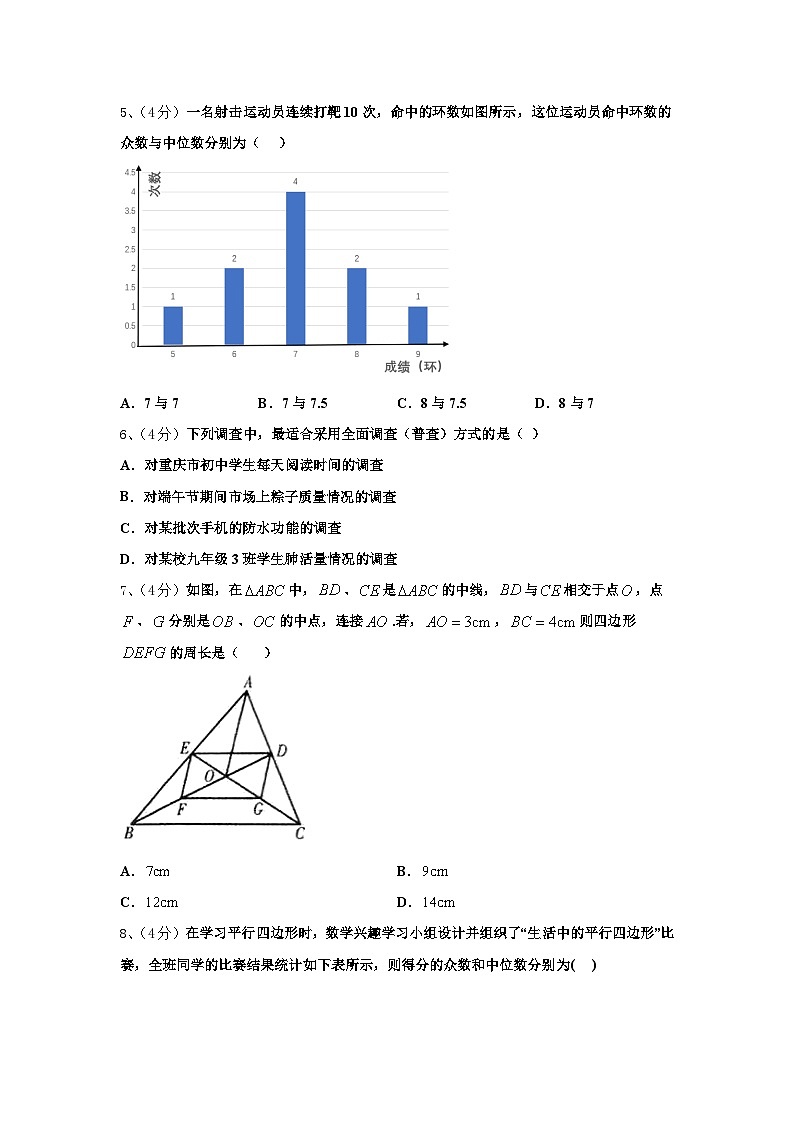
5、（4分）一名射击运动员连续打靶10次，命中的环数如图所示，这位运动员命中环数的众数与中位数分别为（ ）
A．7与7B．7与7.5C．8与7.5D．8与7
6、（4分）下列调查中，最适合采用全面调查（普查）方式的是（ ）
A．对重庆市初中学生每天阅读时间的调查
B．对端午节期间市场上粽子质量情况的调查
C．对某批次手机的防水功能的调查
D．对某校九年级3班学生肺活量情况的调查
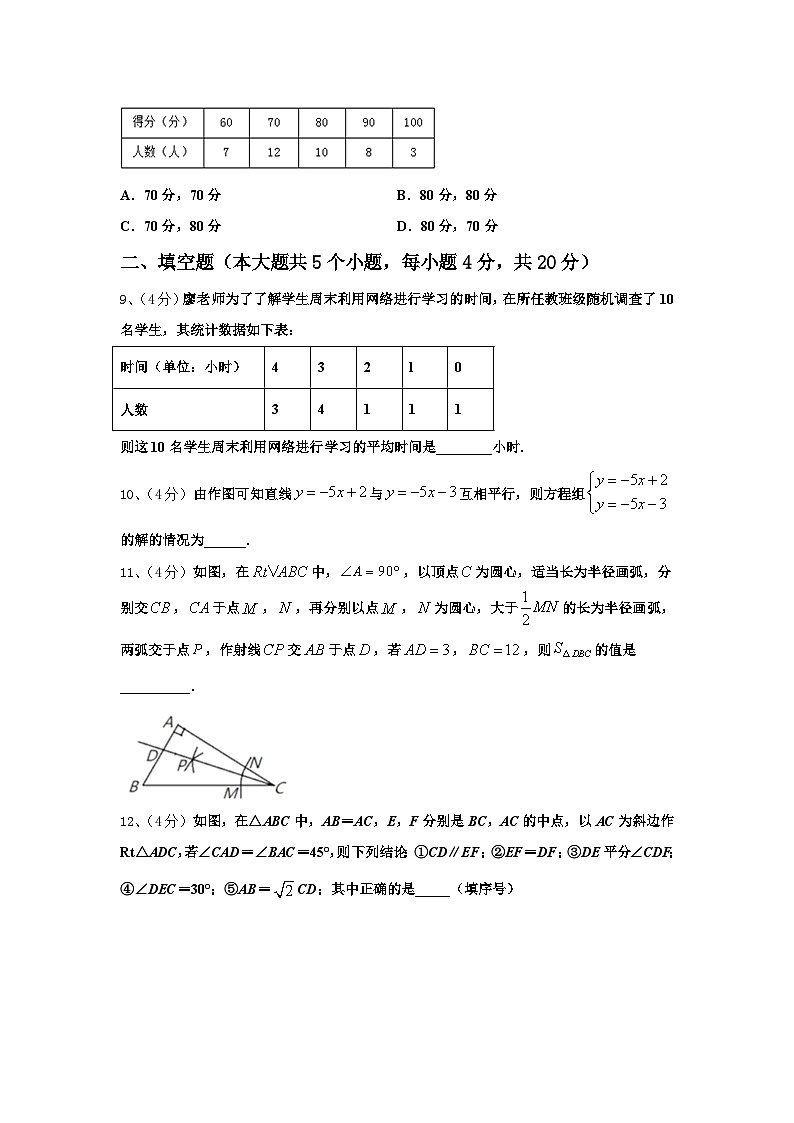
7、（4分）如图，在中，、是的中线，与相交于点，点、分别是、的中点，连接.若，，则四边形的周长是（ ）
A．B．
C．D．
8、（4分）在学习平行四边形时，数学兴趣学习小组设计并组织了“生活中的平行四边形”比赛，全班同学的比赛结果统计如下表所示，则得分的众数和中位数分别为( )
A．70分，70分B．80分，80分
C．70分，80分D．80分，70分
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）廖老师为了了解学生周末利用网络进行学习的时间，在所任教班级随机调查了10名学生，其统计数据如下表：
则这10名学生周末利用网络进行学习的平均时间是________小时.
10、（4分）由作图可知直线与互相平行，则方程组的解的情况为______.
11、（4分）如图，在中，，以顶点为圆心，适当长为半径画弧，分别交，于点，，再分别以点，为圆心，大于的长为半径画弧，两弧交于点，作射线交于点，若，，则的值是__________．
12、（4分）如图，在△ABC中，AB＝AC，E，F分别是BC，AC的中点，以AC为斜边作Rt△ADC，若∠CAD＝∠BAC＝45°，则下列结论：①CD∥EF；②EF＝DF；③DE平分∠CDF；④∠DEC＝30°；⑤AB＝CD；其中正确的是_____（填序号）
13、（4分） 分解因式：9a﹣a3＝_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）已知，在平面直角坐标系中，直线经过点和点.
（1）求直线所对应的函数表达式.
（2）若点在直线上，求的值.
15、（8分）解不式并把它的解集表示在数轴上.
16、（8分）小明家准备给边长为6m的正方形客厅用黑色和白色两种瓷砖铺设，如图所示：①黑色瓷砖区域Ⅰ：位于四个角的边长相同的小正方形及宽度相等的回字型边框（阴影部分），②白色瓷砖区域Ⅱ：四个全等的长方形及客厅中心的正方形（空白部分）．设四个角上的小正方形的边长为x（m）．
（1）当x=0.8时，若客厅中心的正方形瓷砖铺设的面积为16m2，求回字型黑色边框的宽度；
（2）若客厅中心的正方形边长为4m，白色瓷砖区域Ⅱ的总面积为26m2，求x的值．
17、（10分）如图，在四边形ABCD中，，E为BD中点，延长CD到点F，使．
求证：
求证：四边形ABDF为平行四边形
若，，，求四边形ABDF的面积
18、（10分）直线与抛物线交于、两点，其中在轴上，是抛物线的顶点．
（1）求与的函数解析式；
（2）求函数值时的取值范围．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）方程的根是_____．
20、（4分）在平面直角坐标系中，已知点A（﹣，0），B（，0），点C在x轴上，且AC+BC=6，写出满足条件的所有点C的坐标_____．
21、（4分）如图，菱形ABCD中，对角线AC，BD相交于点O，点E，F分别是的边AB，BC边的中点若，
，则线段EF的长为______．
22、（4分）在平行四边形ABCD中，∠B+∠D＝190°，则∠A＝_____°．
23、（4分）已知一次函数的图像经过点（2，3），则的值为 ▲
二、解答题（本大题共3个小题，共30分）
24、（8分）计算：×+÷﹣|﹣2|
25、（10分）如图，从电线杆离地面5m处向地面拉一条长13m的缆绳，这条缆绳在地面的固定点距离电线杆底部有多远？
26、（12分）在“6.26”国际禁毒日到来之际，为了普及禁毒知识，提高市民禁毒意识，某区发放了一批“关爱生命，拒绝毒品”的宣传资料．据统计，甲小区共收到宣传资料350份，乙小区共收到宣传资料100份，甲小区住户比乙小区住户的3倍多25户，若两小区每户平均收到资料的数量相同．求这两小区各有多少户住户？
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
连接OA、OB，由已知的PA、PB与圆O分别相切于点A、B，根据切线的性质得到OA⊥AP，OB⊥PB，从而得到∠OAP=∠OBP=90°，然后由已知的∠P的度数，根据四边形的内角和为360°，求出∠AOB的度数，最后根据同弧所对的圆周角等于它所对圆心角度数的一半即可得到∠C的度数．
【详解】
解：连接OA、OB，
∵PA、PB与圆O分别相切于点A、B，
∴OA⊥AP，OB⊥PB，
∴∠OAP=∠OBP=90°，又∠P=50°，
∴∠AOB=360°-90°-90°-50°=130°，
又∵∠ACB和∠AOB分别是弧AB所对的圆周角和圆心角，
∴∠C=∠AOB=×130°=65°．
故选：D．
此题考查了切线的性质，以及圆周角定理．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题，同时要求学生掌握同弧所对的圆周角等于所对圆心角的一半．
2、C
【解析】
设P点坐标为(x,y)，如图，过P点分别作PD⊥x轴，PC⊥y轴，垂足分别为D. C，
∵P点在第一象限，
∴PD=y，PC=x，
∵矩形PDOC的周长为10，
∴2(x+y)=10，
∴x+y=5，即y=−x+5，
故选C.
点睛:本题主要考查矩形的性质及点的坐标的意义,根据坐标的意义得出x,y之间的关系是解题的关键.
3、C
【解析】
解： =（160+165+170+163+1）÷5=165，S2原=， =（160+165+170+163+1+165）÷6=165，S2新=，平均数不变，方差变小，故选C．
4、B
【解析】
先将各选项化简,再根据同类二次根式的定义解答.
【详解】
A、,与被开方数不相同,故不是同类二次根式,选项错误;
B、,与被开方数相同,故是同类二次根式,选项正确;
C、,与被开方数不同,故不是同类二次根式,选项错误;
D、是整数,不是二次根式,故选项错误.
所以B选项是正确的.
本题主要考查同类二次根式的定义，正确对根式进行化简,以及正确理解同类二次根式的定义是解决问题的关键.
5、A
【解析】
根据众数的定义找出出现次数最多的数；根据中位数的定义求出最中间两个数的平均数即可．
【详解】
解：根据统计图可得：
7出现了4次，出现的次数最多，
则众数是7；
∵共有10个数，
∴中位数是第5和6个数的平均数，
∴中位数是（7+7）÷2=7；
故选：A．
此题考查了众数和中位数，用到的知识点是众数和中位数的定义，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），众数是一组数据中出现次数最多的数，注意众数不止一个．
6、D
【解析】
A、对重庆市初中学生每天阅读时间的调查，调查范围广适合抽样调查，故A错误；
B、对端午节期间市场上粽子质量情况的调查，调查具有破坏性，适合抽样调查，故B错误；
C、对某批次手机的防水功能的调查，调查具有破坏性，适合抽样调查，故C错误；
D、对某校九年级3班学生肺活量情况的调查，人数较少，适合普查，故D正确；
故选D．
7、A
【解析】
根据三角形的中位线即可求解.
【详解】
依题意可知D,E,F,G分别是AC,AB,BO,CO的中点，
∴DE是△ABC的中位线，FG是△OBC的中位线，EF是△ABO的中位线，DG是△AOC的中位线，
∴DE=FG=BC=2cm，EF=DG=AO=cm，
∴四边形的周长是DE+EF+FG+DG=7cm,
故选A.
此题主要考查中位线的性质，解题的关键是熟知三角形中位线的判定与性质.
8、C
【解析】
根据众数的定义，找到该组数据中出现次数最多的数即为众数；根据中位数定义，将该组数据按从小到大依次排列，处于中间位置的两个数的平均数即为中位数．
【详解】
解：∵70分的有12人，人数最多，
∴众数为70分；
处于中间位置的数为第20、21两个数，都为80分，中位数为80分．
故选：C．
本题为统计题，考查众数与中位数的意义，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、2.1
【解析】
依据加权平均数的概念求解可得．
【详解】
解：这10名学生周末利用网络进行学习的平均时间是：
；
故答案为：2.1．
本题主要考查加权平均数，解题的关键是掌握加权平均数的定义．
10、无解
【解析】
二元一次方程组的解，就是两个函数图象的交点坐标，当两函数图象平行时，两个函数无交点，因此解析式所组成的方程组无解．
【详解】
∵直线y=-5x+2与y=-5x-3互相平行，
∴方程组无解，
故答案为：无解．
此题主要考查了一次函数与二元一次方程组的关系，关键是掌握二元一次方程组的解，就是两个函数图象的交点．
11、1
【解析】
过点D作DE⊥BC于E，根据角平分线的作法可知CD平分∠ACB，然后根据角平分线的性质可得DE=AD=3，然后根据三角形的面积公式求面积即可．
【详解】
解：过点D作DE⊥BC于E
由题意可知：CD平分∠ACB
∵
∴DE=AD=3
∵
∴=
故答案为：1．
此题考查的是用尺规作图作角平分线和角平分线的性质，掌握角平分线的作法和角平分线的性质是解决此题的关键．
12、①②③⑤
【解析】
根据三角形中位线定理得到EF＝AB，EF∥AB，根据直角三角形的性质得到DF＝AC，根据三角形内角和定理、勾股定理计算即可判断．
【详解】
∵E，F分别是BC，AC的中点，
∴EF＝AB，EF∥AB，
∵∠ADC＝90°，∠CAD＝45°，
∴∠ACD＝45°，
∴∠BAC＝∠ACD，
∴AB∥CD，
∴EF∥CD，故①正确；
∵∠ADC＝90°，F是AC的中点，
∴DF＝CF=AC，
∵AB=AC，EF＝AB，
∴EF＝DF，故②正确；
∵∠CAD=∠ACD=45°，点F是AC中点，
∴△ACD是等腰直角三角形，DF⊥AC，∠FDC=45°，
∴∠DFC=90°，
∵EF//AB，
∴∠EFC=∠BAC=45°，∠FEC=∠B=67.5°，
∴∠EFD=∠EFC+∠DFC=135°，
∴∠FED＝∠FDE＝22.5°，
∵∠FDC＝45°，
∴∠CDE=∠FDC-∠FDE=22.5°，
∴∠FDE=∠CDE，
∴DE平分∠FDC，故③正确；
∵AB＝AC，∠CAB＝45°，
∴∠B＝∠ACB＝67.5°，
∴∠DEC＝∠FEC﹣∠FED＝45°，故④错误；
∵△ACD是等腰直角三角形，
∴AC2=2CD2，
∴AC=CD，
∵AB=AC，
∴AB＝CD，故⑤正确；
故答案为：①②③⑤．
本题考查的是三角形中位线定理，等腰三角形的判定与性质，直角三角形的性质，平行线的性质，勾股定理等知识．掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．
13、a（3+a）（3﹣a）．
【解析】
先提公因式，再用平方差公式，可得答案．
【详解】
原式=a（9﹣a2）=a（3+a）（3﹣a）．
故答案为：a（3+a）（3﹣a）．
本题考查了因式分解，利用提公因式与平方差公式是解题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）;（2）的值为.
【解析】
（1）设直线AB所对应的函数表达式为.把点和点.代入，用待定系数法求解即可；
（2）把代入（1）中求得的解析式即可求出m的值.
【详解】
（1）直线经过点和点，
解得
直线所对应的函数表达式为．
（2）当时，．
的值为.
本题考查了待定系数法求函数解析式及一次函数图像上点的坐标特征，熟练掌握待定系数法是解答本题的关键.
15、x≤－1
【解析】
分析：去分母、去括号，移项合并同类项，然后求得解集．
详解：去分母得：6﹣3（3﹣x）≥2（2x﹣1）
去括号得： 6﹣9＋3x≥4x﹣2
解得：x≤－1．
原不等式的解集在数轴上表示如下：
点睛：本题考查了解一元一次不等式、在数轴上表示不等式的解集．把不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画）．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．
16、（1） 0.2；（2）
【解析】
（1）根据题意可知客厅中心的正方形边长为 4m， 再结合图形即可求得回字型黑色边框的宽度；
（2）根据白色瓷砖区域Ⅱ的面积由四个全等的长方形及客厅中心的正方形组成，可得关于x的方程，解方程后进行讨论即可得答案.
【详解】
（1）由已知可得客厅中心的正方形边长为 4m，
由图可得边框宽度为  6  4  0.8  2  0.2 m，
即回字型黑色边框的宽度为0.2m；
（2）由已知可列方程：4x6  2x 16  26，
解得：x1＝ ，x2＝ ，
当 x＝时， 2  4  9 ＞6，不符合实际，舍去，
∴x＝.
本题考查了一元二次方程的应用，弄清题意，找出等量关系列出方程是解题的关键.
17、（1）详见解析；（2）详见解析；（3）．
【解析】
（1）先根据两直线平行内错角相等得出，再根据E为BD中点，和对顶角相等，根据AAS证出≌，从而证出；
（2）根据对角线互相平分的四边形是平行四边形，得出四边形ABCD是平行四边形，证出，，在结合已知条件，根据一组对边平行且相等的四边形是平行四边形，从而证出结论；
（3）根据平行四边形的对角相等得出，再根据得出，根据勾股定理得出，从而得出四边形ABDF的面积；
【详解】
证明，
，
，，
≌，
；
由可知，，
四边形ABCD是平行四边形，
，，
，
，，
四边形ABDF为平行四边形；
四边形ABDF为平行四边形，
，AF=BD=2,
，，
，
，
，
根据勾股定理可得： ，
四边形ABDF的面积．
本题考查了平行四边形的性质和判定，全等三角形的性质和判定以及勾股定理等知识点，熟练掌握相关的知识是解题的关键．
18、（1），；（2）
【解析】
（1）将代入求得m,确定一个解析式；由P点在x轴上，即纵坐标为0，确定P的坐标，再结合顶点式，即可确定第二个解析式；
（2）由（1）得到得解析式，然后列出不等式，解不等式即可.
【详解】
（1）把代入，
∴，
∴，
∴，
∴令，，
∴，
∴，
∵抛物线的顶点为，
∴设抛物线.
代入得，
∴，
即.
（2）由题意得：x+1＜
解得：.
本题主要考查了待定系数法确定解析式和解不等式，其中解不等式是解答本题的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、，．
【解析】
方程变形得：x1+1x=0，即x（x+1）=0，
可得x=0或x+1=0，
解得：x1=0，x1=﹣1．
故答案是：x1=0，x1=﹣1.
20、（3，0）或（﹣3，0）
【解析】
试题解析：设点C到原点O的距离为a，
∵AC+BC=6，
∴a-+a+=6，
解得a=3，
∴点C的坐标为（3，0）或（-3，0）．
21、3
【解析】
由菱形性质得AC⊥BD,BO= ,AO=,由勾股定理得AO= ,由中位线性质得EF=.
【详解】
因为，菱形ABCD中，对角线AC，BD相交于点O，
所以，AC⊥BD,BO= ,AO=,
所以，AO= ,
所以，AC=2AO=6,
又因为E，F分别是的边AB，BC边的中点
所以，EF=.
故答案为3
本题考核知识点：菱形，勾股定理，三角形中位线.解题关键点：根据勾股定理求出线段长度，再根据三角形中位线求出结果.
22、1
【解析】
利用平行四边形的对角相等、邻角互补可求得答案．
【详解】
解：因为四边形ABCD是平行四边形，
所以∠B＝∠D，∠A+∠B＝180°．
因为∠B+∠D＝190°，
所以∠B＝95°．
所以∠A＝180°﹣95°＝1°．
故答案为1．
此题考查平行四边形的性质，解题关键在于掌握其性质定理
23、2.
【解析】
将点（2，3）代入y=kx+k-3可得关于k的方程，解方程求出k的值即可．
【详解】
将点(2,3)代入一次函数y=kx+k−3，
可得：3=2k+k−3，
解得：k=2.
故答案为2.
本题考查了一次函数的性质.
二、解答题（本大题共3个小题，共30分）
24、4﹣1
【解析】
先根据二次根式的乘法、除法法则计算、去绝对值符号，再合并同类二次根式即可得．
【详解】
解：原式＝1+-(1-)
＝3-1+
＝4-1．
本题主要考查二次根式的混合运算，解题的关键是掌握二次根式的混合运算顺序和运算法则及绝对值的性质．
25、12m
【解析】
根据题意得出在Rt△ABC中，BC=即可求得.
【详解】
如图所示：
由题意可得，AB=5m，AC=13m，
在Rt△ABC中，BC==12（m），
答：这条缆绳在地面的固定点距离电线杆底部12m．
要考查了勾股定理的应用，根据题意得出△ABC是直角三角形是解题关键,再运用勾股定理求得BC的值．
26、甲小区住户有175户，乙小区住户有50户
【解析】
设乙小区住户为x户，则甲小区住户有：（3x+25）户，根据每户平均收到资料的数量相同，列出方程，解答即可.
【详解】
解：设乙小区住户为x户，
根据题意得：，
解得：，
经检验是原方程的解，
∴甲小区住户，
所以，甲小区住户有175户，乙小区住户有50户．
本题考查了分式方程的实际应用，解题的关键是找到题目中的关系，列出分式方程.
题号
一
二
三
四
五
总分
得分
批阅人
时间（单位：小时）
4
3
2
l
0
人数
3
4
1
1
1