北师大版八年级数学上册专题1.3勾股定理的实际应用【十二大题型】同步练习(学生版+解析)

这是一份北师大版八年级数学上册专题1.3勾股定理的实际应用【十二大题型】同步练习(学生版+解析)，共58页。

TOC \ "1-3" \h \u
\l "_Tc11833" 【题型1 求梯子滑落高度】 PAGEREF _Tc11833 \h 1
\l "_Tc12733" 【题型2 求旗杆高度】 PAGEREF _Tc12733 \h 3
\l "_Tc32411" 【题型3 求小鸟飞行距离】 PAGEREF _Tc32411 \h 4
\l "_Tc21489" 【题型4 求大树折断前的高度】 PAGEREF _Tc21489 \h 5
\l "_Tc6542" 【题型5 解一元一次不等式组】 PAGEREF _Tc6542 \h 7
\l "_Tc19332" 【题型6 解决水杯中筷子问题】 PAGEREF _Tc19332 \h 8
\l "_Tc29230" 【题型7 解决航海问题】 PAGEREF _Tc29230 \h 9
\l "_Tc14785" 【题型8 求河宽】 PAGEREF _Tc14785 \h 10
\l "_Tc7365" 【题型9 求台阶上地毯长度】 PAGEREF _Tc7365 \h 12
\l "_Tc16685" 【题型10 判断汽车是否超速】 PAGEREF _Tc16685 \h 13
\l "_Tc15245" 【题型11 选址使到两地距离相等】 PAGEREF _Tc15245 \h 14
\l "_Tc26074" 【题型12 求最短路径】 PAGEREF _Tc26074 \h 15
【题型1 求梯子滑落高度】
【例1】（2023春·广东惠州·八年级校考期中）某地一楼房发生火灾，消防队员决定用消防车上的云梯救人如图（1），如图（2），已知云梯最多只能伸长到15m（即AB=CD=15m），消防车高3m，救人时云梯伸长至最长，在完成从12m（即BE=12m）高的B处救人后，还要从15m（即DE=15m）高的D处救人，这时消防车从A处向着火的楼房靠近的距离AC为多少米？（延长AC交DE于点O，AO⊥DE，点B在DE上，OE的长即为消防车的高3m）
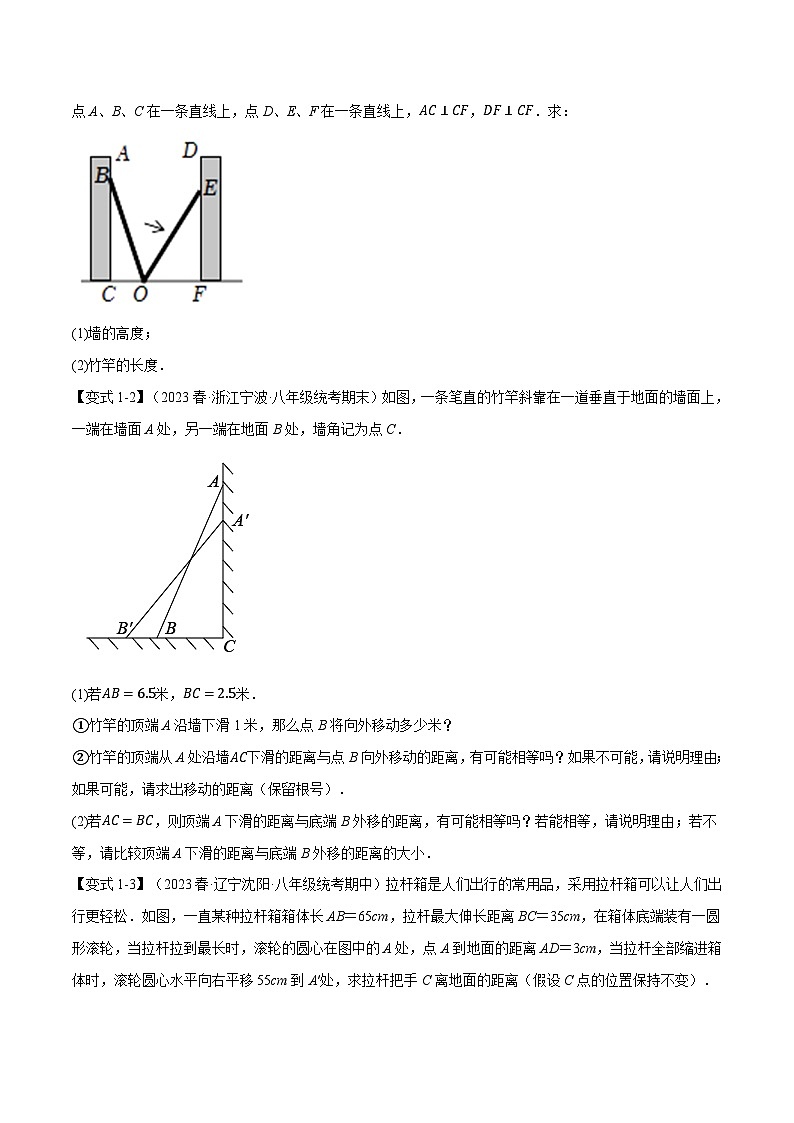
【变式1-1】（2023春·山西晋中·八年级统考期中）如图，小巷左右两侧是竖直的高度相等的墙，一根竹竿斜靠在左墙时，竹竿底端O到左墙角的距离OC为0.7米，顶端B距墙顶的距离AB为0.6米若保持竹竿底端位置不动，将竹竿斜靠在右墙时，竹竿底端到右墙角的距离OF为1.5米，顶端E距墙项D的距离DE为1米，点A、B、C在一条直线上，点D、E、F在一条直线上，AC⊥CF，DF⊥CF．求：
(1)墙的高度；
(2)竹竿的长度．
【变式1-2】（2023春·浙江宁波·八年级统考期末）如图，一条笔直的竹竿斜靠在一道垂直于地面的墙面上，一端在墙面A处，另一端在地面B处，墙角记为点C．
(1)若AB=6.5米，BC=2.5米．
①竹竿的顶端A沿墙下滑1米，那么点B将向外移动多少米？
②竹竿的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？如果不可能，请说明理由；如果可能，请求出移动的距离（保留根号）．
(2)若AC=BC，则顶端A下滑的距离与底端B外移的距离，有可能相等吗？若能相等，请说明理由；若不等，请比较顶端A下滑的距离与底端B外移的距离的大小．
【变式1-3】（2023春·辽宁沈阳·八年级统考期中）拉杆箱是人们出行的常用品，采用拉杆箱可以让人们出行更轻松．如图，一直某种拉杆箱箱体长AB＝65cm，拉杆最大伸长距离BC＝35cm，在箱体底端装有一圆形滚轮，当拉杆拉到最长时，滚轮的圆心在图中的A处，点A到地面的距离AD＝3cm，当拉杆全部缩进箱体时，滚轮圆心水平向右平移55cm到A′处，求拉杆把手C离地面的距离（假设C点的位置保持不变）．
【题型2 求旗杆高度】
【例2】（2023春·山西临汾·八年级统考期末）同学们想利用升旗的绳子、卷尺，测算学校旗杆的高度．爱动脑的小华设计了这样一个方案：如图，将升旗的绳子拉直刚好触底，此时测得绳子末端C到旗杆AB的底端B的距离为1米，然后将绳子末端拉直到距离旗杆5米的点E处，此时测得绳子末端E距离地面的高度DE为1米．请你根据小华的测量方案和测量数据，求出学校旗杆的高度．
【变式2-1】（2023春·江西景德镇·八年级统考期中）2021年是中国共产党建党100周年，大街小巷挂满了彩旗．如图是一面长方形彩旗完全展平时的尺寸图（单位：cm）．其中长方形ABCD是由双层白布缝制的穿旗杆用的旗裤，阴影部分DCEF为长方形绸缎旗面，将穿好彩旗的旗杆垂直插在地面上．旗杆从旗顶到地面的高度为240cm，在无风的天气里，彩旗自然下垂．求彩旗下垂时最低处离地面的最小高度h．
【变式2-2】（2023春·八年级课时练习）太原的五一广场视野开阔，是一处设计别致，造型美丽的广场园林，成为不少市民放风筝的最佳场所，某校八年级（1）班的小明和小亮同学学习了“勾股定理”之后，为了测得图中风筝的高度CE，他们进行了如下操作：
①测得BD的长为15米（注：BD⊥CE）；
②根据手中剩余线的长度计算出风筝线BC的长为25米；
③牵线放风筝的小明身高1.7米．
(1)求风筝的高度CE．
(2)过点D作DH⊥BC，垂足为H，求BH的长度．
【变式2-3】（2023春·山西吕梁·八年级统考期中）如图，一根直立的旗杆高8米，一阵大风吹过，旗杆从点C处折断，顶部（B）着地，离旗杆底部（A）4米，工人在修复的过程中，发现在折断点C的下方1.25米D处，有一明显裂痕，若下次大风将旗杆从D处吹断，则距离旗杆底部周围多大范围内有被砸伤的危险？
【题型3 求小鸟飞行距离】
【例3】（2023春·陕西咸阳·八年级统考期中）如图，一只小鸟旋停在空中A点，A点到地面的高度AB=20米，A点到地面C点（B、C两点处于同一水平面）的距离AC=25米．若小鸟竖直下降12米到达D点（D点在线段AB上），求此时小鸟到地面C点的距离．
【变式3-1】（2023春·八年级课时练习）有两棵树，一棵高6米，另一棵高3米，两树相距4米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了（ ）米．
A．3B．4C．5D．6
【变式3-2】（2023春·山东枣庄·八年级统考期中）有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m的一棵大树上，大树高14m，且巢离树顶部1m．当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s，那它至少需要多少时间才能赶回巢中？
【变式3-3】（2023春·贵州贵阳·八年级校考期中）假期中，小明和同学们到某海岛上去探宝，按照探宝图，他们从A点登陆后先往东走8千米，又往北走2千米，遇到障碍后又往西走了3千米，再折向北走了6千米处往东一拐，仅走了1千米就找到宝藏，问登陆点A到宝藏埋藏点B的直线距离是多少千米？
【题型4 求大树折断前的高度】
【例4】（2023春·八年级课时练习）如图，在倾斜角为45°（即∠NMP=45°）的山坡MN上有一棵树AB，由于大风，该树从点E处折断，其树顶B恰好落在另一棵树CD的根部C处，已知AE=1m， AC=18m．
(1)求这两棵树的水平距离CF；
(2)求树AB的高度．
【变式4-1】（2023春·广东云浮·八年级统考期中）海洋热浪对全球生态带来了严重影响，全球变暖导致华南地区汛期更长、降水强度更大，使得登录广东的台风减少，但是北上的台风增多．如图，一棵大树在一次强台风中距地面5m处折断，倒下后树顶端着地点A距树底端B的距离为12m，这棵大树在折断前的高度为（ ）

A．10mB．15mC．18mD．20m
【变式4-2】（2023春·山西阳泉·八年级统考期末）我国古代数学名著《算法统宗》有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地．送行二步与人齐，5尺人高曾记，仕女家人争蹴．良工高士素好奇，算出索长有几？”此问题可理解为：“如图，有一架秋千，当它静止时，踏板离地距离PA的长为1尺，将它向前水平推送10尺时，即P'C=10尺，秋千踏板离地的距离P'B和身高5尺的人一样高，秋千的绳索始终拉得很直，试问绳索有多长？”，设秋千的绳索长为x尺，根据题意可列方程为 ．
【变式4-3】（2023春·广东珠海·八年级校考期中）如图，一根直立的旗杆高8m,因刮大风旗杆从点C处折断，顶部B着地且离旗杆底部A4m.
（1）求旗杆距地面多高处折断；
（2）工人在修复的过程中，发现在折断点C的下方1.25m的点D处，有一明显裂痕，若下次大风将旗杆从点D处吹断，则距离旗杆底部周围多大范围内有被砸伤的危险？
【题型5 判断是否受台风影响】
【例5】（2023春·湖北武汉·八年级统考期中）如图，铁路MN和公路PQ在点O处交汇，∠QON=30°，公路PQ上A处距离O点240米，如果火车行驶时，火车头周围150米以内会受到噪音的影响，那么火车在铁路MN上沿MN方向以72千米/小时的速度行驶时，A处受到噪音影响的时间为 秒．
【变式5-1】（2023春·陕西西安·八年级统考期中）为了鼓励大家积极接种新冠疫苗，某区镇政府采用了移动宣讲的形式进行广播宣传．如图，笔直的公路MN的一侧点A处有一村庄，村庄到公路MN的距离为300m，宣讲车P周围500m以内能听到广播宣传，宣讲车P在公路上沿MN方向行驶．
(1)村庄能否听到广播宣传？请说明理由．
(2)已知宣讲车的速度是50m/min，如果村庄能听到广播宣传，那么总共能听多长时间？
【变式5-2】（2023春·山东青岛·八年级校考期末）如图所示，在甲村至乙村的公路AB旁有一块山地正在开发，现需要在C处进行爆破，已知点C与公路上的停靠站A的距离为300米，与公路上的另一停靠站B的距离为400米，且CA⊥CB．为了安全起见，爆破点C周围半径250米范围内不得进入，在进行爆破时，公路AB是否有危险而需要封锁？如果需要，请计算需要封锁的路段长度；如果不需要，请说明理由．
【变式5-3】（2023春·广东广州·八年级校考期中）如图，A城气象台测得台风中心在A城正西方向320 km的B处，以每小时40 km的速度向北偏东60°的BF方向移动，距离台风中心200 km的范围内是受台风影响的区域．
(1)A城是否受到这次台风的影响？为什么？
(2)若A城受到这次台风影响，则A城遭受这次台风影响有多长时间？
【题型6 解决水杯中筷子问题】
【例6】（2023春·河北唐山·八年级统考期中）如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条长16cm的直吸管露在罐外部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）

A．4