湖北省武汉市光谷外国语学校2024-2025学年上学期九年级数学9月考试xc+

这是一份湖北省武汉市光谷外国语学校2024-2025学年上学期九年级数学9月考试xc+，共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题(共10小题，每小题3分，共30分)
1. 方程 2x²-3x-1=0的二次项系数和一次项系数分别为( ).
A. 2x²和-3x B. 2x²和3x C. 2和-3 D. 2和3
2. 一元二次方程 x²-2x=0的根为( ).
A.x₁=0或 x₂=-2 B.x₁=2或 x₂=-2 C.x₁=0或 x₂=2 D. x=2
3. 若一元二次方程 x²-3x+a=0的一个根为x=2, 则a的值为 ( ).
A. 2 B. -2 C. 4 D. -4
4. 抛物线 y=x²-2mx+3的对称轴为直线x=2，则m的值为( ).
A. -2 B. 2 C. -4 D. 4
5. 一元二次方程 x²-5x-2=0的根的判别式的值为( ).
A. 17 B.17 C. 33 D.33
6. 抛物线 y=x-2²+2的顶点坐标是( ).
A. (2, -2) B. (2, 2) C. (-2, -2) D. (-2, 2)
7. 将 x²+4x-5=0进行配方变形，下列正确的是 ( ).
A.x+2²=9 B.x-2²=9 C.x+2²=1 D.x-2²=1
8. 已知A (-1, y₁), B (2, y₂), C(4, y₃) 是二次函数. y=-x²+2x+c的图象上的三个点，则y₁，y₂，y₃的大小关系为( ).
A. y₁9. 将抛物线 y=-2x+1²-2向左平移2个单位，向下平移3个单位后的新抛物线解析式为( ).
A.y=-2x-1²+1 B.y=-2x+3²-5
C.y=-2x-1²-5 D.y=-2x+3²+1
10. 抛物线 y=ax²+bx+ca≠0上部分点的坐标如下表，下列说法错误的是( ).
A. 对称轴是直线x=-2 B. 当x=-4时, y=-11
C. 当x>-2时, y随x的增大而减小 D. 抛物线开口向下
二、填空题 (共6小题，每小题3分，共18分)
11. 方程(x+3)(x-2) =0化为一元二次方程的一般形式是 .
12. 二次函数 y=x²-2x+2的最小值是 .
13. 关于x的一元二次方程 ax²+bx+6=0的一个根是3, 则3a+b= .
14. 抛物线 y=ax²+bx+c的部分图象如图所示，则当y>0时，x的取值范围是 .
第 1 页 共 4 页x

--3
--2
--1
0
1

y

--3
--2
--3
--6
-11

15. 若关于x的二次方程 m+2x²+x+m²-4=0的常数项等于0，则m的值为 .
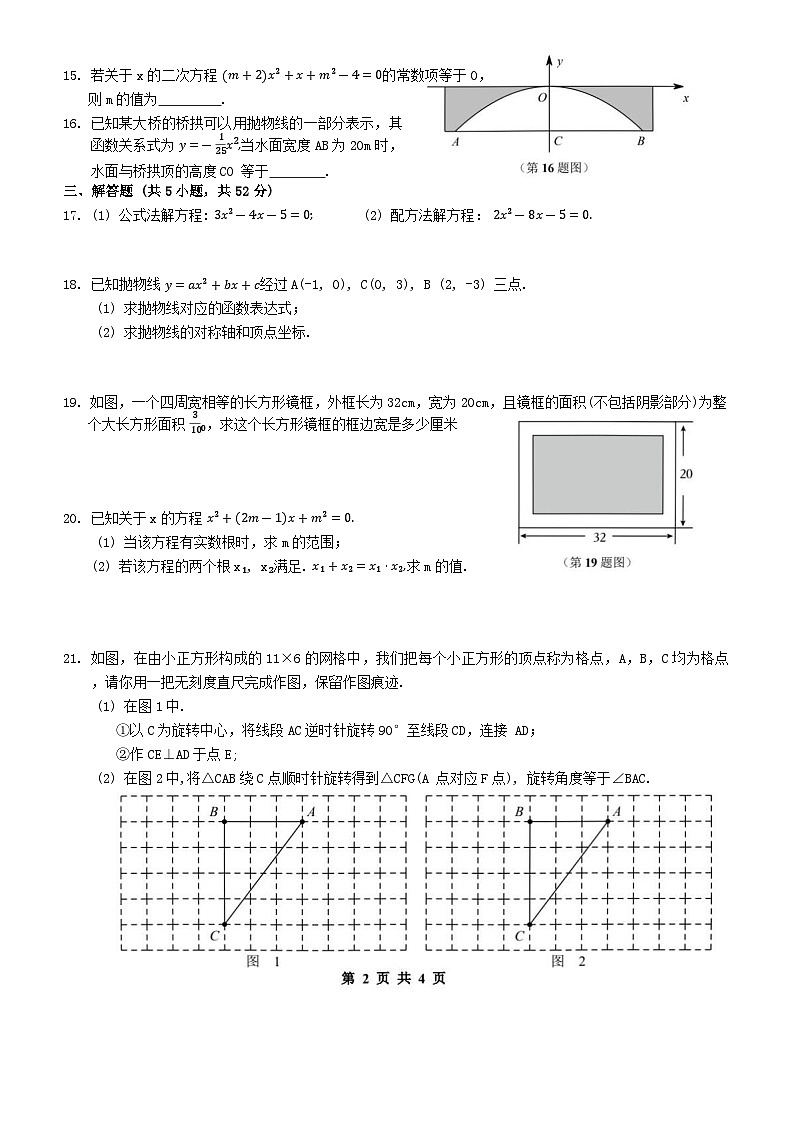
16. 已知某大桥的桥拱可以用抛物线的一部分表示，其函数关系式为 y=-125x2,当水面宽度AB为20m时，水面与桥拱顶的高度CO 等于 .
三、解答题 (共5小题，共52分)
17. (1) 公式法解方程: 3x²-4x-5=0; (2) 配方法解方程： 2x²-8x-5=0.
18. 已知抛物线 y=ax²+bx+c经过A(-1, 0), C(0, 3), B (2, -3) 三点.
(1) 求抛物线对应的函数表达式；
(2) 求抛物线的对称轴和顶点坐标.
19. 如图，一个四周宽相等的长方形镜框，外框长为32cm，宽为20cm，且镜框的面积(不包括阴影部分)为整个大长方形面积 310₀，求这个长方形镜框的框边宽是多少厘米
20. 已知关于x的方程 x²+2m-1x+m²=0.
(1) 当该方程有实数根时，求m的范围；
(2) 若该方程的两个根x₁, x₂满足. x₁+x₂=x₁⋅x₂,求m的值.
21. 如图，在由小正方形构成的11×6的网格中，我们把每个小正方形的顶点称为格点，A，B，C均为格点，请你用一把无刻度直尺完成作图，保留作图痕迹.
(1) 在图1中.
①以C为旋转中心，将线段AC逆时针旋转90°至线段CD，连接 AD；
②作CE⊥AD于点E;
(2) 在图2中,将△CAB绕C点顺时针旋转得到△CFG(A 点对应F点), 旋转角度等于∠BAC.
四、填空题 (共6小题，每小题3分，共18分)
22. 关于x的一元二次方程 x²-2x-m=0的两个实根分别为α, β, 且α+2β=5, 则m的值为 .
23. 某学校开办篮球赛，规定每两个球队间都要进行一场比赛，共要比赛15场，设参加比赛的球队有x支，根据题意，列出的方程是 .
24. 在平面直角坐标系中, 将点 A(3, 3₃)绕点 O逆时针旋转 150°得到点 B，则点 B 的坐标为 .
25. 已知点 P (m, n) 在二次函数 y=x²+2x-3的图象上，且点 P 到y 轴的距离小于 2，则n 的取值范围 是 .
26. 关于x的一元二次方程 x²-m+2x-3m-3=0在--2≤x≤2范围内有且只有一个根，则m的取值范围为 .
27. 已知二次函数 y=ax²+bx+c(a<0)的图象与x轴的一个交点坐标为(-1，0)，对称轴为直线x=1，下列结论中：
①a-b+c=0;
②若P为常数，则方程 ax+1x-3+p²=0定有两个不相等的实数根；/
③若m为任意实数，则( am²-bm≥a-b;
④若 m其中正确结论有 .(只需填写正确结论的序号)
五、解答题(共3小题，共32分)
28. 如图，灌溉车为绿化带浇水，喷水口H离地面的竖直高度 OH为1.2m. 若把灌溉车喷出水的上、下边缘抽象为坐标系中两条抛物线的部分图象； 把绿化带横截面抽象为矩形 DEFG，其水平宽度 DE=2.5m，竖直高度 EF=0.7m，H点是下边缘抛物线的最高点，下边缘喷水的最大射程OB=2m，上边缘抛物线最高点A离喷水口的水平距离为2m，高出喷水口0.4m，灌溉车到绿化带的距离 OD为 dm.
(1) 直接写出上、下边缘抛物线的函数解析式；(不需要写出自变量的取值范围)
(2)此时，距离喷水口水平距离为6.5米的地方正好有一个行人经过，试判断该行人是否会被洒水车淋到水? 并写出你的判断过程；
(3) 要使灌溉车行驶时喷出的水能浇灌到整个绿化带，直接写出d的取值范围.
第 3 页 共 4 页
29. 如图, 在等腰Rt△ABC中, ∠BAC=90°, AB=AC, D、E 分别为斜边 BC 上的两动点, BD=CE.
(1) 如图1, 若EH⊥AD于点 H, 延长EH交AB于点K, 求证: AE=EK;
(2)如图2,过点E作 EF∥AD交边AC于点 F, 以AF为斜边在直线AC的右侧作等腰Rt△GAF,求证， AD+EF=2CG;
(3)如图3, 若AB=4,将线段 AE绕点 E 顺时针旋转90°得 EM, N为BM中点,当 AN+12AM取得最小值时，请直接写出△ACD 的面积为 .
30. 如图1, 抛物线 y=ax-1²+b与x轴交于A、B两点(A点在B 点左侧)，与y轴负半轴交于 C点，若AB=4, 且OC=OB.
(1) 求该抛物线的函数解析式；
(2)如图2，P点在第四象限内的抛物线上，且CB平分∠ACP，求点 P的坐标；
(3)如图3，直线x=h与线段OB交于点 H，与抛物线交于点G，动点 P在B、G两点之间的抛物线上，直线AP、BP 与直线x=h分别交于M、N两点, 若HM+3HN恒为定值, 求h的值.
第 4 页 共 4 页