辽宁省灯塔市2023年八年级数学第一学期期末检测试题【含解析】

这是一份辽宁省灯塔市2023年八年级数学第一学期期末检测试题【含解析】，共20页。试卷主要包含了下列各组数中，是方程的解的是，下列从左到右的变形，估计的运算结果应在，若，则的值为等内容，欢迎下载使用。

1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题（每题4分，共48分）
1．下列计算中正确的是( )
A．B．C．D．
2．八年级学生去距学校s千米的博物馆参观，一部分同学骑自行车先走，过了1小时后，其余同学乘汽车出发，结果他们同时到达．已知汽车的速度是骑车同学速度的m倍，设骑车同学的速度为x千米/小时，则可列方程（ ）
A．=+1B．-=1C．=+1D．=1
3．下面的计算过程中，从哪一步开始出现错误( )．
A．①B．②C．③D．④
4．如图，在Rt△ABC中，∠B=90°，D是BC延长线上一点，∠ACD=130°，则∠A等于（ ）
A．40°B．50°C．65°D．90°
5．用下列长度的三条线段,能组成一个三角形的是( )
A．B．C．D．
6．下列各组数中，是方程的解的是（ ）
A．B．C．D．
7．下列从左到右的变形：；；；其中，正确的是
A．B．C．D．
8．估计的运算结果应在（ ）
A．3到4之间B．4到5之间C．5到6之间D．6到7之间
9．如图， 中，垂直平分交于点，交于点.已知的周长为的周长为，则的长（ ）
A．B．C．D．
10．若，则的值为（ ）
A．1B．C．D．
11．一个多边形的内角和是外角和的4倍，则这个多边形是( )
A．七边形B．八边形C．九边形D．十边形
12．下列说法正确的是（ ）
A．若ab＝0，则点P（a，b）表示原点
B．点（1，﹣a2）一定在第四象限
C．已知点A（1，﹣3）与点B（1，3），则直线AB平行y轴
D．已知点A（1，﹣3），AB∥y轴，且AB＝4，则B点的坐标为（1，1）
二、填空题（每题4分，共24分）
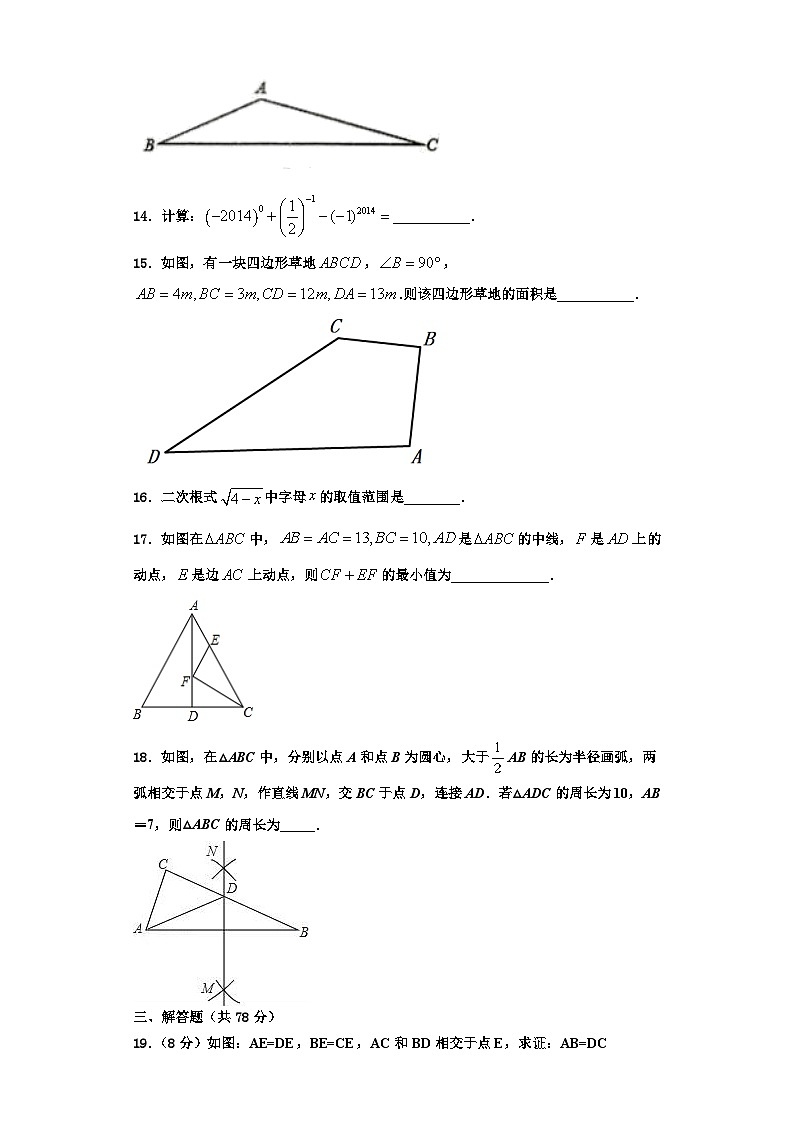
13．如图，在中，则，的面积为__________．
14．计算：___________．
15．如图，有一块四边形草地，，.则该四边形草地的面积是___________．
16．二次根式中字母的取值范围是________．
17．如图在中，是的中线，是上的动点，是边上动点，则的最小值为______________．
18．如图，在△ABC中，分别以点A和点B为圆心，大于AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB＝7，则△ABC的周长为_____．
三、解答题（共78分）
19．（8分）如图：AE=DE，BE=CE，AC和BD相交于点E，求证：AB=DC
20．（8分）如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于E、F.
(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC，其他条件不变，图中还有等腰三角形吗?如果有，分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
21．（8分）如图是由36个边长为1的小正方形拼成的网格图，请按照要求画图：
（1）在图①中画出2个以AB为腰且底边不等的等腰△ABC，要求顶点C是格点；
（2）在图②中画出1个以AB为底边的等腰△ABC，要求顶点C是格点．
22．（10分）快车从M地出发沿一条公路匀速前往N地，慢车从N地出发沿同一条公路匀速前往M地，已知快车比慢车晚出发0.5小时，快车先到达目的地．设慢车行驶的时间为t（h），快慢车辆车之间的距离为s（km），s与t的函数关系如图1所示．
（1）求图1中线段BC的函数表达式；
（2）点D的坐标为 ，并解释它的实际意义；
（3）设快车与N地的距离为y（km），请在图2中画出y关于慢车行驶时间t的函数图象．（标明相关数据）
23．（10分）如图，为等边三角形，平分交于点，交于点．
（1）求证：是等边三角形．
（2）求证：．
24．（10分）如图,在中,,且,点是线段上一点,且,连接BE.
(1)求证:
(2)若,求的度数.
25．（12分）如图所示，
（1）写出顶点的坐标．
（2）作关于轴对称的
（3）计算的面积．
26．如图1，将一个长为4a，宽为2b的长方形，沿图中虚线均匀分成4个小长方形，然后按图2形状拼成一个正方形．
（1）图2的空白部分的边长是多少？（用含ab的式子表示）
（2）若，求图2中的空白正方形的面积．
（3）观察图2，用等式表示出，ab和的数量关系．
参考答案
一、选择题（每题4分，共48分）
1、D
【分析】运用幂的运算法则即可进行判断．
【详解】A中和不是同底数幂，也不是同类项，不能合并，A错；
同底数幂相除，底数不变，指数相减，B错；
同底数幂相乘，底数不变，指数相加，C错；
幂的乘方，底数不变，指数相乘，D对
故本题正确选项为D．
【点睛】
本题考查了幂的运算法则，掌握相关知识点是解决本类题的关键．
2、A
【分析】设骑车同学的速度为x千米/小时，则汽车的速度为mx千米/小时，根据时间=路程÷速度结合骑车的同学比乘车的同学多用1小时，即可得出关于x的分式方程，此题得解．
【详解】设骑车同学的速度为x千米/小时，则汽车的速度为mx千米/小时，
根据题意得：=+1．
故选：A．
【点睛】
本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．
3、B
【解析】直接利用分式的加减运算法则计算得出答案．
【详解】解：
．
故从第②步开始出现错误．
故选：B．
【点睛】
此题主要考查了分式的加减运算，正确掌握相关运算法则是解题关键．
4、A
【详解】∠ACD=∠A+∠B，即130°=∠A+90°，解得∠A=40°.
故选A.
【点睛】
本题考查三角形的一个外角等于与之不相邻的两个内角之和.
5、B
【分析】根据三角形三边关系定理：三角形两边之和大于第三边进行分析．
【详解】解：A、1+2=3，不能组成三角形，故此选项不合题意；
B、2+2＞3，能组成三角形，故此选项符合题意；
C、2+2=4，不能组成三角形，故此选项不符合题意；
D、5+6<12，不能组成三角形，故此选项不合题意；
故选B．
【点睛】
此题主要考查了三角形的三边关系，在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．
6、B
【分析】将四个答案逐一代入,能使方程成立的即为方程的解.
【详解】解:A. ,故错误;
B. ,故正确;
C. ,故错误;
D. ,故错误.
故选:B.
【点睛】
本题考查二元一次方程的解,理解掌握方程的解的定义是解答关键.
7、B
【解析】根据分式的基本性质进行计算并作出正确的判断．
【详解】①，当a=1时，该等式不成立，故①错误；
② ,分式的分子、分母同时乘以b,等式仍成立,即，故②正确；
③，当c=1时，该等式不成立，故③错误；
④,因为x2+1≠1,即分式ab的分子、分母同时乘以(x2+1),等式仍成立,即成立，故④正确；
综上所述，正确的②④.
故选：B.
【点睛】
本题考查了分式的基本性质，注意分式的基本性质中分子、分母乘以（或除以）的数或式子一定不是1．
8、A
【分析】根据算术平方根的定义由9＜15＜16可得到31．
【详解】解：∵9＜15＜16，
∴31．
故选：A．
【点睛】
本题考查了估算无理数的大小：利用完全平方数和算术平方根对无理数的大小进行估算．
9、A
【分析】首先依据线段垂直平分线的性质得到AE=CE；接下来，依据AE=CE可将△ABE的周长为:14转化为AB+BC=14，求解即可.
【详解】∵DE是AC的垂直平分线，
∴AE=CE，
∴△ABE的周长为:AB+BE+AE=AB+BE+CE=AB+BC
∵的周长为的周长为
∴AB+BC=14
∴AC=24-14=10
故选：A
【点睛】
本题主要考查的是线段垂直平分线的性质，掌握线段垂直平分线的性质是解题的关键.
10、D
【解析】∵，
∴==，
故选D
11、D
【分析】先设这个多边形的边数为n，得出该多边形的内角和为（n-2）×180°，根据多边形的内角和是外角和的4倍，列方程求解．
【详解】解：设这个多边形的边数为n，则该多边形的内角和为（n-2）×180°，
依题意得（n-2）×180°=360°×4，
解得n=1，
∴这个多边形的边数是1．
故选：D．
【点睛】
本题主要考查了多边形内角和定理与外角和定理，多边形内角和=（n-2）•180 （n≥3且n为整数），而多边形的外角和指每个顶点处取一个外角，则n边形取n个外角，无论边数是几，其外角和始终为360°．
12、C
【分析】直接利用坐标轴上点的坐标特点以及平行于坐标轴的直线上点的关系分别分析得出答案．
【详解】解：A、若ab＝0，则点P（a，b）表示在坐标轴上，故此选项错误；
B、点（1，﹣a2）一定在第四象限或x轴上，故此选项错误；
C、已知点A（1，﹣3）与点B（1，3），则直线AB平行y轴，正确；
D、已知点A（1，﹣3），AB∥y轴，且AB＝4，则B点的坐标为（1，1）或（1，﹣7），故此选项错误．
故选C．
【点睛】
本题考查了坐标与图形的性质，正确把握点的坐标特点是解题的关键
二、填空题（每题4分，共24分）
13、150
【分析】过点B作BD⊥AC，根据∠A=150°，可得∠BAD=30°，再由AB=20cm，可得BD的长，再根据三角形的面积公式求解即可．
【详解】如图，过点B作BD⊥AC，
∵∠BAC=150°，
∴∠BAD=30°，
∴BD= AB，
∵AB=20，
∴BD=10，
∵S△ABC= AC•BD= ×30×10=150，
故答案为150 .
【点睛】
本题考查含30度角的直角三角形，在直角三角形中，如果有一个角等于30度，那么它所对的直角边等于斜边的一半．
14、1
【分析】分别利用零指数幂和负整数指数幂以及乘方运算化简各项，再作加减法．
【详解】解：
=
=1，
故答案为：1．
【点睛】
本题考查了实数的混合运算，解题的关键是掌握零指数幂和负整数指数幂以及乘方的运算法则．
15、
【分析】连接AC，根据勾股定理求出AC，根据勾股定理的逆定理求出△CAD是直角三角形，分别求出△ABC和△CAD的面积，即可得出答案．
【详解】连结AC，
在△ABC中，
∵∠B＝90°，AB＝4m，BC＝3m，
∴AC＝＝5（m），
S△ABC＝×3×4＝6（m2），
在△ACD中，
∵AD＝13m，AC＝5m，CD＝12m，
∴AD2=AC2+CD2，
∴△ACD是直角三角形，
∴S△ACD＝×5×12＝30（m2）．
∴四边形ABCD的面积＝S△ABC＋S△ACD＝6＋30＝36（m2）
故答案为：．
【点睛】
本题考查了勾股定理，勾股定理的逆定理的应用，解此题的关键是能求出△ABC和△CAD的面积，注意：如果一个三角形的两边的平方和等于第三边的平方，那么这个三角形是直角三角形．
16、
【分析】根据二次根式的定义列不等式求解即可．
【详解】解析：由题意得：，
解得：．
故答案为：．
【点睛】
本题考查了二次根式的定义，形如的式子叫二次根式，熟练掌握二次根式成立的条件是解答本题的关键．
17、
【分析】作E关于AD的对称点M，连接CM交AD于F，连接EF，过C作CN⊥AB于N，根据等腰三角形“三线合一”得出BD的长和AD⊥BC，再利用勾股定理求出AD，利用“等面积法”结合垂线段最短进一步求出最小值即可.
【详解】
如图，作E关于AD的对称点M，连接CM交AD于F，连接EF，过C作CN⊥AB于N，
∵AB=AC=13，BC=10，AD是△ABC的中线，
∴BD=DC=5，AD⊥BC，AD平分∠BAC，
∴M在AB上，
在Rt△ABD中，由勾股定理可得：
AD=，
∴，
∴，
∵E关于AD的对称点M，
∴EF=FM，
∴CF+EF=CF+FM=CM，
根据垂线段最短可得：CM≥CN，
即：CF+EF≥，
∴CF+EF的最小值为：，
故答案为：.
【点睛】
本题主要考查了几何图形中最短路线问题，关键是熟练运用轴对称性质找出相应的线段进行求解.
18、1
【分析】首先根据题意可得MN是AB的垂直平分线，由线段垂直平分线的性质可得AD=BD，再根据△ADC的周长为10可得AC+BC=10，又由条件AB=7可得△ABC的周长．
【详解】解：∵在△ABC中，分别以点A和点B为圆心，大于AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．
∴MN是AB的垂直平分线，
∴AD=BD，
∵△ADC的周长为10，
∴AC+AD+CD=AC+BD+CD=AC+BC=10，
∵AB=7，
∴△ABC的周长为：AC+BC+AB=10+7=1．
故答案为1．
三、解答题（共78分）
19、见详解.
【详解】由SAS可得△ABE≌△DCE，即可得出AB=CD．
∵AE=DE，BE=CE，∠AEB=∠CED（对顶角相等），
∴△ABE≌△DCE（SAS），
∴AB=CD．
20、（1）△AEF、△OEB、△OFC、△OBC、△ABC共5个，EF=BE+FC；（2）有，△EOB、△FOC，存在；（3）有，EF=BE-FC．
【分析】（1）由AB=AC，可得∠ABC=∠ACB；又已知OB、OC分别平分∠ABC、∠ACB；故∠EBO=∠OBC=∠FCO=∠OCB；根据EF∥BC，可得：∠OEB=∠OBC=∠EBO，∠FOC=∠FCO=∠BCO；由此可得出的等腰三角形有：△AEF、△OEB、△OFC、△OBC、△ABC；
已知了△EOB和△FOC是等腰三角形，则EO=BE，OF=FC，则EF=BE+FC．
（2）由（1）的证明过程可知：在证△OEB、△OFC是等腰三角形的过程中，与AB=AC的条件没有关系，故这两个等腰三角形还成立．所以（1）中得出的EF=BE+FC的结论仍成立．
（3）思路与（2）相同，只不过结果变成了EF=BE-FC．
【详解】解：（1）图中是等腰三角形的有：△AEF、△OEB、△OFC、△OBC、△ABC；
EF、BE、FC的关系是EF=BE+FC．理由如下：
∵AB=AC，
∴∠ACB=∠ABC，△ABC是等腰三角形；
∵BO、CO分别平分∠ABC和∠ACB，
∴∠ABO=∠OBC=∠ABC，∠OCB=∠ACO=∠ACB，
∵EF∥BC，
∴∠EOB=∠OBC，∠FOC=∠OCB，
∴∠ABO=∠OBC=∠EOB=∠OCB=∠FOC=∠FCO，
∴△EOB、△OBC、△FOC都是等腰三角形，
∵EF∥BC，
∴∠AEF=∠ABC，∠AFE=∠ACB，
∴∠AEF=∠AFE，
∴△AEF是等腰三角形，
∵OB、OC平分∠ABC、∠ACB，
∴∠ABO=∠OBC，∠ACO=∠OCB；
∵EF∥BC，
∴∠EOB=∠OBC=∠EBO，∠FOC=∠OCB=∠FCO；
即EO=EB，FO=FC；
∴EF=EO+OF=BE+CF；
（2）当AB≠AC时，△EOB、△FOC仍为等腰三角形，（1）的结论仍然成立．
∵OB、OC平分∠ABC、∠ACB，
∴∠ABO=∠OBC，∠ACO=∠OCB；
∵EF∥BC，
∴∠EOB=∠OBC=∠EBO，∠FOC=∠OCB=∠FCO；
即EO=EB，FO=FC；
∴EF=EO+OF=BE+CF；
（3）△EOB和△FOC仍是等腰三角形，EF=BE-FC．理由如下：
同（1）可证得△EOB是等腰三角形；
∵EO∥BC，
∴∠FOC=∠OCG；
∵OC平分∠ACG，
∴∠ACO=∠FOC=∠OCG，
∴FO=FC，故△FOC是等腰三角形；
∴EF=EO-FO=BE-FC．
【点睛】
本题主要考查了等腰三角形的判定和性质，平行线、角平分线的性质等知识．进行线段的等量代换是正确解答本题的关键．
21、（1）答案见解析；（2）答案见解析．
【分析】（1）以A或者B为原点，再作与线段AB相等的线段与格点相交于C，连接ABC 三点即可
（2）作线段AB的中线，中线与格点相交于C，连接ABC 三点即可
【详解】解：（1）
此为所有存在的答案，取其中2个即可
（2）
此为所有存在的答案，取其中1个即可
【点睛】
本题考察了几何画图的能力，掌握等腰三角形的性质，按题意作图即可
22、（1）y＝﹣120x+180；（2）（，90），慢车行驶了小时后，两车相距90千米；（3）详见解析．
【分析】（1）由待定系数法可求解；
（2）先求出两车的速度和，即可求解；
（3）根据函数图象求出快车的速度，从而得y关于慢车行驶时间t的函数解析式，进而即可画出图象．
【详解】（1）设线段BC所在直线的函数表达式为：y＝kx+b（k，b为常数，k≠0）
∴，解得：，
∴线段BC所在直线的函数表达式为：y＝﹣120x+180；
（2）由图象可得：两车的速度和＝＝120（千米/小时），
∴120×（）＝90（千米），
∴点D(，90)，表示慢车行驶了小时后，两车相距90千米；
（3）由函数图象可知：快车从M地到N地花了小时，慢车从N地到M地花了小时，
∴快车与慢车的速度比=：=2：1，
∴快车的速度为：120×=80（千米/小时），M，N之间距离为：80×=140（千米），
∴y关于慢车行驶时间t的函数解析式为： ，
图象如图所示：
【点睛】
本题主要考查一次函数的实际应用，理解函数图象的实际意义，是解题的关键．
23、（1）见解析；（2）见解析
【分析】(1)根据等边三角形的性质和平行线的性质证明即可．
(2)根据等边三角形的性质解答即可．
【详解】(1)∵△ABC为等边三角形，
∴∠A=∠ABC=∠C=60°．
∵DE∥BC，
∴∠AED=∠ABC=60°，∠ADE=∠C=60°．
∴△ADE是等边三角形
(2)∵△ABC为等边三角形，
∴AB=BC=AC．
∵BD平分∠ABC，
∴AD=AC
∵△ADE是等边三角形，
∴AE=AD．
∴AE=AB．
【点睛】
本题考查了等边三角形的判定和性质，关键是根据等边三角形的性质和平行线的性质解答．
24、 (1) 见详解 ； (2) 33°
【分析】(1) 根据题意可得≌ （HL）;
(2) 根据中 得到为等腰直角三角形，得到，根据≌ 得到，即可求出答案.
【详解】(1) ∵
∴ =90°
∵ 在和中

∴≌ （HL）
(2)∵中
∴
∵≌
∴
∵
中,
∴
∵
∴=33° .
【点睛】
此题主要考查了全等三角形的性质和判定及三角形内角度数的计算，熟记概念是解题的关键.
25、（1）（-2，-1）；（2）作图见解析；（3）4.1．
【分析】（1）利用第三象限点的坐标特征写出C点坐标；
（2）利用关于y轴对称的点的坐标特征写出A1、B1、C1的坐标，然后描点即可；
（3）用一个矩形的面积分别减去三个三角形的面积可计算出△ABC的面积．
【详解】（1）C点坐标为（-2，-1）；
（2）如图，△A1B1C1为所作；
（3）△ABC的面积=1×3-×1×2-×2×1-×3×3=4.1．
【点睛】
本题考查了作图-对称轴变换：几何图形都可看做是由点组成，我们在画一个图形的轴对称图形时，也是先从确定一些特殊的对称点开始的．
26、（1）2a－b；(2)25；(3)8ab.
【分析】(1)根据长方形的长是2a，宽是b，可以得到小正方形的边长是长与宽的的差；
(2)从图中可以看出小正方形的面积=大正方形的面积－4个小长方形的面积，再根据2a+b=7求出小正方形的面积；
(3)利用平方差公式得到：，ab和之间的关系．
【详解】解：（1）图2的空白部分的边长是：2a－b；
（2）由图可知，小正方形的面积=大正方形的面积－4个小长方形的面积，
∵大正方形的边长=2a＋b=7，
∴大正方形的面积=，
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24，
∴小正方形的面积=；
（3）由图2可以看出，大正方形的面积=空白部分的正方形的面积+四个小长方形的面积
即：．
考点：1.完全平方公式；2.平方差公式.