专题01+选择填空基础题型：相交线综合题

这是一份专题01+选择填空基础题型：相交线综合题，文件包含专题01选择填空基础题型相交线综合题原卷版docx、专题01选择填空基础题型相交线综合题解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
1．（2023春•海淀区校级期末）如图，图中与是同位角的序号是
A．②③B．②③④C．①②④D．③④
【答案】
【详解】图①中和是同位角，图②中和是同位角，图③中和不是同位角，图④中和是同位角，
故选：．
2．（2023春•平谷区期末）两条直线被第三条直线所截，形成了“三线八角”，为了便于记忆，同学们可仿照图用双手表示“三线八角”（两大拇指代表被截直线，食指代表截线）下列三幅图依次表示
A．同位角、内错角、同旁内角B．同位角、同旁内角、内错角
C．同位角、对顶角、同旁内角D．同位角、内错角、对顶角
【答案】
【详解】两条直线被第三条直线所截，形成了“三线八角”，为了便于记忆，同学们可仿照图用双手表示“三线八角”（两大拇指代表被截直线，食指代表截线）上列三幅图依次表示同位角、内错角、同旁内角，
故选：．
3．（2023春•东城区期末）如图，直线，相交于点，若，，则的度数为
A．B．C．D．
【答案】
【详解】，，
．
故选：．
4．（2023春•海淀区期末）如图，直线与交于点，，若，则的度数为
A．B．C．D．
【答案】
【详解】，
，
，
，
，
故选：．
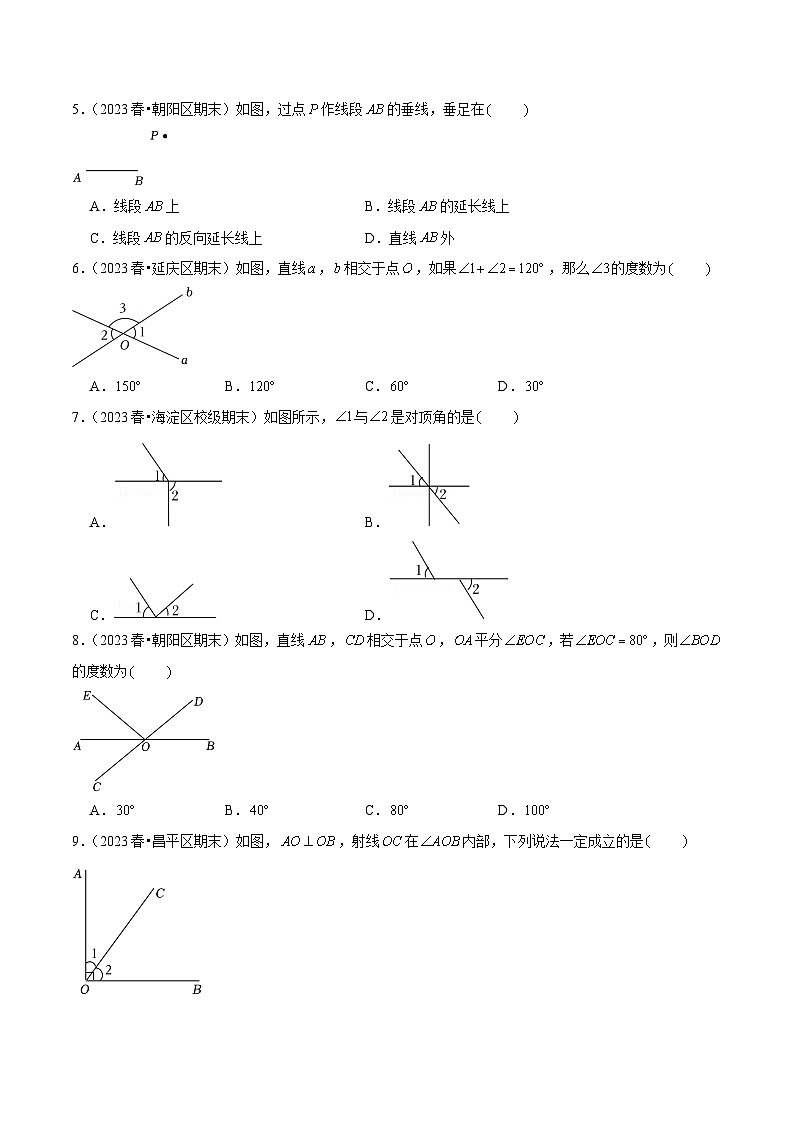
5．（2023春•朝阳区期末）如图，过点作线段的垂线，垂足在
A．线段上B．线段的延长线上
C．线段的反向延长线上D．直线外
【答案】
【详解】如图，
过点作线段的垂线，垂足在线段的延长线上．
故选：．
6．（2023春•延庆区期末）如图，直线，相交于点，如果，那么的度数为
A．B．C．D．
【答案】
【详解】，，
，
又，
，
故选：．
7．（2023春•海淀区校级期末）如图所示，与是对顶角的是
A．B．
C．D．
【答案】
【详解】观察选项，只有选项中的图是对顶角，
故选：．
8．（2023春•朝阳区期末）如图，直线，相交于点，平分，若，则的度数为
A．B．C．D．
【答案】
【详解】平分，
，
，
，
．
故选：．
9．（2023春•昌平区期末）如图，，射线在内部，下列说法一定成立的是
A．和互余B．和互补
C．和互为对顶角D．和相等
【答案】
【详解】，
，
，
和互余．
故选：．
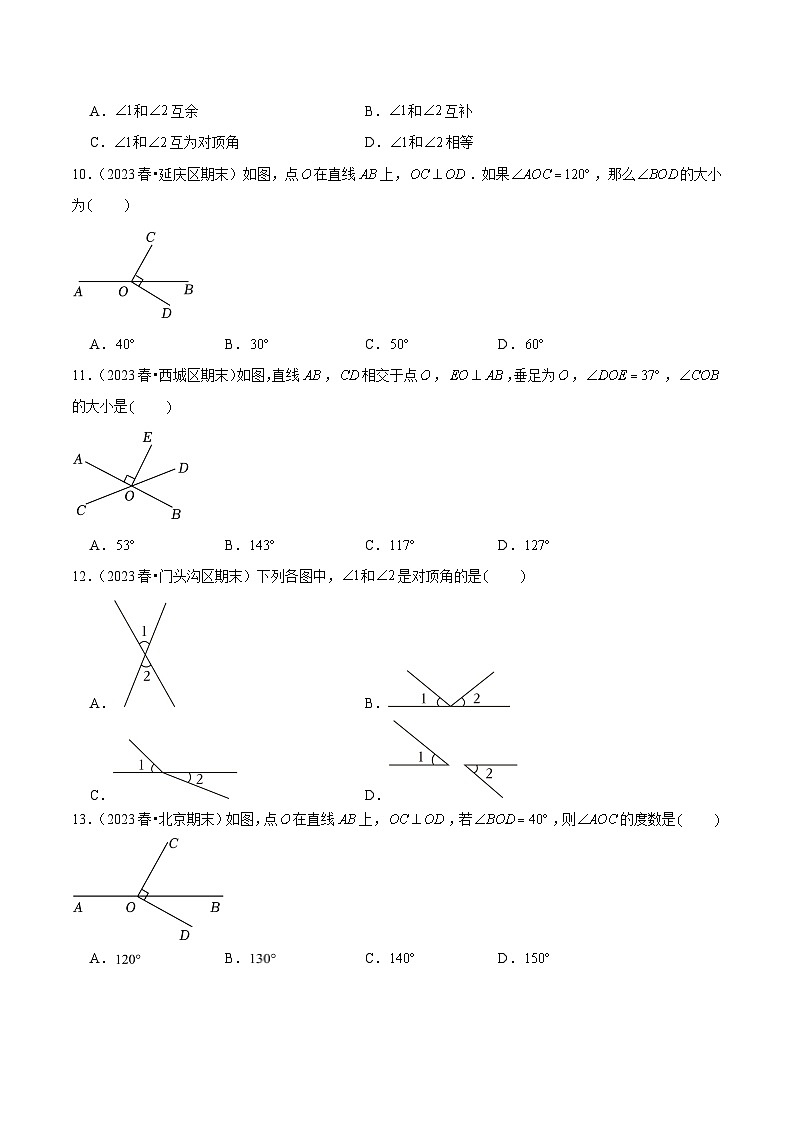
10．（2023春•延庆区期末）如图，点在直线上，．如果，那么的大小为
A．B．C．D．
【答案】
【详解】，，
，
又，
，
，
故选：．
11．（2023春•西城区期末）如图，直线，相交于点，，垂足为，，的大小是
A．B．C．D．
【答案】
【详解】，
，
，
，
．
故选：．
12．（2023春•门头沟区期末）下列各图中，和是对顶角的是
A．B．
C．D．
【答案】
【详解】一个角的两边是另一个角两边的反向延长线，故符合题意；
故选：．
13．（2023春•北京期末）如图，点在直线上，，若，则的度数是
A．B．C．D．
【答案】
【详解】，
，
，
；
，
．
故选：．
14．（2023春•房山区期末）如图，直线，相交于点，，若，则的度数为
A．B．C．D．
【答案】
【详解】，
．
又，
．
故选：．
15．（2023春•东城区期末）如图，直线，相交于点，，垂足为点．若，则的度数为
A．B．C．D．
【答案】
【详解】，
，
，
，
，
故选：．
16．（2022春•西城区校级期末）如图，是上一点，于点，直线经过点，，则的度数为
A．B．C．D．
【答案】
【详解】，
，
，
．
故选：．
17．（2022春•朝阳区期末）下列图形中，和是邻补角的是
A．B．
C．D．
【答案】
【详解】．与是对顶角，故选项不符合题意；
．与是邻补角，故选项符合题意；
．与不存在公共边，不是邻补角，故选项不符合题意；
与是同旁内角，故选项不符合题意；
故选：．
18．（2022春•朝阳区校级期末）如图，直线，相交于点，平分，，若，则的度数为
A．B．C．D．
【答案】
【详解】平分，，
，
与是邻补角，
，
，
，
．
故选：．
19．（2022春•双台子区期末）如图，直线，相交于点，于点．平分，如果，那么的度数
A．B．C．D．
【答案】
【详解】如图，于点．
，
，
，
又，平分，
．
故选：．
20．（2022春•北京期末）如图，点在直线上，．若，则的度数为
A．B．C．D．
【答案】
【详解】，
，
，
，
，
故选：．
21．（2022春•怀柔区校级期末）如图，直线，被所截，下列四个结论：
①和互为对顶角；
②和是同位角；
③；
④和是同旁内角．
其中，结论一定正确的有
A．1个B．2个C．3个D．4个
【答案】
【详解】①和不是对顶角，原说法错误；
②和是同位角，原说法正确；
③与是内错角，但是不一定相等，原说法错误；
④和是同旁内角，原说法正确．
结论一定正确的有2个．
故选：．
22．（2022春•北京期末）如图，直线，相交于点，如果，那么的度数是
A．B．C．D．
【答案】
【详解】和是对顶角，
，
故选：．
23．（2022春•昌平区期末） 如图，若，则的度数是
A．B．C．D．
【答案】
【详解】，
，
即，
，
，
故选：．
24．（2022春•东城区期末）如图，直线与直线相交于点，，，则 )
A．B．C．D．125
【答案】
【详解】，
，
．
故选：．
25．（2022春•房山区期末）若，则的对顶角的大小为
A．B．C．D．
【答案】
【详解】若，则的对顶角的大小为．
故选：．
26．（2022春•西城区校级期末）如图，从位置到直线公路共有四条小道，若用相同的速度行走，能最快到达公路的小道是
A．B．C．D．
【答案】
【详解】根据垂线段最短得，能最快到达公路的小道是，
故选：．
二．填空题（共14小题）
27．（2023春•石景山区期末）为了测量一座古塔外墙底部的底角的度数，李潇同学设计了如下测量方案：作，的延长线，，量出的度数，从而得到的度数．这个测量方案的依据是 ．
【答案】对顶角相等
【详解】这个测量方案的依据是：对顶角相等；
故答案为：对顶角相等．
28．（2023春•西城区期末）如图，在三角形中，，点到直线的距离是线段 的长，的依据是 ．
【答案】，垂线段最短
【详解】，
，
点到直线的距离是线段的长，
根据垂线段最短可得，
故答案为：，垂线段最短．
29．（2023春•大兴区期末）如图，点，，，，在直线上，点在直线外，于点，在线段，，，，中，最短的一条线段是 ，理由是 .
【答案】；垂线段最短
【详解】根据点到直线的距离的定义得出线段的长是点到直线的距离，从直线外一点到这条直线所作的垂线段最短．
故答案为：；垂线段最短．
30．（2023春•平谷区期末）直线、相交于点，，为平面上一点，若，则 ．
【答案】或
【详解】如图1，当在上方时，
，
，
，
；
如图2，当在下方时，
，
，
，
；
综上，的度数为或，
故答案为：或．
31．（2023春•顺义区期末）如图，点在直线上，过点作射线，，．从下面的四个条件中任选两个，可以推出的是 （写出一组满足题意的序号）．
①
②和互余
③
④
【答案】①③
【详解】可以选①③，理由：
，，
，
，，
．
故答案为：①③．
32．（2023春•通州区期末）如图，点在直线上，如果，，那么的度数为 ．
【答案】
【详解】，
，
，
，
，
故答案为：．
33．（2023春•通州区期末）用如图所示方式摆放来测量纸杯角度的数学道理是 ．
【答案】对顶角相等
【详解】根据对顶角相等，故测到的纸杯角度的对顶角就等于纸杯的角度．
故答案为：对顶角相等.
34．（2023春•房山区期末）如图，利用工具测量角，则的大小为 ．
【答案】
【详解】观察量角器可知角的度数为，
由对顶角相等可知，
故答案为：．
35．（2022春•海淀区校级期末）将“对顶角相等”写为“如果，那么”的形式 ．
【答案】如果两个角是对顶角，那么它们相等
【详解】原命题的条件是：“两个角是对顶角”，结论是：“它们相等”，
将“对顶角相等”写成“如果那么”的形式为：“如果两个角是对顶角，那么它们相等”．
故答案为：如果两个角是对顶角，那么它们相等．
36．（2022春•朝阳区期末）如图，，垂足为，平分，则的度数为 ．
【答案】135
【详解】，
，
平分，
，
，
故答案为：135．
37．（2022春•东城区期末）如图，在三角形中，，，，，则点到的距离等于 ．
【答案】3
【详解】根据题意可得，
点到的距离等于3．
故答案为：3．
38．（2022春•北京期末）如图，利用量角器可知的度数为 ．
【答案】
【详解】根据对顶角相等得：，
故答案为：．
39．（2022春•海淀区期末）如图是对顶角量角器，它测量角度的原理是 ．
【答案】对顶角相等
【详解】由题意得，对顶角量角器，它测量角度的原理是对顶角相等，
故答案为：对顶角相等．
40．（2022春•朝阳区校级期末）如图，连接直线外一点与直线上各点，，，，其中，这些线段，，，，中，最短的线段是 ．
【答案】
【详解】，
这些线段，，，，中，最短的线段是．
故答案为：．