初中数学北师大版九年级上册3 用公式法求解一元二次方程背景图课件ppt

这是一份初中数学北师大版九年级上册3 用公式法求解一元二次方程背景图课件ppt，共21页。PPT课件主要包含了课前预习，课前导入，典例讲练等内容，欢迎下载使用。
数学 九年级上册 BS版
运用公式法解决几何实际问题：解答与几何图形有关的应 用问题，应把握几何图形的面积，找出未知量与已知量间的内 在联系，根据相关公式列出方程，再通过解方程求出问题的解.注意：求得的解应符合题意和实际意义.
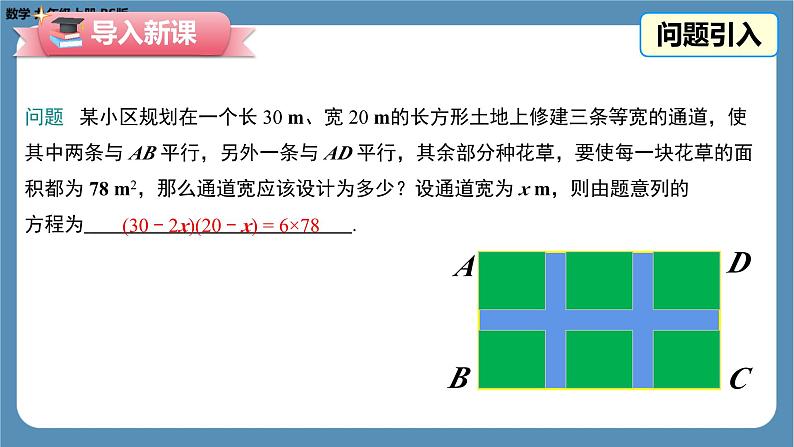
问题 某小区规划在一个长 30 m、宽 20 m的长方形土地上修建三条等宽的通道，使其中两条与 AB 平行，另外一条与 AD 平行，其余部分种花草，要使每一块花草的面积都为 78 m2，那么通道宽应该设计为多少？设通道宽为 x m，则由题意列的方程为 .
(30 - 2x)(20 - x) = 6×78
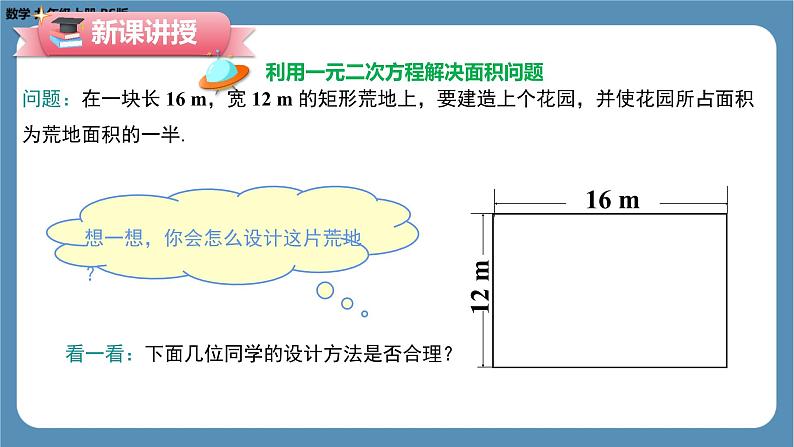
利用一元二次方程解决面积问题
问题：在一块长 16 m，宽 12 m 的矩形荒地上，要建造上个花园，并使花园所占面积为荒地面积的一半.
看一看：下面几位同学的设计方法是否合理？
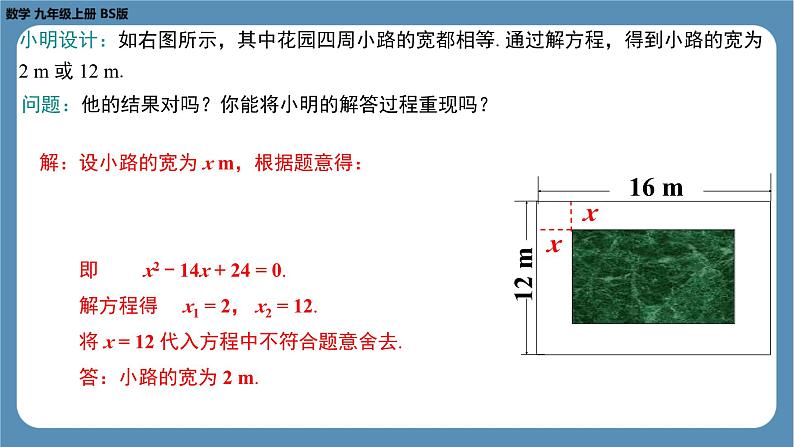
解：设小路的宽为 x m，根据题意得： 即 x2 - 14x + 24 = 0. 解方程得 x1 = 2， x2 = 12. 将 x = 12 代入方程中不符合题意舍去. 答：小路的宽为 2 m.
小明设计：如右图所示，其中花园四周小路的宽都相等.通过解方程，得到小路的宽为 2 m 或 12 m.
问题：他的结果对吗？你能将小明的解答过程重现吗？
解：由图片信息得，四个扇形组成一个圆设扇形半径为 x m，根据题意得： 即 πx2 = 96. 解方程得 x1 = (舍去)，x2 = . 答：扇形半径约为 5.5 m.
小亮设计： 如右图所示，其中花园每个角上的扇形都相同.
问题：你能帮小亮计算一下这个扇形的半径是多少吗？
解：设小路的宽为 x m，根据题意得： 即 x2 - 28x + 96 = 0. 解方程得 x1 = 4，x2 = 24. 将 x = 24 代入方程中不符合题意舍去.答：小路的宽为 4 m.
小颖设计：如右图所示，其中花园小路是两条互相垂直的矩形，且它的宽都相等.
问题：你能帮小颖计算一下图中小路的宽吗？
如图，从一块长80 cm、宽60 cm的铁片中间截去一个小矩形，使截去小矩形的面积是原来铁片面积的一半，并且剩下的方框四周的宽度一样，求这个宽度.设这个宽度为 x cm，则可列方程为 .
【点拨】列一元二次方程解决实际问题时，关键是理解题意，找出图中隐含的等量关系，利用等量关系列方程.解决本题的关键是通过“截去小矩形的面积是原来铁片面积的一半”得出等量关系.
1. 《九章算术》中有一题：“今有户高多于广六尺八寸，两隅相去适一丈.问户高、广各几何”.大意是：已知长方形门的高比宽多6尺8寸，门的对角线长1丈，那么门的高和宽各是多少？高是 尺，宽是 尺.（注：1尺＝10寸，1丈＝10尺）
解：设长方体木箱的宽为 x dm，则长为（ x ＋5）dm.根据题意， 得8 x （ x ＋5）＝528.整理，得 x2＋5 x －66＝0.
解得 x1＝6， x2＝－11（不合题意，舍去）.所以长方体木箱的长为11 dm，宽为6 dm.
2. 已知长方体木箱的高是8 dm，长比宽多5 dm，体积是528 dm3，求这个长方体木箱的长与宽.
如图，有一块长52 m、宽40 m的矩形场地，市政府准备在上面修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，且要使绿化面积为1 900 m2，求道路的宽度.
解：设道路的宽度为 x m.由题意，得（52－ x ）（40－ x ）＝1 900.整理，得 x2－92 x ＋180＝0.解得 x1＝2， x2＝90（不符合题意，舍去）.故道路的宽度为2 m.
【点拨】在与几何图形有关的应用题中，当数量关系不明显时，需要作适当的变换，再列方程解答.常见的解决此类问题的方法是将不规则的图形通过平移、分割或补全变成规则图形，使问题简单明了.注意：方程有多个解时，要舍去不符合题意的解.
为响应市委市政府提出的建设“绿色城市”的号召，某单位准备将院内一块长30 m、宽20 m的矩形空地建成一个矩形花园，要求在花园中修两条纵向平行和一条横向弯折的小道，剩余的地方种植花草.如图，要使种植花草的面积为532 m2 ，则小道进出口的宽度应为 m.（注：所有小道进出口的宽度相等，且每段小道均为平行四边形）
如图，利用一面墙（墙长25 m），用总长度为49 m的栅栏（图中实线部分）围成一个矩形围栏 ABCD ，且中间共留两个1 m宽的小门.设栅栏 BC 的长为 x m.
（1）若矩形围栏 ABCD 的面积为210 m2，求栅栏 BC 的长.
解：由 BC ＝ x m，得 AB ＝49＋1＋1－3 x ＝（51－3 x ）m.
（1）由题意，得 x （51－3 x ）＝210.整理，得 x2－17 x ＋70＝0.
解得 x1＝7， x2＝10.当 x ＝7时，51－3 x ＝51－3×7＝30＞25，不符合题意，舍去；当 x ＝10时，51－3 x ＝51－3×10＝21＜25，符合题意.所以栅栏 BC 的长为10 m.
（2）矩形围栏 ABCD 的面积能不能达到240 m2？若能，求出相应 x 的值；若不能，请说明理由.
（2）矩形围栏 ABCD 的面积不能达到240 m2.理由如下：由题意，得 x （51－3 x ）＝240.整理，得 x2－17 x ＋80＝0.因为Δ＝（－17）2－4×1×80＝－31＜0，所以原方程没有实数根.所以矩形围栏 ABCD 的面积不可能达到240 m2.
【点拨】判断方案是否能实现，需要满足两个条件：①一元二次方程有解；②一元二次方程的解符合实际且符合题意.
将一条长为40 cm的铁丝剪成两段，并将每一段铁丝围成一个正方形.（1）要使这两个正方形的面积之和为52 cm2 ，那么这条长铁丝剪成两段后的长度分别是多少？
（2）两个正方形的面积之和能等于48 cm2吗？若能，求出两段铁丝的长度；若不能，请说明理由.