高中数学人教A版 (2019)必修 第一册5.3 诱导公式精品练习题

这是一份高中数学人教A版 (2019)必修 第一册5.3 诱导公式精品练习题，文件包含专题53诱导公式原卷版docx、专题53诱导公式解析版docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

知识点一
公式一
知识点二
公式二
知识点三
公式三
知识点四
公式四
知识点五
公式五
知识点六
公式六
知识点七
综合结论
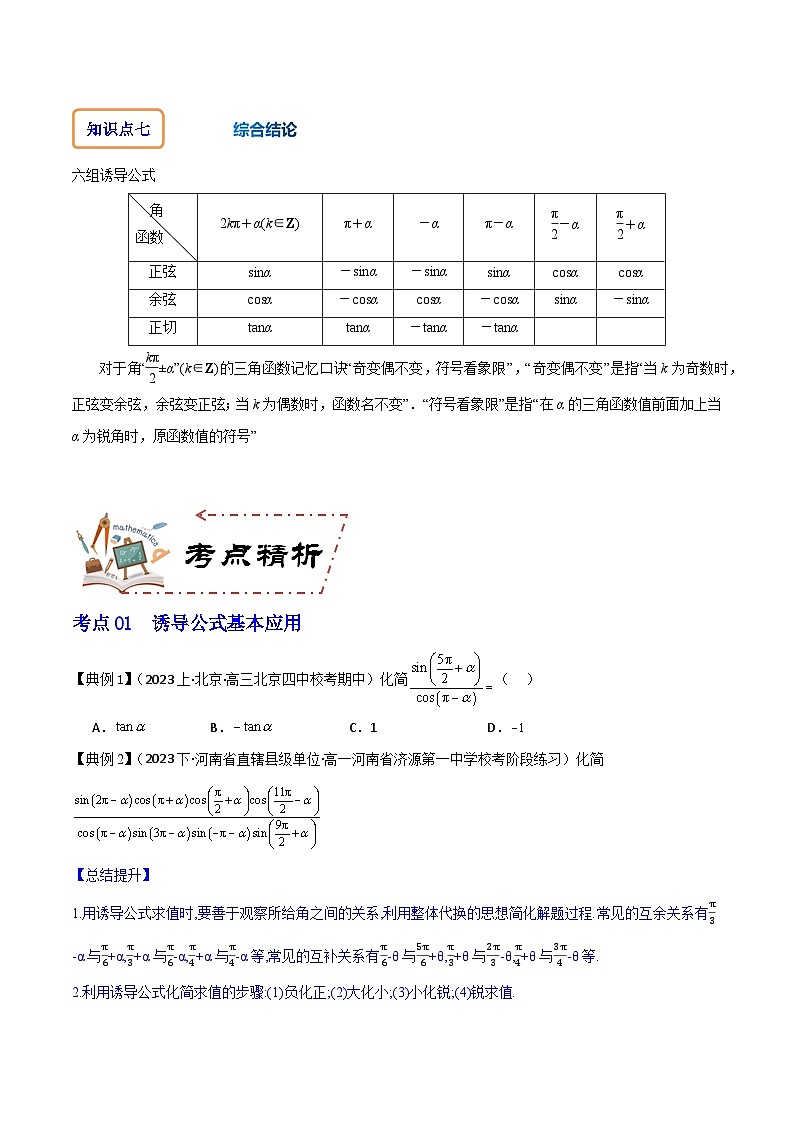
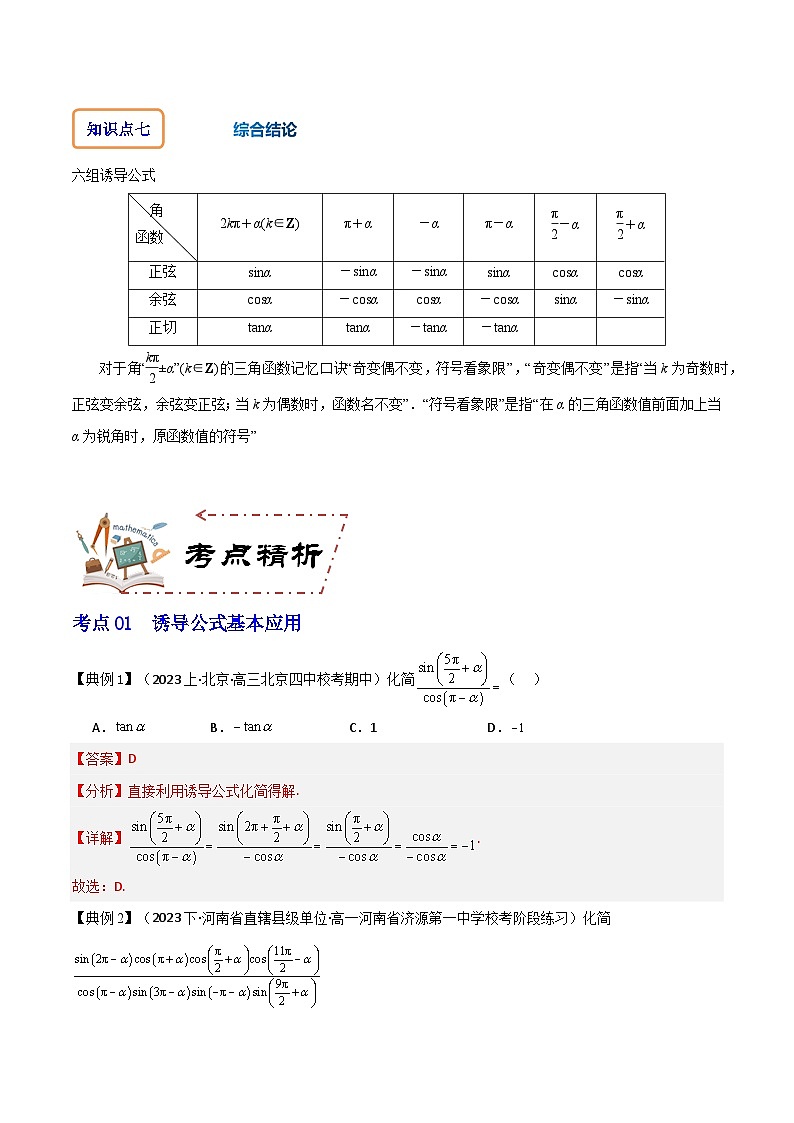
六组诱导公式
对于角“eq \f(kπ,2)±α”(k∈Z)的三角函数记忆口诀“奇变偶不变，符号看象限”，“奇变偶不变”是指“当k为奇数时，正弦变余弦，余弦变正弦；当k为偶数时，函数名不变”．“符号看象限”是指“在α的三角函数值前面加上当α为锐角时，原函数值的符号”
考点01 诱导公式基本应用
【典例1】（2023上·北京·高三北京四中校考期中）化简（ ）
A．B．C．1D．
【答案】D
【分析】直接利用诱导公式化简得解.
【详解】.
故选：D.
【典例2】（2023下·河南省直辖县级单位·高一河南省济源第一中学校考阶段练习）化简
【答案】
【分析】应用诱导公式化简后，根据同角三角函数的关系得解.
【详解】原式．
【总结提升】
1.用诱导公式求值时,要善于观察所给角之间的关系,利用整体代换的思想简化解题过程.常见的互余关系有π3-α与π6+α,π3+α与π6-α,π4+α与π4-α等,常见的互补关系有π6-θ与5π6+θ,π3+θ与2π3-θ,π4+θ与3π4-θ等.
2.利用诱导公式化简求值的步骤:(1)负化正;(2)大化小;(3)小化锐;(4)锐求值.
考点02 同角公式、诱导公式的综合应用
【典例3】（2022上·新疆乌鲁木齐·高一新疆农业大学附属中学校考期末）已知
(1)化简；
(2)若是第三象限角，且，求.
【答案】(1)
(2)
【分析】（1）利用诱导公式化简；
（2）由，可求得和，可得.
【详解】（1）.
（2）若是第三象限角，且，有
则，，
所以.
【典例4】（2022上·广东广州·高一广州市第九十七中学校考阶段练习）已知．
(1)化简,并求的值;
(2)若,且,求的值．
【答案】(1);
(2)
【分析】(1)先根据诱导公对进行化简,再将代入进算出结果即可;
(2)将代入可求,根据的正负及,可判断正负,从而判断正负,对平方再开方,代入即可得所求.
【详解】（1）解:由题知
,
;
（2）,,
,且,
,
故.
考点03 三角函数式化简、求值
【典例5】（2023上·江苏·高一专题练习）化简下列各式：
(1)；
(2)．
【答案】(1)1
(2)
【分析】利用诱导公式，化简求值.
【详解】（1）原式．
（2）原式
．
【典例6】（2022上·黑龙江佳木斯·高一校考期末）
(1)若为第二象限角，且，求的值.
(2)化简：.
【答案】(1)
(2)
【分析】（1）利用同角三角函数的基本关系求解；
（2）利用诱导公式进行化简.
【详解】（1）因为为第二象限角，所以，又，
所以，
所以.
（2）
.
【规律方法】
1.明确三角函数式化简的原则和方向
(1)切化弦，统一名．
(2)用诱导公式，统一角．
(3)用因式分解将式子变形，化为最简．
也就是：“统一名，统一角，同角名少为终了”．
2.化简要求:(1)化简过程是恒等变形;(2)结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值.
考点04 三角恒等式的证明
【典例7】（2021上·高一课时练习）（1）求证：；
（2）设，求证.
【答案】（1）证明见解析；（2）证明见解析.
【分析】（1）（2）应用诱导公式化简等式中结构复杂的一侧，即可证结论.
【详解】（1）左边= =右边，所以原等式成立.
（2）方法1：左边= ===右边，所以原等式成立.
方法2：由，得，
所以，等式左边= ===右边，等式成立.
【典例8】（2021·高一课时练习）证明：，．
【答案】证明见解析
【分析】按的奇偶性分类讨论，用诱导公式变形可证．
【详解】证明：当n为偶数时，令，，
左边．
右边，∴左边=右边．
当n为奇数时，令，，
左边
．
右边，∴左边=右边．
综上所述，，成立．
【规律方法】
1.三角恒等式的证明一般有三种方法：①一端化简等于另一端；②两端同时化简使之等于同一个式子；③作恒等式两端的差式使之为0．
2证明条件恒等式，一般有两种方法：一是在从被证等式一边推向另一边的适当时候将条件代入，推出被证等式的另一边，这种方法称作代入法；二是直接将条件等式变形，变形为被证的等式，这种方法称作推出法，证明条件等式时，不论使用哪一种方法，都要依据要证的目标的特征进行变形．
1.（2014·安徽·高考真题（理））设函数满足当时，，则（ ）
A．B．C．0D．
【答案】A
【解析】
【详解】
试题分析：由题意，
，故选A.
2.（2021·江苏·高考真题）已知，且，则的值是_________.
【答案】
【分析】
先用诱导公式化简，再通过同角三角函数的基本关系求得.
【详解】
，因为，所以，所以，所以，所以.
故答案为：.
3.（2016·全国·高考真题（文））已知θ是第四象限角，且sin（θ+）=，则tan（θ–）=___________.
【答案】
【解析】
【分析】
由题求得θ的范围，结合已知求得cs（θ），再由诱导公式求得sin（）及cs（），进一步由诱导公式及同角三角函数基本关系式求得tan（θ）的值．
【详解】
解：∵θ是第四象限角，
∴，则，
又sin（θ），
∴cs（θ）．
∴cs（）＝sin（θ），sin（）＝cs（θ）．
则tan（θ）＝﹣tan（）．
故答案为．
一、单选题
1.（2021下·高一课时练习）若，则属于第__________象限角.
A．一B．二C．三D．四
【答案】C
【分析】先利用诱导公式和同角三角函数的关系对化简，得，从而可得，进而可求得答案
【详解】解：由，得
，
，
所以，
所以，所以属于第三象限的角，
故选：C
2．（2023上·江苏扬州·高三统考期中）已知，则（ ）.
A．B．C．1D．3
【答案】A
【分析】利用诱导公式以及同角三角函数之间的基本关系化简代入计算可得结果为.
【详解】由诱导公式可得，
将代入计算可得，原式.
故选：A
3．（2023上·安徽·高三校联考期中）已知角的顶点在坐标原点，始边与轴的非负半轴重合，终边经过点，则（ ）
A．B．C．0D．
【答案】C
【分析】根据终边上的点可求得：，，再结合三角函数诱导公式从而求解.
【详解】因为：（为坐标原点），
所以:由三角函数的定义，得，，
所以：.故C项正确.
故选：C.
4．（2023上·陕西西安·高三校考阶段练习）已知，则等于（ ）
A．1B．－C．D．－
【答案】D
【分析】利用三角诱导公式以及同角三角函数的基本关系求解.
【详解】因为，
所以，
又因为，
故选:D.
二、填空题
5．（2022上·四川遂宁·高一校考期末）已知，则 .
【答案】/
【分析】利用三角函数的诱导公式求解.
【详解】,
故答案为：.
6．（2022上·湖南长沙·高一雅礼中学校考阶段练习）若、是关于的方程的两个根，则 .
【答案】/
【分析】先根据韦达定理得到，进而求得，，再结合诱导公式化简求值即可.
【详解】由题意得，，则或，
又，即，解得或（舍去），
则，
所以
.
故答案为：.
7.（2022上·湖北孝感·高一校考期末）已知，且，则 ； .
【答案】
【分析】利用同角三角函数的基本关系可求得的值，再结合诱导公式即可得解.
【详解】因为，所以，
因为，所以，
所以，
.
故答案为：；.
三、解答题
8．（2023上·浙江·高一校联考阶段练习）在平面直角坐标系中，角以轴的非负半轴为始边，它的终边与单位圆交于第二象限内的点.
(1)若，求及的值；
(2)若，求点的坐标.
【答案】(1)；
(2)
【分析】（1）根据三角函数的定义式，结合同角三角函数关系式及诱导公式化简可得解；
（2）根据三角函数定义式列方程，解方程.
【详解】（1）由已知角的终边与单位圆交于第二象限内的点，
则，，，，且，
由，得，
则，
再由诱导公式可得
（2）由，得，，
又，则，解得，
所以，
所以，
所以，，
即.
9．（2023下·北京·高一中关村中学校考期中）已知函数
(1)求的定义域；
(2)若，且，求的值.
【答案】(1)
(2)
【分析】（1）根据，，解得函数的定义域为.
（2）化简，代入求得
然后根据以及同角三角函数间的关系，解得，
最后化简解得：
【详解】（1）依题意，，.
所以有.
所以函数的定义域为.
（2）.
由，得.
又因为，
所以.
所以.
所以
10．（2023上·江苏苏州·高一校考阶段练习）已知．
(1)求的值；
(2)若，且角的终边与角关于x轴对称，求的值．
【答案】(1)
(2)
【分析】（1）根据题意结合齐次式问题分析求解；
（2）根据对称性可得，结合齐次式问题分析求解.
【详解】（1）原式
，
即.
（2）因为，且，可知，
则，，
所以
11．（2023·高一单元测试）已知为第三象限角，且．
(1)化简并求；
(2)若，求的值．
【答案】(1)，
(2)
【分析】（1）利用诱导公式化简求得，再代入求值；
（2）先根据诱导公式求得的值，然后根据同角之间的关系求出的值，即可求解.
【详解】（1），
（2）因为，所以，
又因为是第三象限角，所以，
所以.
12．（2021·高一课前预习）求证：＝．
【答案】证明见解析
【分析】运用诱导公式结合同角三角函数的基本关系将等式两边分别化简，进而证明问题.
【详解】左边
.
右边.
∴左边＝右边，故原等式成立．
角
函数
2kπ＋α(k∈Z)
π＋α
－α
π－α
eq \f(π,2)－α
eq \f(π,2)＋α
正弦
sinα
－sinα
－sinα
sinα
csα
csα
余弦
csα
－csα
csα
－csα
sinα
－sinα
正切
tanα
tanα
－tanα
－tanα