数学13.3 全等三角形的判定集体备课ppt课件

这是一份数学13.3 全等三角形的判定集体备课ppt课件，共29页。PPT课件主要包含了①ABDE，②BCEF，③CAFD，④∠A∠D，⑤∠B∠E，⑥∠C∠F，知识点，不全等，几何语言，先找隐含条件等内容，欢迎下载使用。

1. 探索三角形全等的条件；2. 探索并掌握判定两个三角形全等的“边边边”判定方法，会用“边边边”证明两个三角形全等并解决简单问题.3. 理解三角形的稳定性.
1. 什么叫全等三角形？
能够完全重合的两个三角形叫做全等三角形.
2. 全等三角形有什么性质？
全等三角形的对应边相等，对应角相等.
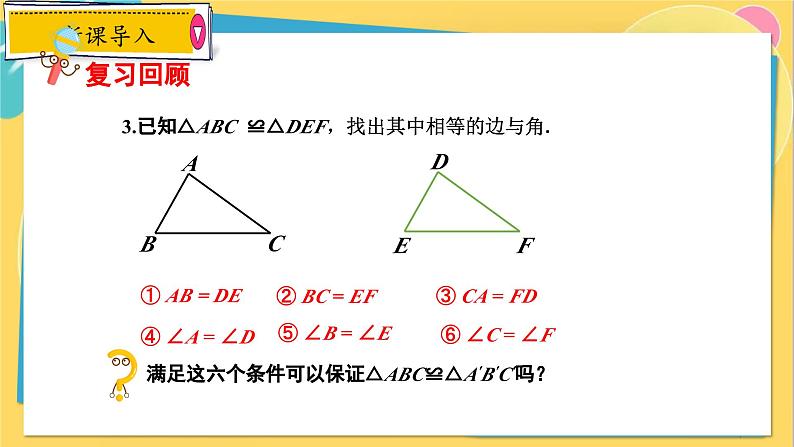
3.已知△ABC ≌△DEF，找出其中相等的边与角.
　满足这六个条件可以保证△ABC≌△A′B′C′吗？
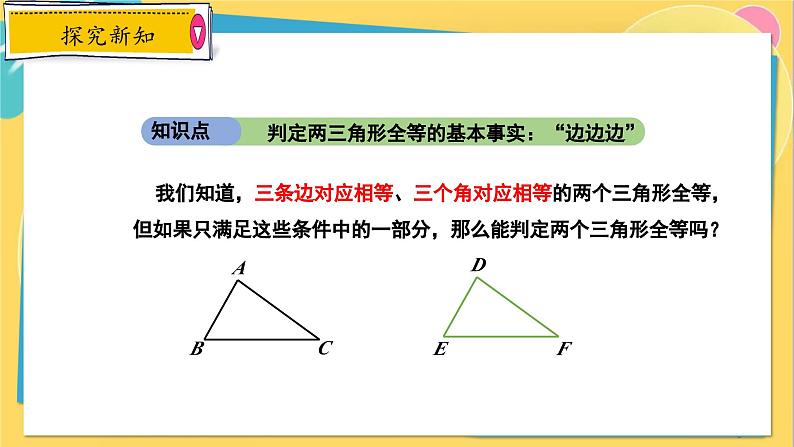
判定两三角形全等的基本事实：“边边边”
　我们知道，三条边对应相等、三个角对应相等的两个三角形全等，但如果只满足这些条件中的一部分，那么能判定两个三角形全等吗？
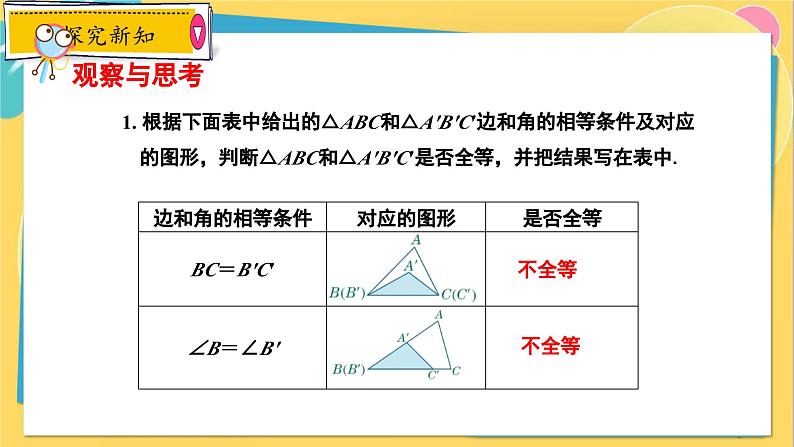
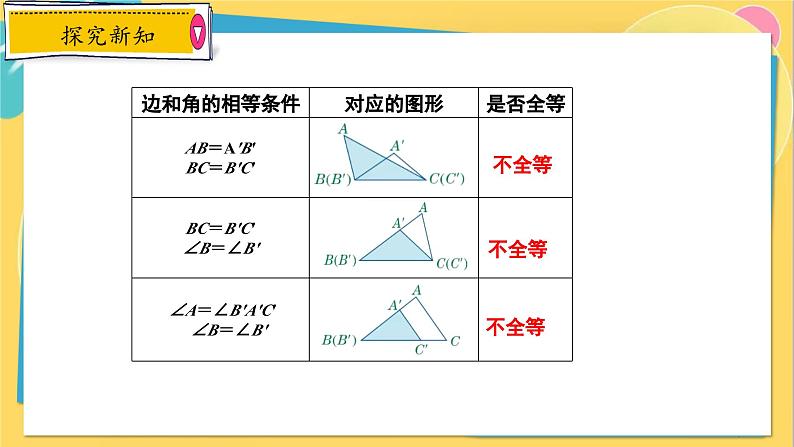
1. 根据下面表中给出的△ABC和△A′B′C′边和角的相等条件及对应的图形，判断△ABC和△A′B′C′是否全等，并把结果写在表中.
总结：1.当两个三角形只有一条边或一个角对应相等时，两个三角形不一定全等.2.当两个三角形只有两条边或两个角或一边一角对应相等时，两个三角形不一定全等.
2.有三个角对应相等的两个三角形一定全等吗? 说说你的理由.
3. 小亮认为，判断两个三角形全等的较少条件，只有以下三种情况才有可能：三条边对应相等，或两条边和一个角分别对应相等，或两个角和一条边分别对应相等.你认为这种说法对吗?
当三个内角对应相等时，两个三角形不一定全等.
准备一些长都是13 cm的细铁丝. (1)和同学一起，每人用一根铁丝，折成一个边长分别是 3 cm，4 cm，6 cm的三角形. 把你做出的三角形和同学做出的三角形进行比较，它们能重合吗?
(2)和同学一起，每人用一根铁丝，余下 1 cm，用其余部分折成边长分别是3 cm，4 cm，5 cm的三角形. 再和同学做出的三角形进行比较，它们能重合吗?
(3)每人用一根铁丝，任取一组能够构成三角形的三边长的数据，和同桌分别按这些数据折三角形，折成的两个三角形能重合吗?
文字语言：如果两个三角形的三边对应相等，那么这两个三角形全等，简记为“边边边”或“SSS”.
在△ABC 和△A′B′C′ 中，
∴△ABC≌△A′B′C′(SSS).
如图，已知点A，D，B，F在同一条直线上，AC＝FE，BC＝DE，AD＝FB.求证：△ABC≌△FDE.
AC＝FE、BC＝DE
证明三角形全等的书写步骤：
① 准备条件：证全等时要用的条件要先证好；
② 指明范围：写出在哪两个三角形中；
③ 摆齐条件：摆出三个条件用大括号括起来；
④ 写出结论：写出全等结论.
已知：如图，AB＝AC，BD＝CD．求证：△ABD≌△ACD.
证明：在△ABD和△ACD中，∵∴△ABD≌△CBD(SSS)．
全等三角形判定“边边边”的简单应用
如图，已知：AB＝AC，AD＝AE，BD＝CE.求证：∠BAC＝∠DAE.
导引：要证明∠BAC＝∠DAE，而这两个角所在的三角形显然不全等，我们可以利用等式的性质将其转化为证明∠BAD＝∠CAE；由已知的三组相等线段可证明△ABD≌△ACE，根据全等三角形的性质可得∠BAD＝∠CAE.
1.如图是一个风筝模型的框架，由DE＝DF，EH＝FH，就能说明∠DEH＝∠DFH.试用你所学的知识说明理由．
2. 如图，已知AE＝AD，AB＝AC，EC＝DB，下列结论：①∠C＝∠B；②∠D＝∠E；③∠EAD＝∠BAC；④∠B＝∠E.其中错误的是(　　)A．①② B．②③ C．③④ D．只有④
　　运用“SSS”证明两个三角形全等主要就是找边相等，边相等除了已知边相等以外，还有以下几种方式：①中点；②公共边；③一部分相等，另一部分是公共的．
1.用三根木条钉成一个三角形框架(如图)，拉动它，观察它的外形是否发生变化.
无论怎样拉动，三角形的形状和大小都不改变，即只要三角形的三边确定，它的形状和大小就完全确定，三角形所具有的这种性质叫做“三角形的稳定性”.
2.用四根木条钉成一个四边形形框架(如图)，拉动它，观察它的外形是否发生变化.
总结：三角形具有稳定性，四边形不具有稳定性.
如图，自行车的车身为三角结构，这是因为三角形具有(　　)A.对称性B.稳定性C.全等性D.以上都不是
分析：根据三角形具有稳定性进行解答即可.
已知：∠AOB．求作∠A′O′B′=∠AOB．
作法： (1)以点O 为圆心，任意长为半径画弧，分别交OA，OB 于点C、D；
(2)画一条射线O′A′，以点O′为圆心，OC 长为半径画弧，交O′A′于C′；
(3)以点C′为圆心，CD 长为半径画弧，与第(2)步中所画的弧交于D′；
(4)过点D′画射线O′B′，则∠A′O′B′=∠AOB．
1. 如图，已知 AB ＝ AC ， AE ＝ AD ，点 B ， D ， E ， C 在 同一条直线上，要利用“SSS”推理得出△ ABE ≌△ ACD ，还需要添加的一个条件可以是(　B　)
2. 如图，在△ ABC 中， AB ＝ AC ， BE ＝ CE ，则直接由 “SSS”可以判定(　C　)
3. 如图， C 是 BD 的中点， AB ＝ ED ， AC ＝ EC . 求证：△ ABC ≌△ EDC .