




专题04 图形的相似(考点清单,11个考点)-九年级上学期数学期末考点大串讲(北师大版)
展开【考点1】比例性质 【考点2】比例线段
【考点3】平行线分线段成比例定理及其推论基本应用
【考点4】相似多边形的性质 【考点5】 相似三角形的概念
【考点6】相似三角形的判定 【考点7 】相似三角形的性质
【考点8 】相似三角形的判定和性质综合【考点9 】相似三角形的应用综合
【考点10 】图形的位似 【考点11 】作图-位似
【考点1】比例性质
1.已知,则的值为( )
A.5B.﹣5C.D.
【答案】B
【解答】解:∵,
∴p=q,
∴===﹣5.
故选:B.
2.已知5x=3y(xy≠0),那么下列比例式中成立的是( )
A.B.C.D.
【答案】B
【解答】解:A、∵=,
∴3x=5y,
故A不符合题意;
B、∵=,
∴5x=3y,
故B符合题意;
C、∵=,
∴3x=5y,
故C不符合题意;
D、∵=,
∴xy=15,
故D不符合题意;
故选:B.
3.,则的值为( )
A.B.C.﹣2D.2
【答案】D
【解答】解:∵,
∴a+2b=4a,
∴b=a,
∴==2.
故选:D.
4.若,则的值为( )
A.B.C.D.
【答案】C
【解答】解:∵=,
∴设a=3k,b=5k,
则===.
故选:C.
【考点2】比例线段
5.下列各组线段中是成比例线段的是( )
A.1cm,2cm,3cm,4cmB.1cm,2cm,2cm,4cm
C.3cm,5cm,9cm,13cmD.1cm,2cm,2cm,3cm
【答案】B
【解答】解:∵1×4≠2×3,
∴选项A不成比例;
∵1×4=2×2,
∴选项B成比例;
∵3×13≠5×9,
∴选项C不成比例;
∵3×1≠2×2,
∴选项D不成比例
故选:B.
6.已知线段a、b、c,当a=4,b=5时,则a、b的比例中项c等于( )
A.B.C.±6D.6
【答案】B
【解答】解:根据比例中项的概念,得c2=ab=20,
所以c=±2,
又线段不能是负数,﹣2应舍去,
所以c=2.
故选:B.
7.已知线段a,b,c,其中c是a,b的比例中项,若a=3cm,b=27cm,则线段c的长为( )
A.81cmB.9cmC.﹣9cmD.±9cm
【答案】B
【解答】解:∵c是a、b的比例中项,
∴c2=ab,
∵a=3cm,b=27cm,
∴c2=81,
∵c>0,
∴c=9cm.
故选:B.
8.若,则的值为( )
A.B.C.D.1
【答案】B
【解答】解:∵,
∴b=3a,d=3c,
∴=,
故选:B.
9.已知四个数2,﹣3,4,x成比例,则x的值是( )
A.6B.﹣6C.D.﹣
【答案】B
【解答】解:由题意得,2:(﹣3)=4:x,
∴2x=﹣12,
∴x=﹣6.
故选:B.
【考点3】平行线分线段成比例定理及其推论基本应用
10.已知直线DE分别交△ABC边AB、AC于D、E点,那么不能推出DE∥BC的是( )
A.B.C.D.
【答案】C
【解答】解:∵,
∴△ADE∽△ABC,
∴∠B=∠ADE,
∴DE∥BC,故A不符合题意;
∵,
∴,
∴DE∥BC,故B不符合题意;
由不能推得DE∥BC,故C符合题意;
∵,
∴,
∴,即.
∴DE∥BC,故D不符合题意.
故选:C.
11.如图,AD∥BE∥CF,点B,E分别在AC,DF上,,EF=6,DF的长( )
A.3B.4C.5D.10
【答案】D
【解答】解:∵AD∥BE∥CF,
∴=,即=,
∴DE=4,
∴DF=DE+EF=4+6=10.
故选:D.
12.如图,AD∥BE∥CF,若DE=7,DF=21,AB=6,则AC的长度是( )
A.12B.18C.15D.
【答案】B
【解答】解:∵AD∥BE∥CF,
∴=,
∴=,
∴AC=18.
故选:B.
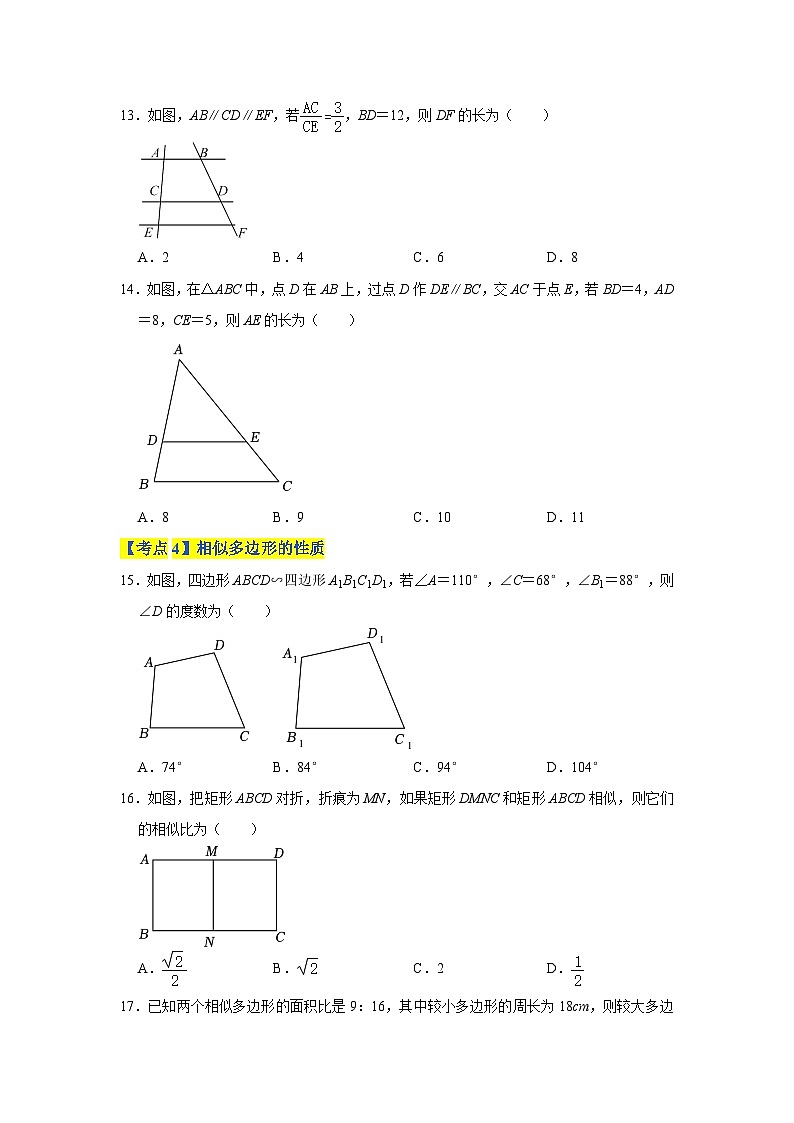
13.如图,AB∥CD∥EF,若,BD=12,则DF的长为( )
A.2B.4C.6D.8
【答案】D
【解答】解:∵AB∥CD∥EF,
∴,
∵,BD=12,
∴,
解得:DF=8,
故选:D.
14.如图,在△ABC中,点D在AB上,过点D作DE∥BC,交AC于点E,若BD=4,AD=8,CE=5,则AE的长为( )
A.8B.9C.10D.11
【答案】C
【解答】解:∵DE∥BC,
∴AD:DB=AE:EC,
∵BD=4,AD=8,CE=5,
∴8:4=AE:5,
∴AE=10.
故选:C.
【考点4】相似多边形的性质
15.如图,四边形ABCD∽四边形A1B1C1D1,若∠A=110°,∠C=68°,∠B1=88°,则∠D的度数为( )
A.74°B.84°C.94°D.104°
【答案】C
【解答】解:∵四边形ABCD∽四边形A1B1C1D1,∠B1=88°,
∴∠B=∠B1=88°.
∵四边形ABCD的内角和为(4﹣2)×180°=360°,∠A=110°,∠C=68°,
∴∠D=360°﹣∠A﹣∠B﹣∠C=360°﹣110°﹣88°﹣68°=94°.
故选:C.
16.如图,把矩形ABCD对折,折痕为MN,如果矩形DMNC和矩形ABCD相似,则它们的相似比为( )
A.B.C.2D.
【答案】A
【解答】解:设矩形ABCD的长AD=x,宽AB=y,
则DM=AD=x,
∵矩形DMNC与矩形ABCD相似,
∴,即 ,
即y2=x2.
∴y:x=1:=.
故选:A.
17.已知两个相似多边形的面积比是9:16,其中较小多边形的周长为18cm,则较大多边形的周长为( )
A.24cmB.27cmC.28cmD.32cm
【答案】A
【解答】解:两个相似多边形的面积比是9:16,
∴两个相似多边形的相似比是3:4,
∴两个相似多边形的周长比是3:4,
设较大多边形的周长为为xcm,
由题意得,18:x=3:4,
解得,x=24,
故选:A.
18.两个相似五边形,一组对应边的长分别为4cm和6cm,若它们的面积之和为260cm2,则较大五边形的面积是( )
A.100cm2B.180cm2C.75cm2D.30cm2
【答案】B
【解答】解:∵两个相似五边形的一组对应边的长分别是4cm,6cm,
∴这两个相似五边形的相似比为2:3,
设较大的五边形的面积为x cm2,依据它们的面积之和为260cm2,
∴m+m=260,
解得x=180,
即较大的五边形的面积为180cm2.
故选:B.
19.如图,将一个矩形纸片ABCD沿AD、BC的中点E、F的连线对折,要使对折后的矩形AEFB与原矩形ABCD相似,则原矩形ABCD的长AD和宽DC的比应为( )
A.2:1B.:1C.:1D.1:1
【答案】C
【解答】解:∵四边形ABCD是矩形,
∴AB=CD,
∵点E是AD的中点,
∴AE=AD,
∵矩形AEFB与原矩形ABCD相似,
∴=,
∴=,
∴AD2=CD2,
∴AD2=2CD2,
∴AD:CD=:1,
故选:C.
【考点5】 相似三角形的概念
20.如图,在三角形纸片ABC中,AB=9,AC=6,BC=12,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A.B.
C.D.
【答案】B
【解答】解:在三角形纸片ABC中,AB=9,AC=6,BC=12,
A.因为,对应边,,
所以沿虚线剪下的涂色部分的三角形与△ABC不相似,
故此选项不符合题意;
B.因为,对应边,又∠A=∠A,
所以沿虚线剪下的涂色部分的三角形与△ABC相似,
故此选项符合题意;
C.因为,对应边,
即:,
所以沿虚线剪下的涂色部分的三角形与△ABC不相似,
故此选项不符合题意;
D.因为,对应边,,
所以沿虚线剪下的涂色部分的三角形与△ABC不相似,
故此选项不符合题意;
故选:B.
21.给出下列四个命题:
(1)等腰三角形都是相似三角形;
(2)直角三角形都是相似三角形;
(3)等腰直角三角形都是相似三角形;
(4)等边三角形都是相似三角形.其中真命题有( )
A.1个B.2个C.3个D.4个
【答案】B
【解答】解:(3)(4)正确,
(3)符合两组对应边的比相等且相应的夹角相等的两个三角形相似;
(4)符合三组对应边的比相等的两个三角形相似.
而(1)(2)不满足判定三角形相似的条件.
故选:B.
【考点6】相似三角形的判定
22.如图,在△AOB和△COD中,已知∠AOC=∠BOD,则添加下列条件能判定△AOB和△COD相似的是( )
A.∠A=∠DB.∠B=∠BOCC.D.
【答案】A
【解答】解:∵∠AOC=∠BOD,
∴∠AOB=∠COD.
A、∠A=∠D,对应的两角相等,可以证明,符合题意;
B、∠B=∠BOC,不是对应角,不可以证明,不符合题意;
C、,不是对应边成比例,不可以证明,不符合题意;
D、,不是夹角的对应边成比例,不可以证明,不符合题意.
故选:A.
23.如图,已知D是△ABC的边AC上一点,根据下列条件,不能判定△CAB∽△CBD的是( )
A.∠A=∠CBDB.∠CBA=∠CDB
C.AB•CD=BD•BCD.BC2=AC•CD
【答案】C
【解答】解:∵∠C是公共角,
∴再加上∠A=∠CBD或∠CBA=∠CDB都可以证明△CAB∽△CBD,故A,B不符合题意,
C选项中的对两边成比例,但不是相应的夹角相等,所以选项C符合题意.
∵∠C=∠C,
若再添加,即BC2=AC⋅CD,可证明△CAB∽△CBD,故D不符合题意.
故选:C.
24.如图,AB=AC,作△ADC,使得点B,D在AC异侧,且AD=CD,∠ADC=∠BAC,E是BC延长线上一点,连接AB交CD于点F.求证:△ABC∽△DAC.
【答案】证明见解析.
【解答】证明:∵AB=AC,AD=CD,
∴,
∵∠BAC=∠ADC,
∴△ABC∽△DAC.
25.如图,已知AD•AC=AB•AE,∠DAE=∠BAC.求证:△DAB∽△EAC.
【答案】证明过程请看解答.
【解答】证明:∵AD•AC=AB•AE,
∴=,
∵∠DAE=∠BAC.
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠DAB=∠EAC,
∴△DAB∽△EAC.
26.如图,D是AC上一点,DE∥AB,∠B=∠DAE.
求证:△ABC∽△DAE.
【答案】见试题解答内容
【解答】证明:∵DE∥AB,
∴∠EDA=∠CAB,
又∵∠B=∠DAE,
∴△ABC∽△DAE.
27.如图8,在正方形ABCD中,点P是BC边上一点(不与点B,C重合),且AP⊥PE,PE交边DC于点E.
(1)求证:①△ABP∽△PCE;②CE•AB=PC•BP;
(2)若AP=2PE,求证:△APE∽△PCE.
【答案】(1)①证明见解答过程;②证明见解答过程;
(2)证明见解答过程.
【解答】证明:(1)①∵四边形ABCD是正方形,
∴AB=BC,∠B=∠PCD=90°,
∴∠PAB+∠APB=90°,
∵AP⊥PE,
∴∠APE=90°,
∴∠EPC+∠APB=90°.
∴∠PAB=∠EPC,
∴△ABP∽△PCE;
②∵△ABP∽△PCE,
∴=,
∴CE•AB=PC•BP;
(2)∵△ABP∽△PCE,
∴==,
∵AP=2PE,
∴AB=2PC,BP=2CE,
∵AB=BC,
∴BP=PC=2CE,
∴=,
又∠APE=∠C=90°,
∴△APE∽△PCE.
28.在△ABC中,AF⊥BC,CE⊥AB,垂足分别是F,E,连接EF.求证:
(1)△BAF∽△BCE;
(2)△BEF∽△BCA.
【答案】(1)(2)证明见解析.
【解答】证明:(1)∵AF⊥BC,CE⊥AB,
∴∠AFB=∠CEB=90°.
∵∠B=∠B,
∴△BAF∽△BCE.
(2)∵△BAF∽△BCE,
∴=,
∵∠B=∠B,
∴△BEF∽△BCA.
【考点7 】相似三角形的性质
29.若两个相似三角形周长的比为1:4,则这两个三角形对应边的比是( )
A.1:2B.1:4C.1:8D.1:16
【答案】B
【解答】解:∵两个相似三角形周长的比为1:4,
∴这两个三角形对应边的比为1:4,
故选:B.
30.若两个相似三角形对应边上的高的比为4:9,则这两个三角形的周长的比为( )
A.2:3B.4:9C.16:81D.不能确定
【答案】B
【解答】解:∵两个相似三角形对应边上的高的比为4:9,
∴这两个三角形的相似比为4:9,
∴两个相似三角形的周长比为4:9;
故选:B.
31.已知△ADE与△ABC相似,且周长比为1:3,则△ADE与△ABC的面积比为( )
A.1:1B.1:3C.1:6D.1:9
【答案】D
【解答】解:由题意可知△ADE与△ABC相似,且周长比为1:3,△ABC与△ADE的面积比为相似比的平方,故为1:9.
故选:D.
32.两个相似三角形的面积之比为1:4,较小的三角形的周长为4,则另一个三角形的周长为( )
A.16B.8C.2D.1
【答案】B
【解答】解:设另一个三角形的周长为x,则
4:x=,
解得:x=8.
故另一个三角形的周长为8,
故选:B.
33.如图,△ABC∽△ADE,S△ABC:S四边形BDEC=1:2,其中,DE的长为( )
A.B.C.D.6
【答案】A
【解答】解:∵S△ABC:S四边形BDEC=1:2,
∴S△ABC:S△ADE=1:3,
∵△ABC∽△ADE,
∴=,
∵CB=,
∴DE=.
故选:A.
34.如图,在矩形ABCD中,AB=9,BC=15,P,Q分别是BC,CD上的点,CQ=4,若△ABP与△PCQ相似,则BP的长为( )
A.3或B.3或12
C.3、12或D.3、12或
【答案】D
【解答】解:在矩形ABCD中,∠B=∠C=90°,AB=CD=9,BC=AD=15,
∵△ABP与△PCQ相似,
∴分△ABP∽△PCQ与△ABP∽△QCP两种情况求解:
①当△ABP∽△PCQ时,设BP=x,则PC=15﹣x,
∴,即,
解得:x=3或x=12,
②当△ABP∽△QCP时,设BP=x,则PC=15﹣x,
∴,即,
解得:,
综上所述,BP的长为3或12或.
故选:D.
【考点8 】相似三角形的判定和性质综合
35.如图,在平行四边形ABCD中,延长AD至点E,使DE=AD,连接BE交CD于点F.
(1)求证:△ABE∽△CFB;
(2)若CF=2,求AB的长.
【答案】(1)证明见解答;
(2)AB的长是3.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠E=∠CBF,
∵∠A=∠C,
∴△ABE∽△CFB.
(2)解:∵DE=AD,AD=CB,
∴DE=CB,
∵DE∥CB,
∴△DEF∽△CBF,
∴==,
∴DF=CF=×2=1,
∴AB=CD=CF+DF=2+1=3,
∴AB的长是3.
36.如图,在Rt△ABC中,∠ACB=90°,矩形DEFG的顶点D,E在边AB上,顶点G,F分别在边AC,BC上.
(1)求证:;
(2)若AD=GD,求△ADG与△FEB面积的比值.
【答案】(1)证明见解析;(2)9:4.
【解答】(1)证明:在矩形DEFG中,∠GDE=∠FED=90°,
∴∠GDA=∠FEB=90°,
∵∠C=∠GDA=90°,
∴∠A+∠AGD=∠A+∠B=90°,
∴∠AGD=∠B,
在△ADG和△FEB中,
∵∠AGD=∠B,∠GDA=∠FEB=90°,
∴△ADG∽△FEB,
∴=;
(2)解:∵四边形DEFG为矩形,
∴GD=EF,
∵△ADG∽△FEB,
∴=()2=()2=.
故答案为:9:4.
37.如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高.
(1)求证:△ADC∽△ACB;
(2)若AC=3,AB=4,求AD的长.
【答案】(1)见解析;(2).
【解答】(1)证明:∵CD⊥AB,
∴∠ADC=∠ADB=90°,
∵∠A=∠A,
∴△ADC∽△ACB;
(2)解:∵△ADC∽△ACB
∴,
即,
∴AD=.
38.如图,点E是矩形ABCD的边AB上一点,沿直线CE将△CBE翻折,使得点B落在AD边上,记作点F.
(1)求证:△AEF∽△DFC;
(2)若,且CD=10,求BC的长.
【答案】(1)证明见解答;
(2)14.5.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=∠D=90°,
∴∠CFD+∠DCF=90°,
由折叠得:∠EFC=∠B=90°,
∴∠AFE+∠CFD=90°,
∴∠AFE=∠DCF,
∴△AEF∽△DFC;
(2)解:∵△AEF∽△DFC,
∴==,
∵,且CD=10,
∴=,
∴AF=4,
由折叠得:BE=EF,
设BE=x,则AE=10﹣x,EF=BE=x,
由勾股定理得:AE2+AF2=EF2,
∴42+(10﹣x)2=x2,
∴x=5.8,
∴AE=10﹣5.8=4.2,
∴=,
∴DF=10.5,
∴BC=AF+DF=4+10.5=14.5.
39.如图,AC、BD交于点E,BC=CD,且BD平分∠ABC.
(1)求证:△AEB∽△CED;
(2)若BC=12,EC=6,AE=4,求AB的长.
【答案】(1)见解析;(2)8.
【解答】(1)证明:∵BC=CD,
∴∠D=∠CBD,
∵BD平分∠ABC,
∴∠CBD=∠DBA=∠D,
又∵∠AEB=∠CED,
∴△AEB∽△CED;
(2)解:∵△AEB∽△CED,
∴,
又∵BC=CD,
∴,
即,
∴AB=8.
【考点9 】相似三角形的应用综合
40.如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点A,镜子O,树底B三点在同一水平线上,眼睛与地面的高度为1.6米,OA=2.4米,OB=6米,则树高为( )米.
A.4B.5C.6D.7
【答案】A
【解答】解:点O作镜面的法线FO,由入射角等于反射角可知∠COF=∠DOF,
∵∠COA=90°﹣∠COF,
∠DOB=90°﹣∠DOF,
∴∠COA=∠DOB,
又∵∠CAO=∠OBD=90°,
∴△ACO∽△BDO,
∴=,
∵AC=1.6米,OA=2.4米,OB=6米,
∴=,
∴BD=4米,
答:树高为4米,
故选:A.
41.如图,小明同学利用相似三角形测量旗杆的高度,若测得木杆AB长2m,它的影长BC为1m,旗杆DE的影长EF为6m,则旗杆DE的高度为( )
A.9mB.10mC.11mD.12m
【答案】D
【解答】解:∵同一时刻物高与影长成正比,
∴=,
∵AB=2m,BC=1m,EF=6m,
∴=,
∴DE=12(m),
故选:D.
42.如图,某人拿着一把分度值为厘米的刻度尺,站在距电线杆30m的地方,手臂向前伸直,将刻度尺竖直,看到刻度尺上7cm的长度恰好遮住电线杆.已知臂长为70cm,则电线杆的高是( )
A.3mB.4mC.5mD.6m
【答案】A
【解答】解:作AN⊥EF于N,交BC于M,
∵BC∥EF,
∴AM⊥BC,
∴△ABC∽△AEF,
∴=,
∵AM=0.7m,AN=30m,BC=0.07m,
∴EF===3(m).
故选:A.
43.如图,我校小辰同学在学习完《利用相似三角形测高》后,利用标杆FC测量学校教学楼的高度.若标杆FC=2.5米,小辰同学眼高离地面AB=1.5米测得DC=23米,BC=1米,请你帮他求出学校体育馆ED的高度.
【答案】学校体育馆ED的高度是25.5米.
【解答】解:作AH⊥ED交FC于点G,如图所示:
∵FC⊥BD,ED⊥BD,AH⊥ED交FC于点G,
∴FG∥EH,
∵AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC,
∴AH=BD,AG=BC,
∵AB=1.5米,FC=2.5米,DC=23米,BC=1米,
∴FG=2.5﹣1.5=1(米),BD=24米,
∵FG∥EH,
∴,,
解得:EH=24米,
∴ED=24+1.5=25.5(米),
答:学校体育馆ED的高度是25.5米.
44.小明家窗外有一个路灯,每天晚上灯光都会透过窗户照进房间里,小明利用相关数学知识测量了这个路灯的高.如图,路灯顶部A处发光,光线透过窗子BC照亮地面的长度为DE,小明测得窗户距离地面高度BF=0.6m,窗高BC=1.4m,某一时刻,FD=0.6m,DE=2.4m,其中O、F、D、E四点在同一条直线上,C、B、F三点在同一条直线上,且OA⊥OE,CF⊥OE,请求出路灯的高度OA.
【答案】路灯的高度OA为4.8m.
【解答】解:∵OA⊥OE,BF⊥OE,
∴BF∥OA,
∴△DFB∽△DOA,△ECF∽△EAO,
∴=,=,
∴,=,
∴OA=OD=4.8(m),
答:路灯的高度OA为4.8m.
45.如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD.
(1)求证:△ABP∽△CDP.
(2)测得AB=2米,BP=3米,PD=12米,求该古城墙的高度CD.
【答案】(1)证明见解析;
(2)古城墙的高度CD为8米.
【解答】(1)证明:∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP,
∵光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,
∴∠APB=∠CPD,
∴△ABP∽△CDP;
(2)解:∵△ABP∽△CDP,
∴,
∴,
∴CD=8,
∴该古城墙的高度CD为8米.
46.某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得FG=6米,CG=20米,请你根据以上数据,计算古塔的高度AB.
【答案】22米.
【解答】解:∵△EDC∽△EBA,△FHG∽△FBA,
∴=,=,
∵DC=HG,
∴=,
∴,
∴CA=40(米),
∵=,
∴,
∴AB=22(米),
答:大雁塔的高度AB为22米.
【考点10 】图形的位似
47.如图,四边形ABCD与四边形EFGH是位似图形,点O是位似中心.若,四边形ABCD的周长是25,则四边形EFGH的周长是( )
A.4B.10C.D.
【答案】B
【解答】解:∵四边形ABCD与四边形EFGH是位似图形,点O是位似中心,
∴=,四边形ABCD与四边形EFGH相似,
∵,
∴=,
∴=,
∴四边形EFGH的周长:四边形ABCD的周长=,
∴四边形EFGH的周长=×25=10.
故选:B.
48.如图,△A′B′C′和△ABC是位似三角形,位似中心为点O,OA'=2AA',则△A′B′C′和△ABC的相似比为( )
A.1:4B.1:3C.4:9D.2:3
【答案】D
【解答】解:∵OA'=2AA',
∴OA:OA'=2:3,
∵△A′B′C和△ABC是位似三角形,
∴AC∥A′C′,
∴△AOC∽△A′OC′,
∴==,
故选:D.
49.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(﹣2,3),先将△ABC绕点(﹣1,0)顺时针旋转90度得到△A1B1C1,再以原点为位似中心作△A1B1C1的位似图形△A2B2C2,若△A1B1C1与△A2B2C2的相似比为1:2,则点A1的对应点A2的坐标是( )
A.(4,2)B.(6,4)
C.(6,4)或(﹣6,﹣4)D.(4,2)或(﹣4,﹣2)
【答案】D
【解答】解:设点P的坐标为(﹣1,0),连接AP、A1P,过点A作AD⊥x轴于D,A1E⊥x轴于E,
由题意得:∠DAP+∠APD=90°,∠EPA1+∠APD=90°,
∴∠DAP=∠EPA1,
在△DAP和△EPA1中,
,
∴△DAP≌△EPA1(AAS),
∴A1E=DP=1,PE=AD=3,
∴点A1的坐标为(2,1),
∵△A1B1C1与△A2B2C2是位似图形,位似比为1:2,
∴点A2的坐标是(4,2)或(﹣4,﹣2),
故选:D.
50.如图,在平面直角坐标系xOy中,△ABC与△ODE是位似图形,各顶点都在格点上,则位似中心的坐标是( )
A.(4,2)B.(5,1 )C.(﹣4,2)D.(0,0)
【答案】A
【解答】解:如图所示:位似中心的坐标是(4,2).
故选:A.
51.在平面直角坐标系中,点A(﹣6,2),B(﹣4,﹣6),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣3,1)B.(﹣2,﹣3)
C.(﹣2,﹣3)或(2,3)D.(﹣3,1)或(3,﹣1)
【答案】D
【解答】解:∵点A(﹣6,2),B(﹣4,﹣6),以原点O为位似中心,相似比为,把△ABO缩小,
∴点A的对应点A′的坐标为(﹣6×)或(﹣6×,2×),
即A'(﹣3,1)或(3,﹣1),
故选:D.
【考点11 】作图-位似
52.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,﹣2).
(1)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O1A1B1,并写出点A1的坐标;
(2)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1,并写出点A的对应点A2的坐标;
【答案】(1)画图见解析,A1(0,2)
(2)画图见解析,A2(4,2)
【解答】解:(1)如图所示△O1A1B1即为所求,A1(0,2);
(2)如图所示,△OA2B2即为所求,A2(4,2)
53.如图,请画出△ABC的一个位似图形△A1B1C1,使△ABC与△A1B1C1以O为位似中心,且相似比为2:1.
【答案】见解析.
【解答】解:如图所示,△A1B1C1,△A'B'C'即为所求(作出一个即可).
54.图①、图②、图③都是6×6的网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.点A,B,C均在格点上.在图①、图②、图③给定的网格中,仅用无刻度的直尺,按下列要求完成作图,并保留作图痕迹.
(1)在图①中,以点C为位似中心,将△ABC放大到原来的2倍;
(2)在图②中,在线段BC上作点D,使得CD=3BD;
(3)在图③中,作△BEF∽△BAC,且相似比为3:4.
【答案】(1)见解答.
(2)见解答.
(3)见解答.
【解答】解:(1)如图①,△A'B'C即为所求.
(2)如图②,取格点M,N,使,连接MN交BC于点D,
可知△BDM∽△CDN,
∴,
∴CD=3BD,
则点D即为所求.
(3)∵△BEF∽△BAC,且相似比为3:4,
∴,
如图③,△BEF即为所求.
专题04 一次函数(考点清单) -八年级上学期数学期末考点大串讲(北师大版): 这是一份专题04 一次函数(考点清单) -八年级上学期数学期末考点大串讲(北师大版),文件包含专题04一次函数考点清单原卷版docx、专题04一次函数考点清单解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
专题08 圆(考点清单,12个考点)-九年级上学期数学期末考点大串讲(北师大版): 这是一份专题08 圆(考点清单,12个考点)-九年级上学期数学期末考点大串讲(北师大版),文件包含专题08圆考点清单12个考点原卷版docx、专题08圆考点清单12个考点解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
专题05 反比例函数(考点清单,7个考点)-九年级上学期数学期末考点大串讲(北师大版): 这是一份专题05 反比例函数(考点清单,7个考点)-九年级上学期数学期末考点大串讲(北师大版),文件包含专题05反比例函数考点清单7个考点原卷版docx、专题05反比例函数考点清单7个考点解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。












