数学九年级上册4.3 相似三角形多媒体教学课件ppt

这是一份数学九年级上册4.3 相似三角形多媒体教学课件ppt，共29页。PPT课件主要包含了知识点，相似比等内容，欢迎下载使用。

1．理解并掌握相似三角形周长之比等于相似比和面积之比等于相似比的平方的性质.2．能运用相似三角形的有关性质解决简单问题.
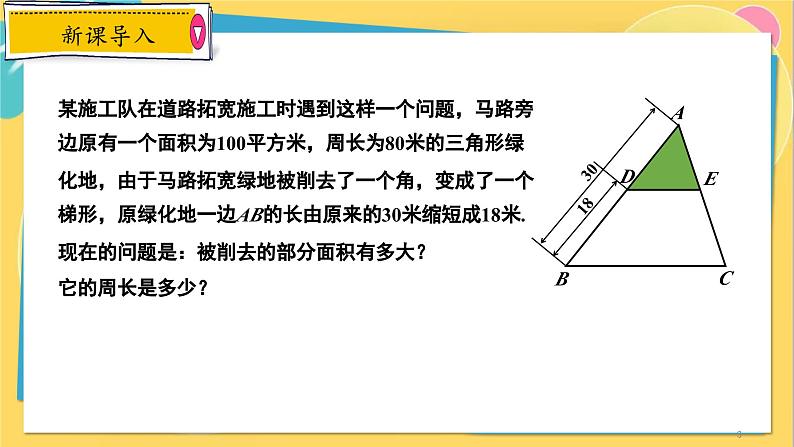
某施工队在道路拓宽施工时遇到这样一个问题，马路旁边原有一个面积为100平方米，周长为80米的三角形绿化地，由于马路拓宽绿地被削去了一个角，变成了一个梯形，原绿化地一边AB的长由原来的30米缩短成18米. 现在的问题是：被削去的部分面积有多大？它的周长是多少？
相似三角形的周长比和面积比
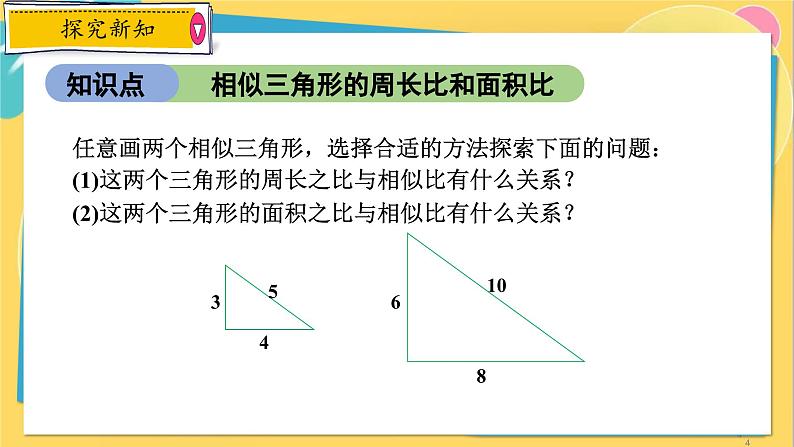
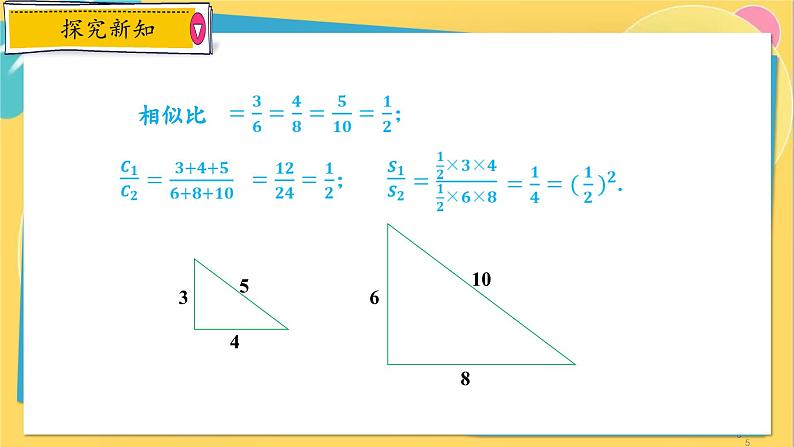
任意画两个相似三角形，选择合适的方法探索下面的问题：(1)这两个三角形的周长之比与相似比有什么关系？(2)这两个三角形的面积之比与相似比有什么关系？
已知:△ABC∽△A´B´C´，相似比为k.
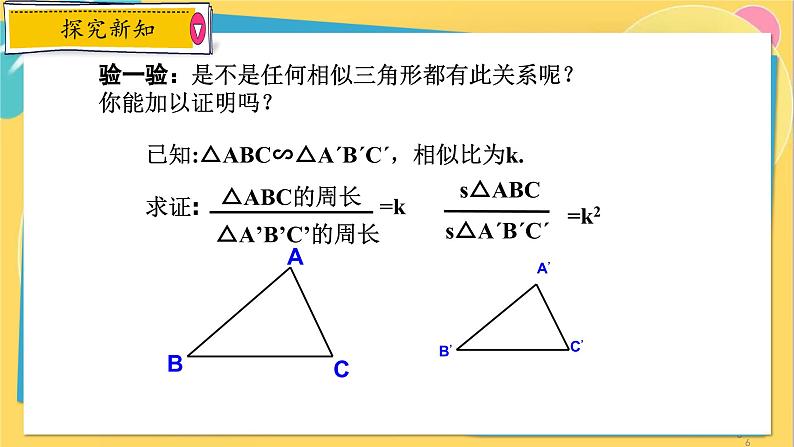
验一验：是不是任何相似三角形都有此关系呢？你能加以证明吗？
如图，分别作△ABC，△A′B′C′的BC， B′C′边上的高线AD，A′D′.∵△ABC∽△A′B′C′，∴∠B=∠B′（相似三角形的对应角相等）.∵AD，A′D′分别是BC， B′C′边上的高线，∴∠ADB=∠A′D′B′=90°，
如图，D，E分别是AC，AB上的点，∠ADE=∠B，AG⊥BC于点G，AF⊥DE于点F. 若AD=3，AB=5，求：(2)△ADE与△ABC的周长之比.(3)△ADE与△ABC的面积之比.
解： △ADE与△ABC的周长之比是3:5（相似三角形的周长之比等于相似比）.
△ADE与△ABC的面积之比是9:25（相似三角形的面积之比等于相似比的平方）.
相似三角形的周长之比等于相似比；相似三角形的面积之比等于相似比的平方.
相似三角形的周长和面积有以下性质：
两个相似三角形的对应高之比等于相似比。
类似地，相似三角形对应中线的比与对应角平分线的比也等于相似比。
如图是某市部分街道图，比例尺为1:100 000. 请估计三条道路围成的三角形地块ABC的实际周长和面积.
如图，△ABC∽△A′B′C′，BC=6，B′C′=4，AD⊥BC于点 D，AD=4，求△A′B′C′的面积.
【分析】利用相似三角形的面积的比等于相似比的平方求解.
如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E. 若要使△ADE与四边形DBCE的面积相等，则AD与AB的比应取多少？
将上面生活中的问题转化为数学问题是：如图，已知DE∥BC，AB＝30 m，BD＝18 m，△ABC的周长为80 m，求△ADE的面积和周长分别是多少？解：∵DE∥BC，∴∠ADE＝∠B，∠AED＝∠C，∴△ADE∽△ABC，∴ ,∴ ，∴ =32 m.∴ △ADE的周长为32m.
将上面生活中的问题转化为数学问题是：如图，已知DE∥BC，AB＝30 m，BD＝18 m，△ABC的周长为80 m，求△ADE的面积和周长分别是多少？
∴ △ADE的面积为16 m2.
【2023·重庆】若两个相似三角形周长的比为1：4，则这两个三角形对应边的比是(　　)A．1∶2 B．1∶4 C．1∶8 D．1∶16
【2024·金华期末】两个相似三角形的最短边分别是5 cm和3 cm，它们的周长之差为12 cm，则小三角形的周长为(　　)A．14 cm B．16 cm C．18 cm D．30 cm
【2023·宁波一模】如图，在△ABC中，DE∥BC，DB＝2AD，△ADE的面积为1，则△ABC的面积为(　　)A．4B．6C．8D．9