

2023-2024学年山东省济南市育英教育集团七年级(下)期中数学试卷(含解析)
展开1.计算(ab)2的结果是( )
A. a2bB. ab2C. 2abD. a2b2
2.华为麒麟990芯片采用了最新的0.000000007米的工艺制程,数0.000000007用科学记数法表示为( )
A. 7×10−9B. 7×10−8C. 0.7×10−9D. 0.7×10−8
3.在△ABC中,∠A:∠B:∠C=3:4:7,则△ABC的形状是( )
A. 锐角三角形B. 钝角三角形C. 直角三角形D. 无法确定
4.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据如下:下列说法错误的是( )
A. 在这个变化中,自变量是温度,因变量是声速
B. 温度越低,声速越慢
C. 在一定范围内,当温度每升高10°C,声速增加6m/s
D. 当空气温度为20°C时,声音5s可以传播1700m
5.一个不等边三角形的两边长分别为6和10,且第三边长为偶数,符合条件的三角形有( )
A. 2个B. 3个C. 4个D. 5个
6.已知:如图,甲、乙两个工程队合作修一条长为3000米的公路,假设甲、乙两个工程队的工作效率是一定的.甲队单独做了20天后,乙队加入合作完成剩下的全部工程.完成的工程量y(米)与工程时间x(天)的关系如图所示.下列结论中错误的是( )
A. 完成该工程一共用了30天
B. 乙工程队在该工程中一共工作了10天
C. 甲工程队每天修路50米
D. 乙工程队每天修路200米
7.如图,点A、B、C、D在同一直线上,AE//DF,AB=CD,添加以下条件不能判定△AEC≌△DFB的是( )
A. AE=DF
B. ∠E=∠F
C. EC=BF
D. EC//BF
8.如图,∠AOB与∠EO′F,分别以O,O′为圆心,以同样长为半径画弧,分别交OA,OB于点A′,B′,交O′E,O′F于点E′,F′.以B′为圆心,以E′F′长为半径画弧,交弧A′B′于点H.下列结论不正确的是( )
A. ∠AOB=2∠EO′FB. ∠AOB>∠EO′F
C. ∠HOB=∠EO′FD. ∠AOH=∠AOB−∠EO′F
9.现有一块如图所示的四边形草地ABCD,经测量,∠B=∠C,AB=10m,BC=8m,CD=12m,点E是AB边的中点.小狗汪汪从点B出发以2m/s的速度沿BC向点C跑,同时小狗妞妞从点C出发沿CD向点D跑,若能够在某一时刻使△BEP与△CPQ全等,则妞妞的运动速度为( )
A. 32m/s
B. 52m/s
C. 2m/s或32m/s
D. 2m/s或52m/s
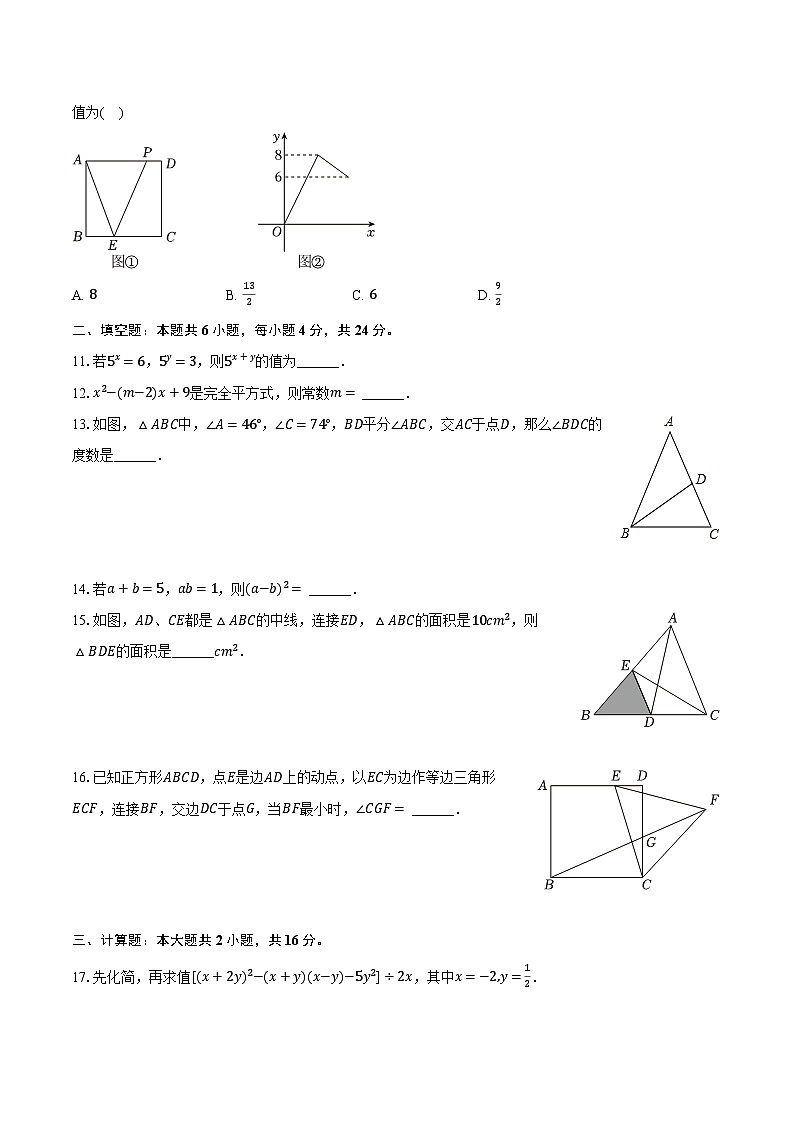
10.如图①,在正方形ABCD的边BC上有一点E,连接AE.点P从正方形的顶点A出发,沿A→D→C以1cm/s的速度匀速运动到点C.图②是点P运动时,△APE的面积y(cm2)随时间x(s)变化的函数图象.当x=7时,y的值为( )
A. 8B. 132C. 6D. 92
二、填空题:本题共6小题,每小题4分,共24分。
11.若5x=6,5y=3,则5x+y的值为______.
12.x2−(m−2)x+9是完全平方式,则常数m= ______.
13.如图,△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是______.
14.若a+b=5,ab=1,则(a−b)2= ______.
15.如图,AD、CE都是△ABC的中线,连接ED,△ABC的面积是10cm2,则△BDE的面积是______cm2.
16.已知正方形ABCD,点E是边AD上的动点,以EC为边作等边三角形ECF,连接BF,交边DC于点G,当BF最小时,∠CGF= ______.
三、计算题:本大题共2小题,共16分。
17.先化简,再求值[(x+2y)2−(x+y)(x−y)−5y2]÷2x,其中x=−2,y=12.
18.如图,在△ABC中,AB=AC,点D在BC边上,点E在AC边上,连结AD,DE.已知∠1=∠2,AD=DE.
(1)求证:△ABD≌△DCE.
(2)若BD=2,CD=5,求AE的长.
四、解答题:本题共8小题,共70分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
解答下列各题:
(1)计算:(−3)3−|−14|+(13)−3+(π−3)0;
(2)(2a2b)3⋅(−7ab2)÷14a4b3.
20.(本小题8分)
如图,在△ABC中,AD为边BC上的高,点E为边BC上的一点,连接AE.
(1)当AE为边BC上的中线时,若AD=6,△ABC的面积为24,求CE的长;
(2)当AE为∠BAC的平分线时,若∠C=66°,∠DAE=15°,求∠B度数.
21.(本小题8分)
画图题:
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.
(2)判断EF、GH的位置关系是______.
(3)连接AC和BC,则三角形ABC的面积是______.
22.(本小题8分)
某剧院的观众席的座位为扇形,且按下列方式设置:
(1)按照上表所示的规律,当排数为6时,此时座位数为______.
(2)写出座位数y与排数x之间的关系式:______.
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
23.(本小题8分)
为了体验大学校园文化,小锋利用周末骑电动车从家出发去西安交通大学,当他骑了一段路时,想起要帮在该校读书的姐姐买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往西安交通大学,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小锋家距离西安交通大学______米,他在新华书店停留了______分钟;
(2)本次去西安交通大学的途中,小锋一共行驶了______米;
(3)小峰在前12分骑车的平均速度是多少?买到书后,小锋从新华书店到西安交通大学骑车的平均速度是多少?
24.(本小题8分)
为了解学生对所学知识的应用能力,某校老师在七年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离,甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可.
乙:如图2,先确定直线AB,过点B作直线BE,在直线BE上找可以直接到达点A的一点D,连接DA,作∠ADB=∠BDC,交直线AB于点C,最后测量BC的长即可.
(1)甲、乙两同学的方案哪个可行?并说明理由.
(2)请将不可行的方案稍加修改使之可行,你的修改是:______ ,请说明理由.
25.(本小题10分)
在数学课本第12章《整式乘除》里学习了两数和的平方公式,还记得它是如何被发现的吗?
如图1的面积,把图1看作一个大正方形,它的面积是(a+b)2,如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2,由此得到:(a+b)2=a2+2ab+b2.
类比探究一:
(1)如图2,正方形ABCD是由四个边长分别是a,b的长方形和中间一个小正方形组成的,用不同的法对图2的面积进行计算,你发现的等式是______(用a,b表示);
类比探究二:
(2)如图3,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,对图3的面积进行计算,你发现的式子是______
(用a,b,c表示,结果化为最简);
应用探索结果解决问题:
(3)如图3,正方形ABCD的边长是c,它由四个直角边长分别是a,b的角三角形和中间一个小正方形组成的,当c=5,a−b=1时,求a+b的值.
(4)如图4,将四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH.若该图形的周长为80,OA=12.则该图形的面积为______.
26.(本小题12分)
【基础巩固】(1)如图1,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:△AEC≌△ADB;
【尝试应用】(2)如图2,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,B、D、E三点在一条直线上,AC与BE交于点F,若点F为AC中点,
①求∠BEC的大小;
②CE=2,求△ACE的面积;
【拓展提高】(3)如图3,△ABC与△ADE中,AB=AC,DA=DE,∠BAC=∠ADE=90°,BE与CA交于点F,DC=DF,CD⊥DF,△BCF的面积为18,求AF的长.
答案和解析
1.【答案】D
【解析】解:(ab)2=a2b2.
故选:D.
利用积的乘方的法则:先把积中的每一个乘数分别乘方,再把所得的幂相乘,从而可求解.
本题主要考查积的乘方,解答的关键是对积的乘方的法则的掌握与运用.
2.【答案】A
【解析】解:数0.00 0000007用科学记数法表示为7×10−9.
故选:A.
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10−n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为a×10−n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
3.【答案】C
【解析】解:设∠A、∠B、∠C分别为3k、4k、7k,
∵3k+4k=7k,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形.
故选:C.
根据比例设∠A、∠B、∠C分别为3k、4k、7k,然后利用三角形的内角和定理求出∠C的度数,即可判断三角形的形状.
本题考查了三角形内角和定理,熟知三角形内的角和是180°是本题的关键.
4.【答案】D
【解析】解:A.∵在这个变化中,自变量是温度,因变量是声速,
∴选项A说法正确;
B.∵根据数据表,可得温度越低,声速越慢,
∴选项B说法正确;
C.∵324−318=6(m/s),330−324=6(m/s),336−330=6(m/s),342−336=6(m/s),348−342=6(m/s),
∴当温度每升高10°C,声速增加6m/s,
∴选项C说法正确;
D.∵342×5=1710(m),
∴当空气温度为20°C时,声音5s可以传播1710m,
∴选项D说法错误.
故选:D.
根据自变量、因变量的含义,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
此题考查了自变量、因变量的含义,以及用表格表示变量之间的关系,列表法能具体地反映自变量与函数的数值对应关系,在实际生活中应用非常广泛;解析式法准确地反映了函数与自变量之间的对应规律,根据它可以由自变量的取值求出相应的函数值,反之亦然;图象法直观地反映函数值随自变量的变化而变化的规律.
5.【答案】B
【解析】解:设第三边长为x,
根据题意得10−6
∴x为8、12、14,符合条件的三角形有3个,
故选:B.
设第三边长为x,根据三角形三边的关系得4
6.【答案】D
【解析】解:从图象可知,工程时间x=30,所对应的是y=3000,
∴完成该工程一共用了30天,故A是正确的;
∵30−20=10(天),
∴乙工程队在该工程中一共工作了10天,故B是正确的;
∵甲队单独做了20天,完成1000米,
∴1000÷20=50,
即甲工程队每天修路50米;故C是正确的;
设乙工程队每天修路x米,
则3000−1000=10×(x+50),
解得x=150,
∴乙工程队每天修路150米,故D是错误的,
故选:D.
根据甲队单独做了20天,完成1000米,得出甲工程队每天修路50米,因为甲、乙两个工程队的工作效率是一定的,则列式3000−1000=10×(x+50),得出乙工程队每天修路150米,结合图象性质,即可作答.
本题考查了函数图象获取信息以及一元一次方程的工程问题,正确掌握相关性质内容是解题的关键.
7.【答案】C
【解析】解:∵AE//DF,
∴∠A=∠D,
∵AB=CD,
∴AC=DB,
∴A、添加条件AE=DF,可以利用SAS定理证明△AEC≌△DFB,故此选项不合题意;
B、添加条件∠E=∠F,利用AAS能证明△AEC≌△DFB,故此选项不合题意;
C、添加条件EC=BF,不能证明△AEC≌△DFB,故此选项符合题意;
D、添加条件EC//BF,可得∠ACE=∠DBF,可以利用ASA定理证明△AEC≌△DFB,故此选项不合题意;
故选:C.
根据题目条件可得AC=DB,∠A=∠D,再根据四个选项结合全等三角形的判定定理可得答案.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
8.【答案】A
【解析】解:根据作图可知∠EO′F=∠HOB,
A.不能判断∠AOB=2ㄥEOF,故该选项不正确,符合题意;
B.由于∠AOB>∠HOB,即∠AOB>∠EO′F,故该选项正确,不符合题意;
C.∠HOB=∠EO′F,故该选项正确,不符合题意;
D.∠AOH=∠AOB−∠HOB=∠AOB−∠EOF,故该选项正确,不符合题意.
故选:A.
根据作图可知∠EO′F=∠HOB,结合图形,根据角度的和差关系逐项分析判断即可求解.
本题考查了,角度的计算及作图,掌握基本作图是解题的关键.
9.【答案】D
【解析】解:∵AB=10m,E是AB边的中点,
∴BE=5m,
∵∠B=∠C,且△BEP与△CPQ全等,
∴BP=CQ,BE=CP或CP=BP,BE=CQ,
当BP=CQ,BE=CP时,
∵BE=5m,BC=8m,
设运动时间为t,8−2t=5,解得t=32,
∴CQ=BP=2×32=3,
此时妞妞的运动速度为:3÷32=2m/s,
当CP=BP,BE=CQ时,2t=82,t=2,
此时CQ=5,妞妞的运动速度为:5÷2=52m/s,
故选:D.
根据三角形全等性质分BP=CQ,BE=CP或CP=BP,BE=CQ两类讨论求解即可得到答案.
本题考查三角形全等动点问题,解题的关键是掌握全等三角形的性质,进行分类讨论.
10.【答案】B
【解析】解:设正方形的边长为a,
①当点P在点D时,y=12AB×AD=12×a×a=8,解得:a=4,
②当点P在点C时,y=12EP×AB=12×EP×4=6,解得:EP=3,即EC=3,BE=1,
③当x=7时,如图所示:
此时,PC=1,PD=7−4=3,
当x=7时,y=S正方形ABCD−(S△ABE+S△ECP+S△APD)=4×4−12(4×1+1×3+4×3)=132.
故选:B.
①当点P在点D时,y=12AB×AD=12×a×a=8,解得:a=4,②当点P在点C时,y=12EP×AB=12×EP×4=6,解得:EP=3,即EC=3,BE=1,③当x=7时,y=S正方形ABCD−(S△ABE+S△ECP+S△APD,即可求解.
本题考查的是动点图象问题,此类问题关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.
11.【答案】18
【解析】解:∵5x=6,5y=3,
∴5x+y
=5x⋅5y
=6×3
=18,
故答案为:18.
根据已知条件,逆用同底数幂的乘法法则把所求代数式写成含有5x,5y的形式,再整体代入计算即可.
本题主要考查了同底数幂的乘法运算,解题关键是熟练掌握同底数幂相乘法则.
12.【答案】8或−4
【解析】解:∵x2−(m−2)x+9是完全平方式,
∴−(m−2)x=±2⋅x⋅3,
解得:m=8或−4.
故答案为:8或−4.
根据完全平方式得出−(m−2)x=±2⋅x⋅3,再求出m即可.
本题考查了完全平方式,能熟记完全平方式(完全平方式有a2+2ab+b2和a2−2ab+b2两个)是解此题的关键.
13.【答案】76°
【解析】解:∵∠A=46°,∠C=74°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠DBC=30°,
∴△BCD中,∠BDC=180°−∠C−∠DBC=76°,
故答案为:76°
先根据三角形内角和,得到∠ABC的度数,再根据角平分线的定义,得出∠DBC,进而根据三角形内角和,即可得到∠BDC的度数.
本题主要考查了三角形内角和定理的运用,解题时注意:三角形内角和等于180°.
14.【答案】21
【解析】解:∵a+b=5,
∴(a+b)2=25,
∴a2+2ab+b2=25,
∵ab=1,
∴a2+b2=23,
∴(a−b)2=a2−2ab+b2=23−2×1=21,
故答案为:21.
先根据完全平方公式求出a2+b2=23,再根据完全平方公式将要求的式子展开计算即可.
本题考查了完全平方公式,熟记这个公式是解题的关键.
15.【答案】2.5
【解析】解:∵AD是△ABC的中线,△ABC的面积是10cm2,
∴△ABD的面积=△ABC的面积×12=5(cm2),
∵E是AB的中点,
∴△BDE的面积=△ABD的面积×12=2.5(cm2),
故答案为:2.5.
根据三角形的中线把三角形分为面积相等的两部分计算即可.
本题考查的是三角形的中线,熟记三角形的中线把三角形分为面积相等的两部分是解题的关键.
16.【答案】120°
【解析】解:作等边三角形CDH,连接FH,
由正方形ABCD,等边三角形ECF,
得△ECD≌△FCH(SAS),
得∠CHF=∠CDE=90°,
故当BF⊥HF时BF最小,此时BF//CH,
得∠CGF=180°−∠DCH=120°.
故答案为:120°.
作等边三角形CDH,连接FH,由正方形ABCD,等边三角形ECF,得△ECD≌△FCH(SAS),得∠CHF=∠CDE=90°,故当BF⊥HF时BF最小,此时BF//CH,即可得∠CGF=180°−∠DCH=120°.
本题主要考查了正方形中的计算,解题关键是构造全等三角形.
17.【答案】解:原式=[x2+4xy+4y2−x2+y2−5y2]÷2x,
=4xy÷2x,
=2y,
当x=−2、y=12时,原式=2y=1.
【解析】根据完全平方公式、平方差公式及整式的混合运算,将原式化简为2y,代入y值即可求出结论.
本题考查了整式的化简求值,将原式化简为2y是解题的关键.
18.【答案】(1)证明:∵AB=AC,
∴∠B=∠C,
在△ABD与△DCE中,
∠B=∠C∠1=∠2AD=DE
∴△ABD≌△DCE(AAS);
(2)解:∵△ABD≌△DCE,
∴AB=DC=5,CE=BD=2,
∵AC=AB,
∴AC=5,
∴AE=AC−EC=AB−EC=5−2=3.
【解析】(1)根据AAS可证明△ABD≌△DCE;
(2)得出AB=DC=5,CE=BD=2,求出AC=5,则AE可求出.
本题考查了全等三角形的判定与性质,等腰三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.
19.【答案】解:(1)原式=−27−14+27+1
=34;
(2)原式=8a6b3⋅(−7ab2)÷14a4b3
=−56a7b5÷14a4b3
=−4a3b2.
【解析】(1)先算乘方,再算加减;
(2)先算乘方,再从左到右依次计算.
本题考查实数运算和整式混合运算,解题的关键是掌握实数相关运算法则和整式相关的运算法则.
20.【答案】解:(1)∵AD为边BC上的高,AD=6,△ABC的面积为24,
∴12BC×6=24,
∴BC=8,
∵AE为边BC上的中线,
∴CE=12BC=12×8=4;
(2)∵AD为边BC上的高,
∴∠ADC=90°,
∵∠C=66°,
∴∠CAD=90°−∠C=90°−66°=24°,
∵∠DAE=15°,
∴∠CAE=∠DAE+∠CAD=15°+24°=39°,
∵AE为∠BAC的平分线,
∴∠BAC=2∠CAE=2×39°=78°,
∴∠B=180°−∠BAC−∠C=180°−78°−66°=36°.
【解析】(1)根据三角形的面积公式求出BC的长,再根据三角形的中线的定义即可求出CE的长;
(2)先求出∠CAD的度数,即可求出∠CAE的度数,再根据角平分线的定义即可求出∠BAC的度数,最后根据三角形内角和定理即可求出∠B的度数.
本题考查了三角形的面积,三角形的中线、角平分线、高,三角形内角和定理,熟练掌握这些知识点是解题的关键.
21.【答案】EF⊥GH;10
【解析】解:(1)如图,
(2)EF、GH的位置关系是EF⊥GH,
故答案为:EF⊥GH.
(3)如图,连接AC和BC,
设小方格的边长为1,则三角形ABC的面积是12×4×5=10.
故答案为:10.
(1)过点C作5×1的矩形的对角线所在的直线,可得AB的垂线和平行线;
(2)易得EF与GH的位置关系是:垂直;
(3)设小方格的边长为1,利用三角形的面积求解即可.
本题主要考查了基本作图,解题的关键是利用方格正确的作出图形.
22.【答案】解:(1)65;
(2)y=3x+47;
(3)把y=90代入得,90=3x+47,
解得x=433,不符合题意,
所以不可能某一排90个座位.
【解析】【分析】
本题考查函数关系式,理解题目中的数量关系是正确解答的前提.
(1)根据座位数与排数变化规律得出答案;
(2)根据变化规律得出一般性的函数关系式;
(3)代入计算即可.
【解答】
解:(1)由表格中座位数与排数的变化规律可知,排数每增加1排,座位数就增加3个,
所以第6排的座位数为:50+3×(6−1)=65(个),
故答案为:65;
(2)由座位数随着排数增加的变化规律可得,
y=50+3(x−1)=3x+47,
故答案为:y=3x+47;
(3)见答案.
23.【答案】4500 8 5500
【解析】解:(1)根据图象可知,小锋家距离西安交通大学4500米;
∵16~24分钟的路程没变,
∴24−16=8(分钟),
∴小锋在新华书店停留了8分钟.
(2)由图象可知:本次去西安交通大学的途中,小锋一共行驶的路程为:3500+500+1500=5500(米).
(3)由图象可知,小峰在前12分行驶的路程为3500米,
∴小峰在前12分骑车的平均速度为:350012=8753(米/分);
买到书后,小锋从新华书店到西安交通大学行驶的路程为:(4500−3000)米,所用的时间为:(28−24)分钟,
∴从新华书店到西安交通大学的平均速度为:(4500−3000)÷(28−24)=375(米/分),
∴小锋从新华书店到西安交通大学骑车的平均速度是375米/分.
(1)根据函数图象中纵轴可得到小锋家到西安交通大学的距离,16~24分钟的路程没变,可得到他在新华书店停留的时间;
(2)根据函数图象可知,本次去西安交通大学的途中小锋一共行驶的路程和;
(3)根据小峰在前12分的距离与所用的时间可求出小峰在前12分的平均速度,再根据买到书后,小锋从新华书店到西安交通大学的距离与所用的时间可求出小峰骑车的平均速度.
本题考查函数图象,能熟练的从函数图象中获得信息是解题的关键.
24.【答案】DB⊥AC
【解析】解:(1)甲同学的方案可行.
理由:由题意得,
在△ABO与△CDO中,
OA=OC∠AOB=∠CODOB=OD,
∴△ABO≌△CDO(SAS),
∴AB=CD,
故甲同学的方案可行.
(2)DB⊥AC;
理由:在△DBA与△DBC中,
∠ADB=∠CDBDB=DB∠DBA=∠DBC,
∴△DBA≌△DBC(ASA),
∴AB=CB.
故答案为:DB⊥AC.
(1)甲同学作出的是全等三角形,然后根据全等三角形对应边相等测量的,所以是可行的;
(2)甲根据全等三角形的判定和性质定理即可得到结论.
本题主要考查了全等三角形的应用,熟练掌握全等三角形的判定定理是解决问题的关键.
25.【答案】(a+b)2−4ab=(a−b)2 c2=a2+b2 120
【解析】解:(1)如图2,∵正方形ABCD是由四个边长分别是a,b的长方形和中间一个小正方形组成,
∴(a+b)2=4ab+(a−b)2,
∴(a+b)2−4ab=(a−b)2.
故答案为:(a+b)2−4ab=(a−b)2;
(2)∵正方形ABCD的边长是c,
∴正方形ABCD的面积为c2.
∵正方形ABCD由四个直角边长分别是a,b的角三角形和中间一个小正方形组成,
∴c2=4×12ab+(a−b)2,
∴c2=2ab+a2−2ab+b2,
∴c2=a2+b2.
故答案为:c2=a2+b2;
(3)∵正方形ABCD的边长是c,c=5,
∴正方形ABCD的面积为25.
∵正方形ABCD由四个直角边长分别是a,b的角三角形和中间一个小正方形组成,
∴c2=4×12ab+(a−b)2,
∵a−b=1,
∴25=2ab+1,
∴ab=12.
∴(a+b)2=(a−b)2+4ab=1+48=49,
∵a+b>0,
∴a+b=7;
(4)设OB=x,则AH=DE=BC=BF=12−x,
有勾股定理得:AB=BH=FE=CD= 122+x2,
∵图形ABCDEFGH的周长为80,
∴4 144+x2+4(12−x)=80,
解得:x=5,
∴OB=5,
∴S△OAB=12×OB⋅OA=30,
∴该图形的面积为4×S△OAB=120.
故答案为:120.
(1)利用大正方形的面积减去4个小长方形的面积等于中间小正方形的面积即可得出结论;
(2)利用大正方形的面积等于小正方形的面积与4个全等直角三角形的面积和表示,化简整理即可得出结论;
(3)利用大正方形的面积等于小正方形的面积与4个全等直角三角形的面积和表示,再利用整体代入的方法和算术平方根的意义解答即可;
(4)设OB=x,利用已知条件和勾股定理列出方程,解方程求得x值,再利用图形的面积为4个直角三角形的面积之和解答即可.
本题主要考查了完全平方式,正方形,矩形的面积,直角三角形的面积,完全平方公式的几何背景,勾股定理的几何背景,熟练掌握完全平方式是解题的关键.
26.【答案】(1)证明:∵∠BAC=∠DAE,
∴∠BAC−∠BAE=∠DAE−∠BAE,
即∠CAE=∠BAD,
在△AEC和△ADB中,
AC=AB∠CAE=∠BADAE=AD,
∴△AEC≌△ADB(SAS);
(2)解:①∵AD=AE,∠DAE=90°,
∴∠ADE=∠AED=45°,
∴∠ADB=180°−∠ADE=180°−45°=135°,
同(1)得:△AEC≌△ADB(SAS),
∴∠AEC=∠ADB=135°,
∴∠BEC=∠AEC−∠AED=135°−45°=90°;
②如图2,过点A作AG⊥DE于点G,
则∠FGA=90°,
由①可知,∠FEC=90°,
∴∠FGA=∠FEC,
∵点F为AC中点,
∴AF=CF,
又∵∠AFG=∠CFE,
∴△AGF≌△CEF(ASA),
∴AG=CE=2,GF=EF,
∵AD=AE,∠DAE=90°,
∴DG=EG=AG=2,
∴GF=EF=12EG=1,
∴S△ACE=2S△CEF=2×12CE⋅EF=2×1=2;
(3)解:如图3,连接CE,
同(2)得:△CDE≌△FDA(SAS),
∴CE=AF,∠DCE=∠DFA=135°,
∴∠ACE=∠DCE−∠ACB=135°−45°=90°,
在△ACE和△BAF中,
AC=AB∠ACE=∠BAF=90°CE=AF,
∴△ACE≌△BAF(SAS),
∴CE=AF,S△ACE=S△BAF,
∵∠ACE=∠BAC,
∴CE//AB,
∴S△ABE=S△ABC=12AC⋅AB=12AC2,
∵S△ABC+S△ACE−S△ABE−S△CEF=S△BCF,
∴12AC2+12AC⋅CE−12AC2−12CE⋅CF=18,
∴AC⋅AF−AF⋅CF=36,
∴AF(AC−CF)=36,
∴AF2=36,
∴AF= 36=6,
即AF的长为6.
【解析】(1)由SAS证△AEC≌△ADB即可;
(2)①同(1)得△AEC≌△ADB(SAS),得∠AEC=∠ADB=135°,即可得出结论;
②过点A作AG⊥DE于点G,证△AGF≌△CEF(ASA),得AG=CE=2,GF=EF,再由等腰直角三角形的性质得DG=EG=AG=2,则GF=EF=1,然后由三角形面积关系即可得出结论;
(3)连接CE,同(2)得△CDE≌△FDA(SAS),则CE=AF,∠DCE=∠DFA=135°,得∠ACE=90°,再证△ACE≌△BAF(SAS),得CE=AF,S△ACE=S△BAF,然后证CE//AB,得S△ABE=S△ABC=12AC2,进而由S△ABC+S△ACE−S△ABE−S△CEF=S△BCF,得AC⋅AF−AF⋅CF=36,则AF2=36,即可得出结论.
本题是三角形综合题目,考查了等腰直角三角形的性质、全等三角形的判定与性质、平行线的判定与性质以及三角形面积等知识,本题综合性强,熟练掌握等腰直角三角形的性质,证明三角形全等是解题的关键,属于中考常考题型.温度/℃
−20
−10
0
10
20
30
声速/m/s
318
324
330
336
342
348
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
2023-2024学年山东省济南市育英教育集团八年级(下)期中数学试卷: 这是一份2023-2024学年山东省济南市育英教育集团八年级(下)期中数学试卷,共21页。试卷主要包含了已知两个分式等内容,欢迎下载使用。
2023-2024学年宁夏银川九中教育集团七年级(下)期中数学试卷(含解析): 这是一份2023-2024学年宁夏银川九中教育集团七年级(下)期中数学试卷(含解析),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省济南市市中区育英中学七年级(下)期中数学试卷(含解析): 这是一份2022-2023学年山东省济南市市中区育英中学七年级(下)期中数学试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












