2023-2024学年北京市朝阳区陈经纶中学高一（下）期中数学试卷（含解析）

这是一份2023-2024学年北京市朝阳区陈经纶中学高一（下）期中数学试卷（含解析），共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1.在复平面内，复数z对应的点在第三象限，则复数z⋅(1+i)2024对应的点在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
2.已知正四棱锥的底面边长为2，高为3，则它的体积为( )
A. 2B. 4C. 6D. 12
3.已知非零向量OA，OB不共线，且BM=13BA，则向量OM=( )
A. 13OA+23OBB. 23OA+13OBC. 13OA−23OBD. 13OA−43OB
4.如图，飞机飞行的航线AB和地面目标C在同一铅直平面内，在A处测得目标C的俯角为30°，飞行10千米到达B处，测得目标C的俯角为75°，这时B处与地面目标C的距离为( )
A. 5千米B. 5 2千米C. 4千米D. 4 2千米
5.设a，b是非零向量，则“存在实数λ，使得a=λb”是“|a+b|=|a|+|b|”的( )
A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
6.如图，四棱锥P−ABCD的底面ABCD是梯形，AB/​/CD，若平面PAD∩平面PBC=l，则( )
A. l/​/CDB. l/​/BCC. l与直线AB相交D. l与直线DA相交
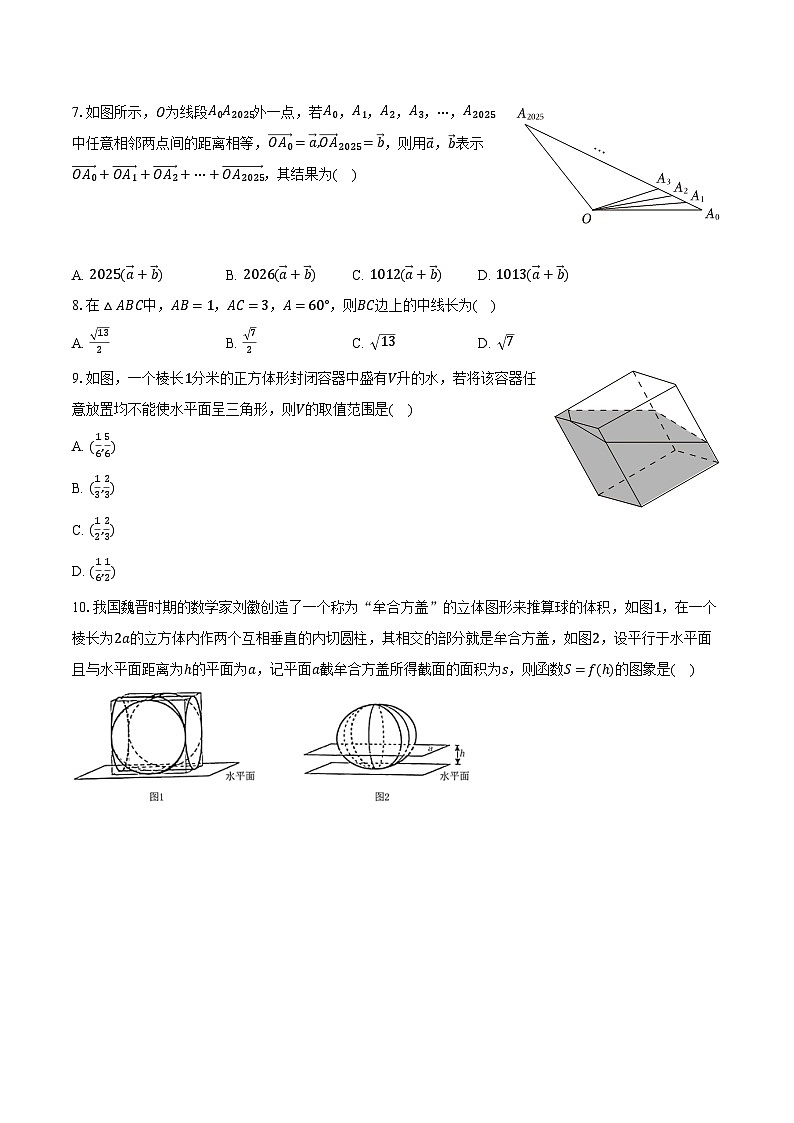
7.如图所示，O为线段A0A2025外一点，若A0，A1，A2，A3，⋯，A2025中任意相邻两点间的距离相等，OA0=a,OA2025=b，则用a，b表示OA0+OA1+OA2+⋯+OA2025，其结果为( )
A. 2025(a+b)B. 2026(a+b)C. 1012(a+b)D. 1013(a+b)
8.在△ABC中，AB=1，AC=3，A=60°，则BC边上的中线长为( )
A. 132B. 72C. 13D. 7
9.如图，一个棱长1分米的正方体形封闭容器中盛有V升的水，若将该容器任意放置均不能使水平面呈三角形，则V的取值范围是( )
A. (16,56)
B. (13,23)
C. (12,23)
D. (16,12)
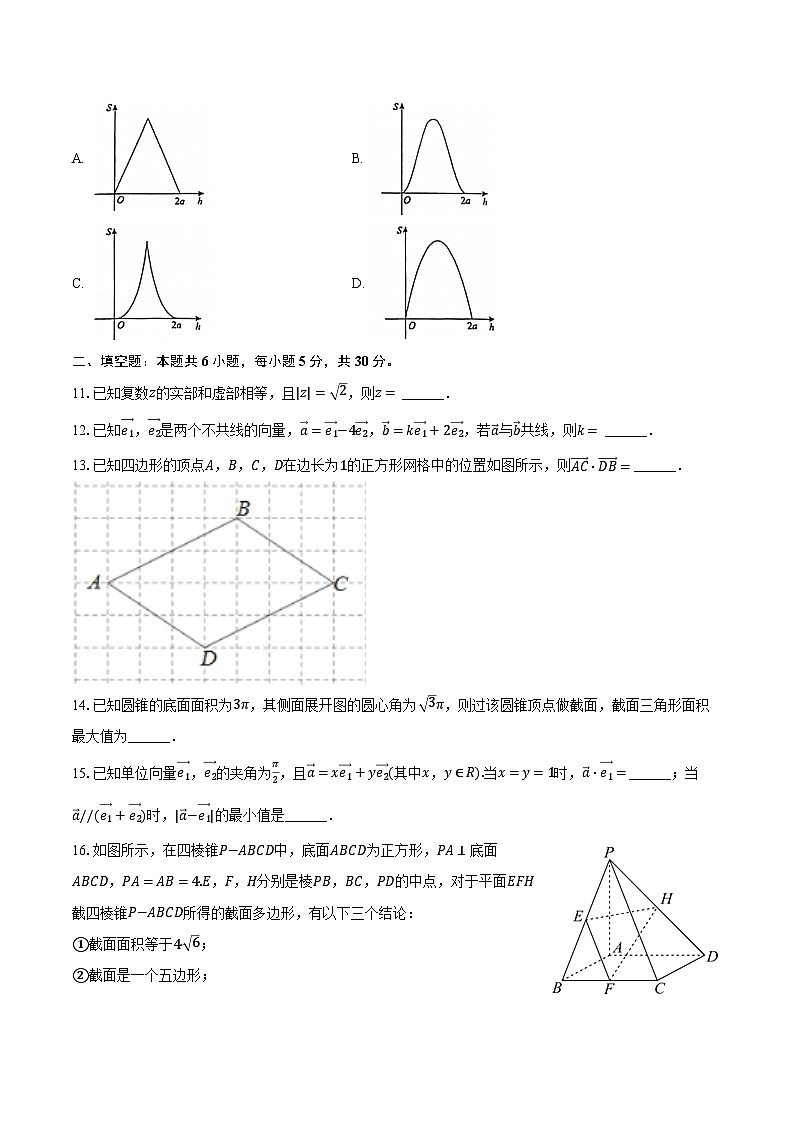
10.我国魏晋时期的数学家刘徽创造了一个称为“牟合方盖”的立体图形来推算球的体积，如图1，在一个棱长为2a的立方体内作两个互相垂直的内切圆柱，其相交的部分就是牟合方盖，如图2，设平行于水平面且与水平面距离为h的平面为a，记平面a截牟合方盖所得截面的面积为s，则函数S=f(h)的图象是( )
A. B.
C. D.
二、填空题：本题共6小题，每小题5分，共30分。
11.已知复数z的实部和虚部相等，且|z|= 2，则z= ______．
12.已知e1，e2是两个不共线的向量，a=e1−4e2，b=ke1+2e2，若a与b共线，则k= ______．
13.已知四边形的顶点A，B，C，D在边长为1的正方形网格中的位置如图所示，则AC⋅DB=______．
14.已知圆锥的底面面积为3π，其侧面展开图的圆心角为 3π，则过该圆锥顶点做截面，截面三角形面积最大值为______．
15.已知单位向量e1，e2的夹角为π2，且a=xe1+ye2(其中x，y∈R).当x=y=1时，a⋅e1=______；当a/​/(e1+e2)时，|a−e1|的最小值是______．
16.如图所示，在四棱锥P−ABCD中，底面ABCD为正方形，PA⊥底面ABCD，PA=AB=4.E，F，H分别是棱PB，BC，PD的中点，对于平面EFH截四棱锥P−ABCD所得的截面多边形，有以下三个结论：
①截面面积等于4 6；
②截面是一个五边形；
③直线PC与截面所在平面EFH无公共点．
其中，所有正确结论的序号是 ．
三、解答题：本题共5小题，共70分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题14分)
在锐角△ABC 中，角 A，B，C 所对的边分别为a，b，c，已知a= 7，b=3， 7sinB+sinA=2 3．
(Ⅰ) 求角A 的大小；
(Ⅱ) 求△ABC 的面积．
18.(本小题14分)
如图，在四棱锥P−ABCD中，底面ABCD是正方形，PA⊥平面ABCD，且
PA=AD=2，点E为线段PD的中点．
(Ⅰ)求证：PB/​/平面AEC；
(Ⅱ)求证：AE⊥平面PCD；
(Ⅲ)求三棱锥A−PCE的体积
19.(本小题14分)
在△ABC中，a=2,asinB+ 3bcsA=0．
(Ⅰ)求A；
(Ⅱ)除上述条件外，△ABC同时满足_____，求sinC的值；
请从①B=π4，②b=3，③3b=4sinA中选择一个符合题意的条件，补充到上面问题中，并完成解答．
(Ⅲ)求△ABC面积的最大值．
20.(本小题14分)
如图，已知正方体ABCD−A1B1C1D1的棱长为1，点E是棱AB上的动点，F是棱CC1上一点，CF：FC1=1：2．
(Ⅰ)求证：B1D1⊥A1F；
(Ⅱ)若直线A1F⊥平面B1D1E，试确定点E的位置，并证明你的结论；
(Ⅲ)设点P在正方体的上底面A1B1C1D1上运动，求总能使BP与A1F垂直的点P所形成的轨迹的长度．(直接写出答案)
21.(本小题14分)
n元向量(n−tuplevectr)也叫n维向量，是平面向量的推广，设n为正整数，数集P中的n个元素构成的有序组(a1,a2,⋯,an)称为P上的n元向量，其中ai(i=1,2,⋯,n)为该向量的第i个分量.n元向量通常用希腊字母α,β,γ等表示，如α=(a1,a2,⋯,an),P上全体n元向量构成的集合记为Pn.对于α,β∈Pn,n∈N*，记α=(a1,a2,⋯,an),β=(b1,b2,⋯,bn)，定义如下运算：加法法则α+β=(a1+b1,a2+b2,⋯,an+bn)，模公式||α||= i=1nai2= a12+a22+⋯+an2，内积α⋅β=i=1naibi=a1b1,a2b2,…,anbn，设α,β的夹角为θ，则csθ=α⋅β||α||⋅||β||．
(1)设α,β∈Pn,n≥3,n∈N*,α=(1,−1,1,1,⋯,1),β=(−1,1,1,⋯,1)，解决下面问题：
①求||α+β||；
②设α与α+β的夹角为θ，求csθ；
(2)对于一个n元向量α=(a1,a2,⋯,an)，若|ai|=1(i=1,2,⋯,n)，称α为n维信号向量.规定α⋅β=0⇔α⊥β，已知k个两两垂直的120维信号向量α1,α2,⋯,αk满足它们的前m个分量都相同，证明： km