§3.1　导数的概念及运算 课件-2025高考数学一轮复习

这是一份§3.1　导数的概念及运算 课件-2025高考数学一轮复习，共60页。PPT课件主要包含了落实主干知识，f′x0，αxα－1，cosx，－sinx，axlna，Cf′x，y′u·a，探究核心题型，命题点1求切线方程等内容，欢迎下载使用。
1.了解导数的概念、掌握基本初等函数的导数.2.通过函数图象，理解导数的几何意义.3.能够用导数公式和导数的运算法则求简单函数的导数，能求简单的复合函数的导数.
第一部分 落实主干知识
第二部分 探究核心题型
1.导数的概念(1)函数y＝f(x)在x＝x0处的导数记作 .
(2)函数y＝f(x)的导函数(简称导数)
2.导数的几何意义函数y＝f(x)在x＝x0处的导数的几何意义就是曲线y＝f(x)在点P(x0，f(x0))处的切线的　　　，相应的切线方程为　　　.
y－f(x0)＝f′(x0)(x－x0)
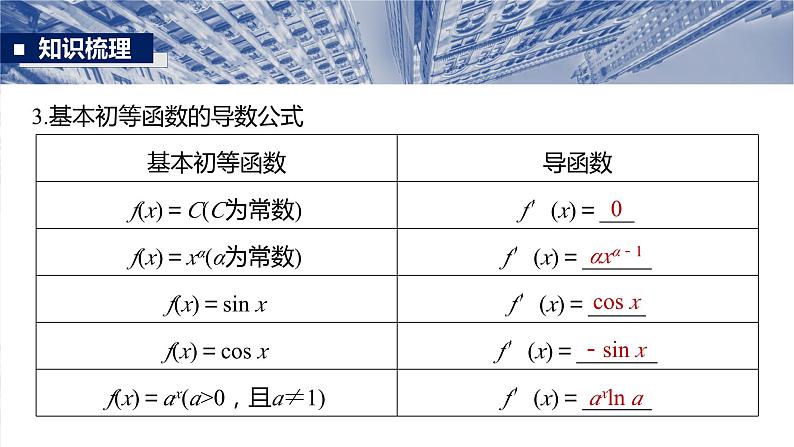
3.基本初等函数的导数公式
4.导数的运算法则若f′(x)，g′(x)存在，则有[f(x)±g(x)]′＝ ；[f(x)g(x)]′＝ ；
f′(x)±g′(x)
[Cf(x)]′＝ (C为常数).
f′(x)g(x)＋f(x)g′(x)
5.复合函数的定义及其导数一般地，对于两个函数y＝f(u)和u＝g(x)，如果通过中间变量u，y可以表示成x的函数，那么称这个函数为函数y＝f(u)和u＝g(x)的复合函数，记作y＝f(g(x)).一般地，我们有，若y＝f(u)，u＝ax＋b，则y′x＝y′u·u′x，即y′x＝________.
1.在点处的切线与过点的切线的区别(1)在点处的切线，该点一定是切点，切线有且仅有一条.(2)过点的切线，该点不一定是切点，切线至少有一条.
1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)f′(x0)是函数y＝f(x)在x＝x0附近的平均变化率.(　　)(2)与曲线只有一个公共点的直线一定是曲线的切线.(　　)(3)f′(x0)＝[f(x0)]′.(　　)(4)(e－x)′＝－e－x.(　　)
2.若函数f(x)＝3x＋sin 2x，则
4.设曲线y＝e2ax在点(0,1)处的切线与直线2x－y＋1＝0垂直，则a的值为 .
∵y＝e2ax，∴y′＝e2ax·(2ax)′＝2a·e2ax，∴在点(0,1)处的切线斜率k＝2ae0＝2a，又∵切线与直线2x－y＋1＝0垂直，
例1　(1)(多选)下列求导正确的是
对于A，[(3x＋5)3]′＝3(3x＋5)2(3x＋5)′＝9(3x＋5)2，故A正确；对于B，(x3ln x)′＝(x3)′ln x＋x3(ln x)′＝3x2ln x＋x2，故B正确；
(1)求函数的导数要准确地把函数拆分成基本初等函数的和、差、积、商，再利用运算法则求导.(2)抽象函数求导，恰当赋值是关键，然后活用方程思想求解.(3)复合函数求导，应由外到内逐层求导，必要时要进行换元.
跟踪训练1　(多选)下列命题正确的是A.若f(x)＝xsin x－cs x，则f′(x)＝sin x－xcs x＋sin xB.设函数f(x)＝xln x，若f′(x0)＝2，则x0＝eC.已知函数f(x)＝3x2ex，则f′(1)＝12e
对于选项A，f′(x)＝sin x＋xcs x＋sin x，故选项A不正确；对于选项B，f′(x)＝ln x＋1，则f′(x0)＝ln x0＋1＝2，解得x0＝e，故选项B正确；对于选项C，f′(x)＝6xex＋3x2ex，则f′(1)＝6e＋3e＝9e，故选项C不正确；
题型二　导数的几何意义
(2)(2022·新高考全国Ⅱ)曲线y＝ln|x|过坐标原点的两条切线的方程为 ， .
先求当x>0时，曲线y＝ln x过原点的切线方程，设切点为(x0，y0)，
解得y0＝1，代入y＝ln x，得x0＝e，
命题点2　求参数的值(范围)例3　(1)(2024·泸州模拟)若直线y＝kx＋1为曲线y＝ln x的一条切线，则实数k的值是
设直线y＝kx＋1在曲线y＝ln x上的切点为P(x0，y0)，
又切线方程为y＝kx＋1，
(2)(2022·新高考全国Ⅰ)若曲线y＝(x＋a)ex有两条过坐标原点的切线，则a的取值范围是 .
(－∞，－4)∪(0，＋∞)
因为y＝(x＋a)ex，所以y′＝(x＋a＋1)ex.
设切点为 ，O为坐标原点，
依题意得，切线斜率kOA＝ ，化简，得 ＋ax0－a＝0.因为曲线y＝(x＋a)ex有两条过坐标原点的切线，
所以Δ＝a2＋4a>0，解得a0，所以a的取值范围是(－∞，－4)∪(0，＋∞).
(1)处理与切线有关的问题，关键是根据曲线、切线、切点的三个关系列出参数的方程：①切点处的导数是切线的斜率；②切点在切线上；③切点在曲线上.(2)注意区分“在点P处的切线”与“过点P的切线”.
跟踪训练2　(1)(2023·深圳质检)已知f(x)为偶函数，当x0，g(x)单调递增；
当x∈　　　 时，g′(x)