2023-2024学年江苏省苏州市姑苏区七年级（上）期中数学试卷（含解析）

这是一份2023-2024学年江苏省苏州市姑苏区七年级（上）期中数学试卷（含解析），共12页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
1.−3的相反数是( )
A. 3B. −3C. 0D. ±3
2.数轴上的点A表示的数是
( )
A. 145000000B. 150000000C. 155000000D. 160000000
3.有一个长35cm，宽20cm，高15cm的长方体物体，它可能是( )
A. 铅笔盒B. 数学课本C. 书橱D. 鞋盒
4.有理数−2，−−32，−32，−2中，负数的个数是
( )
A. 1B. 2C. 3D. 4
5.今年小丽a岁，张老师年龄比小丽年龄的3倍小2岁，5年后，张老师年龄是
( )
A. a+5岁B. 3a+3岁C. 3a+5岁D. 3a−2岁
6.在课外兴趣小组活动中，小明对制作的行走机器人进行5分钟行走测试．若机器人第1分钟行走2m，从第2分钟起每分钟的行走路程是前一分钟的2倍，则机器人在第5分钟行走的路程是
( )
A. 16mB. 32mC. 64mD. 128m
7.三条线段恰好可以围成一个三角形，其中两条线段的长度分别为7cm，11cm，则第三条线段的长度不可能是
( )
A. 3cmB. 7cmC. 11cmD. 15cm
8.如图，数轴上点A，B，C分别表示非零有理数a，b，c，若a+b+c=c−a−b，那么数轴的原点应该在
( )
A. 点A左边B. 点A和点B之间C. 点B和点C之间D. 点C右边
9.如图，正方形的边长为a，将它的边长增加3得到一个新的正方形，增加的面积用代数式表示为
( )
A. 3a×2B. a+3×3C. a+3×3×2D. a+32−a2
10.我国是历史上较早发现并运用“勾股定理”的国家之一，“勾股定理”描述了直角三角形三条边长之间的关系：直角三角形两直角边的平方和等于斜边的平方，请运用“勾股定理”解决以下问题：如图，一个底面半径为8cm，高为15cm的圆柱形饮料罐，将一根笔直的吸管从顶面正中的小圆孔插入饮料罐，若罐壁厚度和顶部圆孔直径均忽略不计，则吸管在饮料罐内部的最大长度是
( )
A. 16cmB. 17cmC. 20cmD. 25cm
二、填空题：本题共8小题，每小题3分，共24分。
11.大于−2.6小于3.1的整数有______个．
12.统计数据显示，2023年“十一”黄金周期间，苏州全市70家重点监测商贸企业累计实现零售额16.7亿元，数据“1670000000”用科学记数法表示为______．
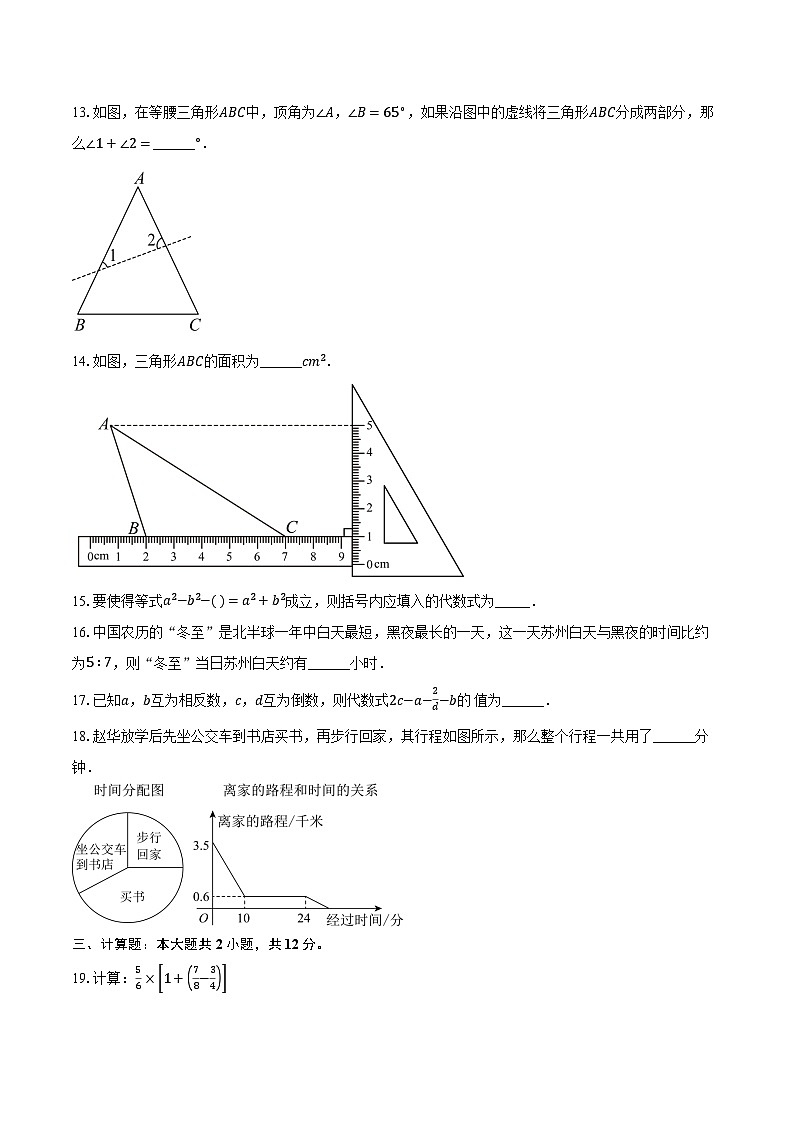
13.如图，在等腰三角形ABC中，顶角为∠A，∠B=65∘，如果沿图中的虚线将三角形ABC分成两部分，那么∠1+∠2=______°．
14.如图，三角形ABC的面积为______cm2．
15.要使得等式a2−b2− =a2+b2成立，则括号内应填入的代数式为_____．
16.中国农历的“冬至”是北半球一年中白天最短，黑夜最长的一天，这一天苏州白天与黑夜的时间比约为5∶7，则“冬至”当日苏州白天约有______小时．
17.已知a，b互为相反数，c，d互为倒数，则代数式2c−a−2d−b的 值为______．
18.赵华放学后先坐公交车到书店买书，再步行回家，其行程如图所示，那么整个行程一共用了______分钟．
三、计算题：本大题共2小题，共12分。
19.计算：56×1+78−34
20.计算：−23×−32+98−12−32
四、解答题：本题共3小题，共24分。解答应写出文字说明，证明过程或演算步骤。
21.(本小题8分)
探究与发现：
(1)如图①，四个小长方形拼成一个大长方形，点P在线段AC上，试判断长方形EPHD与长方形GBFP面积的大小关系，并简单说明理由；
(2)如图②，长方形GBFP的顶点P在直角三角形ABC的斜边AC上，若AG=50，FC=75，利用第(1)小题的探究方法和结论，求长方形GBFP的面积．
22.(本小题8分)
互不相等的有理数m，n，p在数轴上分别表示点M，N，P，若MP=PN=r，则称有理数m和n关于p对称，对称半径为r，例如：有理数3和5关于4对称，对称半径为1．
(1)若有理数3和x关于1对称，则x=______；对称半径r=______；
(2)若有理数a和b关于2对称，且a=2b，求对称半径r．
23.(本小题8分)
某中学科学社团进行课外实验，在桌上有一段笔直的轨道AB，长度为10cm的金属滑块在上面做往返滑动．如图，滑块首先沿AB方向从左向右匀速滑动，滑动速度为acm/s，滑动开始前滑块左端与点A重合，当滑块右端到达点B时，滑块停顿2s，然后再以bcm/s的速度匀速返回，直到滑块的左端与点A重合，滑动停止，设时间为ts时，滑块左端离点A的距离为l1cm，离点B的距离为l2cm，记k=l1l2，已知0≤k≤9，滑块从点A出发最后返回点A，整个过程总用时62s(含停顿时间)，请你根据所给条件解决下列问题：
(1)滑块从点A到点B的滑动过程中，k的值____________；(填“由大到小”或“由小到大”)
(2)若a=b，当t=20时，求k的值；
(3)若a=2b，在整个往返过程中，求使得k=1时t的值．
答案和解析
1.【答案】A
【解析】【分析】只有符号不同的两个数互为相反数，根据概念即可完成．
【详解】只有符号不同的两个数互为相反数
−3的相反数是3
故选A
本题考查相反数的概念，熟练掌握该知识点是解题关键．
2.【答案】C
【解析】【分析】本题考查了数轴的知识点，熟练掌握以上知识点是解题的关键．
【 详解】解：根据题意得A=1.55亿，
即A表示的数是155000000．
故选：C．
3.【答案】D
【解析】【分析】本题主要考查几何体的认识，解题的关键是理解题意；所以此题可根据题意结合实际生活可进行求解．
【详解】解：∵铅笔盒和数学课本的高度达不到15cm，故选项A，B可以排除；
又∵书橱的高度大于15cm，故选项C可以排除．
故选：D．
4.【答案】C
【解析】【分析】本题主要考查了负数的概念和绝对值的代数意义；准确化简绝对值并理解负数的概念及是解题关键．根据负数的定义，可知−−32，−32，−2为负数，从而选出正确选项．
【详解】解：根据负数的定义，
∴ −−32，−32，−2为负数；
故选：C．
5.【答案】B
【解析】【分析】本题考查了列代数式，根据题意找出关系式是解题关键．
【详解】解：因为今年小丽a岁，张老师年龄比小丽年龄的3倍小2岁，
所以5年后，张老师年龄是3a−2+5=3a+3岁；
故选：B．
6.【答案】B
【解析】【分析】本题主要考查有理数乘方的应用，熟练掌握有理数的乘方是解题的关键．
【详解】解：由题意得：第5分钟行走的路程是25=32m．
故选：B．
7.【答案】A
【解析】【分析】本题考查了三角形的三边关系．根据三角形的三边关系即可判断第三边的取值范围，熟练掌握三角形任意两边之和大于第三边，两边之差小于第三边是解此题的关键．
【详解】解：设第三根木棒的长度为xcm，
∴11−7