2024年中考数学复习课件---第22讲 圆及其基本性质

这是一份2024年中考数学复习课件---第22讲 圆及其基本性质，共41页。PPT课件主要包含了栏目导航，圆及其基本性质，圆的定义，确定圆的条件，圆的性质，垂径定理及其推论，垂径定理，垂径定理的应用，三角形的外接圆，圆内接四边形的性质等内容，欢迎下载使用。

1.理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念；探 索并掌握点与圆的位置关系。2.探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧。3.探索圆周角与圆心角及其所对弧的关系，知道同弧(或等弧)所对的圆周 角相等。了解并证明圆周角定理及其推论:圆周角等于它所对弧上的 心角的一半；直径所对的圆周角是直角；90°的圆周角所对的弦是直径； 圆内接四边形的对角互补。4.了解三角形的外心。5.了解正多边形的概念及正多边形与圆的关系。
教材链接人教：九上P78~P91、P105~P110北师：九下P65~P84、P97~P99湘教：九下P43~P60、P83~P86
弦、弧、圆心角、圆周角
弧、弦、圆心角之间的关系
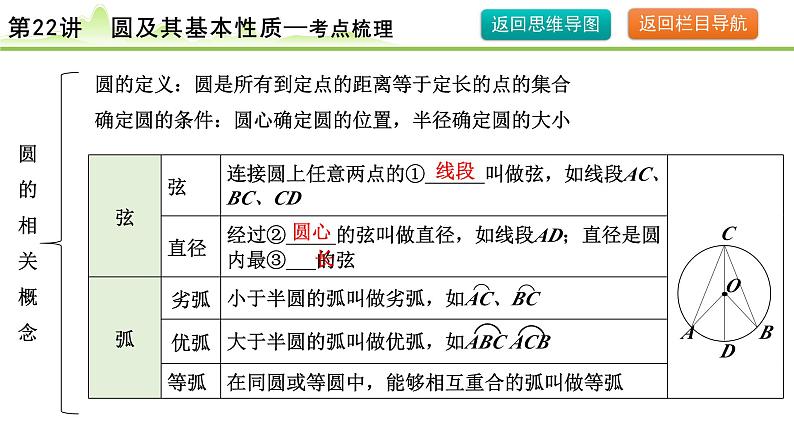
圆的定义：圆是所有到定点的距离等于定长的点的集合确定圆的条件：圆心确定圆的位置，半径确定圆的大小
轴对称性：圆是轴对称图形，任何一条⑥______所在的直线都 中心对称性：圆是中心对称图形，对称中心是⑦________旋转不变性：圆绕着它的圆心旋转任意角度，都能与原来的图
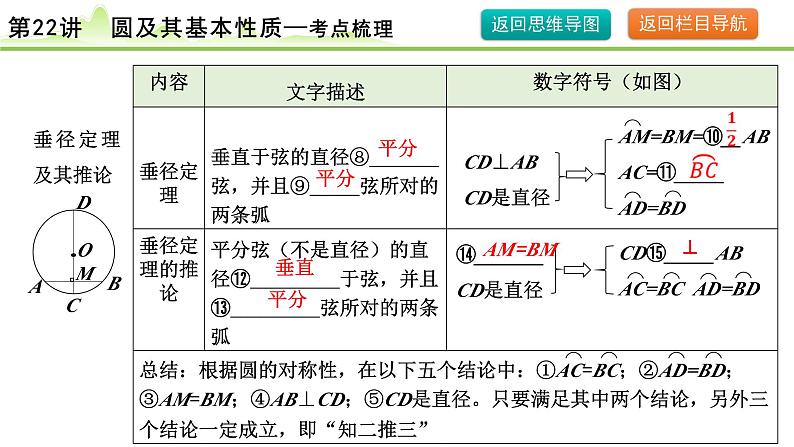
AM=BM=⑩__ABAC=⑪_____AD=BD
⑭_______CD是直径
CD⑮_____ABAC=BC AD=BD
【易错提示】在使用垂径定理的推论时注意“弦非直径”这一条件，因 为所有的直径互相平分，但互相平分的直径不一定垂直. 
【易错提示】（1）一条弦对着两条弧，这两条弧所对的圆周角互补； （2）一条弧只对着一个圆心角，但却对着无数个圆周角。 
定义：经过三角形的三个顶点可以作一个圆，这个圆叫做三角形的外接圆圆心O名称：外心（即三角形三条边的㊱____________的交点）性质：三角形的外心到三角形㊲______________________角度关系：∠BOC=2=∠A
（1）圆内接四边形的对角互补，如图，∠A+∠BCD=㊳_________，∠B+∠D=㊴_________（2）圆内接四边形的任意一个角的外角等于它的内对角，如图，∠DCE=㊵___________
例 原创题 如图,AB为☉O的直径,C,D为☉O上的两点,连接CD交AB 于点E.
(1)如图1,连接CO,若∠ABD=46°,∠AEC=58°,则∠AOC的度数____; 
(2)在(1)的条件下,若DC=4,求AB的长度;
(4)在(3)的条件下,若DB=3,DH=5,求FH的长.
方法指导1.圆中通常将圆周角和圆心角以及它们所对的弧的度数进行转换,常用同弧(或等弧)所对的圆周角等于圆心角的一半来转换.2.当出现直径时,常构造直径所对的圆周角是直角来进行证明或计算.3.根据半径相等构造等腰三角形,利用等边对等角以及“三线合一”来进行证明和计算.
1.(2022·毕节模拟)如图,已知CD为☉O的直径,过点D的弦DE平行 于半径OA,若∠D的度数是50°,则∠C的度数是 (　　) A.50°　　 B.40°　　 C.30°　　 D.25°
2.(2022·铜仁石阡县模拟)如图,在平面直角坐标系中,☉M经过原 点,且与x轴交于点A(4,0),与y轴交于点B,点C在第四象限的☉M 上,且∠AOC=60°,OC=3,则点B的坐标是　　　　. 
3.(2022·贵阳南明区模拟)已知:如图,△ABC内接于☉O,AB为直 径,∠CBA的平分线交AC于点F,交☉O于点D,DE⊥AB于点E,且交 AC于点P,连接AD.
(1)求证:∠DAC=∠DBA;(2)求证:P是线段AF的中点;
证明:∵BD平分∠CBA,∴∠CBD=∠DBA.∵∠DAC=∠CBD,∴∠DAC=∠DBA.
(3)连接CD,若CD=3,BD=4,求☉O的半径和DE的长.
解:如图,连接CD.∵∠CBD=∠DBA,∴CD=AD.∵CD=3,∴AD=3.∵∠ADB=90°,∴AB=5.∴☉O的半径为2.5.∵DE×AB=AD×BD,∴5DE=3×4.∴DE=2.4,即DE的长为2.4.
（2017~2022）
2.(2022·遵义15题4分)数学小组研究如下问题:遵义市某地的纬度约 为北纬28°,求北纬28°纬线的长度. 小组成员查阅相关资料,得到如下信息:
信息一:如图1,在地球仪上,与赤道平行的圆圈叫做纬线;信息二:如图2,赤道半径OA约为6 400千米,弦BC∥OA,以BC为直径的圆的周长就是北纬28°纬线的长度;
(参考数据:π≈3,sin28°≈0.47,cs28°≈0.88,tan28°≈0.53)根据以上信息,北纬28°纬线的长度约为　　　　千米. 
4.(2020·遵义16题4分)如图,☉O是△ABC的外接圆,∠BAC=45°, AD⊥BC于点D,延长AD交☉O于点E,若BD=4,CD=1,则 DE的长是　　　　. 
(贵阳6年2考,遵义6年3考,毕节6年
5.(2018·铜仁5题4分)如图,已知圆心角∠AOB=110°,则圆周角 ∠ACB=(　　) A.55°　　 B.110°　　 C.120°　　 D.125°
7.(2019·铜仁13题4分)如图,四边形ABCD为☉O的内接四边形, ∠A=100°,则∠DCE的度数为　　　　.
8.(2018·毕节19题5分)如图,AB是☉O的直径,C,D为半圆的三等分点, CE⊥AB于点E,∠ACE的度数为　　　　. 
9.(2020·贵阳14题4分)如图,△ABC是☉O的内接正三角形,点O是圆心, 点D,E分别在边AC,AB上,若DA=EB,则∠DOE的度数是__________。 
10.(2021·毕节24题12分)如图,☉O是△ABC的外接圆,点E是△ABC的 内心,AE的延长线交BC于点F,交☉O于点D,连接BD,BE. (1)求证:DB=DE; (2)若AE=3,DF=4,求DB的长.
(1)求证:DB=DE;
(2)若AE=3,DF=4,求DB的长.
11.(2019·贵阳6题3分)如图,正六边形ABCDEF内接于☉O,连 接BD,则∠CBD的度数是(　　) A.30°　 B.45°　 C.60°　 D.90°
12.(2021·贵阳9题3分)如图,☉O与正五边形ABCDE的两边 AE,CD相切于A,C两点,则∠AOC的度数是(　　) A.144°　 B.130°　 C.129°　 D.108°