初中数学人教版九年级下册26.1.1 反比例函数课时练习

这是一份初中数学人教版九年级下册26.1.1 反比例函数课时练习，文件包含2612反比例函数的图像和性质讲+练12大题型原卷版docx、2612反比例函数的图像和性质讲+练12大题型解析版docx等2份试卷配套教学资源，其中试卷共58页， 欢迎下载使用。

一、单选题
1．如图，点A为反比例函数y=﹣ 4x 图象上一点，过点A作AB⊥x轴于点B，连结OA，则△ABO的面积为（ ）
A．16B．8C．4D．2
2．已知（－2，y1），（－1，y2），（1，y3）都在反比例函数上 y=1x 的图象上.下列结论正确的是（ ）
A．y3>y1>y2B．y1>y3>y2C．y1>y2>y3D．y3>y2>y1
3．已知点P（1，﹣3）在反比例函数y= kx （k≠0）的图象上，则k的值是（ ）
A．3B．﹣3C．13D．﹣ 13
4．下列函数中，当 x>0 时，y随x增大而减小的是（ ）
A．y=x2B．y=x−1C．y=34xD．y=−x2
5．已知抛物线 y=x2+2x−m−2 与x轴没有交点，则函数 y=mx 的大致图象是（ ）
A．B．
C．D．
6．一次函数y=ax+a（a为常数，a≠0）与反比例函数y= ax （a为常数，a≠0）在同一平面直角坐标系内的图象大致为（ ）
A．B．
C．D．
二、填空题
7．A、B两地相距120千米，一辆汽车从A地去B地，则其速度v（千米/时）与行驶时间t（小时）之间的函数关系可表示为 ；
8．已知反比例函数y=−6x的图象经过点(4，a)，则a的值为 ．
9．如图，在平面直角坐标中，一次函数y＝﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的顶点C、D在第一象限，顶点D在反比例函数 y=kx （k≠0）的图象上.若正方形ABCD向左平移n个单位后，顶点C恰好落在反比例函数的图象上，则n的值是 .
10．如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为4，2，反比例函数y＝ kx (x＞0)的图象经过A，B两点，若菱形ABCD的面积为2 5 ，则k的值为 .
三、作图题
11．已知反比例函数 y=kx 的图象与正比例函数 y=2x 的图象交于点 (2,m) ，求这个反比例函数的表达式，并在同一平面直角坐标系内，画出这两个函数的图象．
四、解答题
12．已知反比例函数 y=m−5x 的图象过点P（－1，3），求m的值和该反比例函数的表达式.
13．已知y是x的反比例函数，且x=8时，y=12．写出y与x之间的函数关系式；
14．公司员工甲去距离单位6千米的社区医院接种新冠疫苗，去时骑自行车，在医院等候和接种疫苗花了2小时，回来时发现时间可能来不及了，改乘汽车返回公司，已知其骑自行车的速度不超过 15km/ℎ ，汽车的速度是骑自行速度的1.5倍，并且公司规定在离开之时算起2.5小时内需返回公司.问甲能否规定时间内及时返回公司？
15．如图，一次函数的图象与反比例函数的图象相交于 A ， B 两点，与 y 轴的正半轴相交于点 C ，与 x 轴的负半轴交于点 D ， OB=5 ， tan∠DOB=12 ．
（1）求反比例的表达式；
（2）若点 A 的横坐标为 23 ，求 △AOC 的面积．
反比例函数的图象特征：
反比例函数的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限或第二、四象限；反比例函数的图象关于原点对称，永远不会与轴、轴相交，只是无限靠近两坐标轴.
注意：（1）若点()在反比例函数的图象上，则点()也在此图象上，所以反比例函数的图象关于原点对称；
（2）在反比例函数(为常数，) 中，由于，所以两个分支都无限接近但永远不能达到轴和轴．
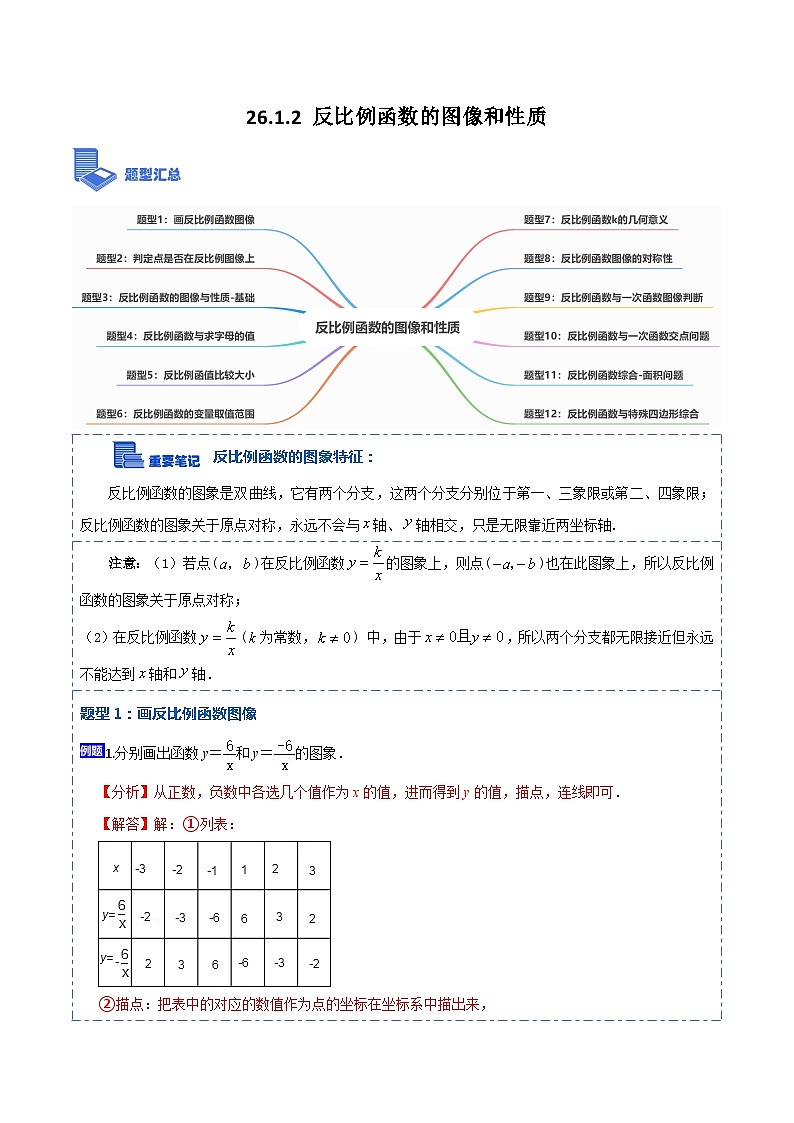
题型1：画反比例函数图像
1.分别画出函数y＝和y＝的图象．
【变式1-1】用描点法画出反比例函数y＝和y＝﹣的图象．
（1）列表：
x
…
…
y＝
…
…
y＝﹣
…
…
（2）在如图坐标系中描点，并用光滑曲线顺次连结各点．
【变式1-2】已知函数y＝（m﹣2）x是反比例函数．
（1）求m的值；
（2）画出函数的图象．
题型2：判定点是否在反比例图像上
2.反比例函数y＝（k≠0）经过点（﹣1，4），则下列各点也在这个函数图象上的是（ ）
A．（﹣1，﹣4）B．（1，4）C．（﹣2，﹣2）D．（2，﹣2）
【变式2-1】已知反比例函数y＝（k常数，k≠1）．
（1）若点A（1，﹣2）在这个函数的图象上，求k的值；
（2）若k＝5，试判断点B（﹣，﹣8）是否在这个函数的图象上，并说明理由．
【变式2-2】反比例函数y＝的图象过A（2，3）．
（1）求这个函数解析式；
（2）点（﹣1，m）在函数图象上，求m值；
（3）判断B（1，6）是否在函数图象上？C（﹣2，3）呢？
反比例函数的性质
（1）如图1，当时，双曲线的两个分支分别位于第一、三象限，在每个象限内，值随值的增大而减小；
（2）如图2，当时，双曲线的两个分支分别位于第二、四象限，在每个象限内，值随值的增大而增大；
注意：反比例函数的增减性不是连续的，它的增减性都是在各自的象限内的增减情况，反比例函数的增减性都是由反比例系数的符号决定的；反过来，由双曲线所在的位置和函数的增减性，也可以推断出的符号.
题型3：反比例函数的图像与性质-基础
3.下列函数：①y＝﹣5x；②y＝3x﹣2；③y＝﹣（x＞0）；④y＝3x2（x＜0），其中y的值随x的增大而增大的函数为 .（填序号）
【变式3-1】已知函数的图象位于第二、第四象限，则k的取值范围为 ．
【变式3-2】已知反比例函数y＝，分别根据下列条件求出字母k的取值范围．
（1）函数的图象位于一、三象限；
（2）在第二象限内，y随x的增大而增大．
题型4：反比例函数与求字母的值
4.设y＝（2n+1）x
（1）当n为何值时，y与x是正比例函数，且图象经过一、三象限；
（2）当n为何值时，y与x是反比例函数，且在每个象限内y随着x的增大而增大．
【变式4-1】已知反比例函数y＝（m﹣2）
（1）若它的图象位于第一、三象限，求m的值；
（2）若它的图象在每一象限内y的值随x值的增大而增大，求m的值．
【变式4-2】已知反比例函数y＝（m﹣2）．
（1）当反比例函数的图象位于第一、三象限时，求m的值？
（2）当反比例函数的图象位于第二、四象限时，求m的值？
题型5：反比例函值比较大小
5.已知点（4，y1），（6，y2），在反比例函数的图象上，则y1，y2的大小关系为（ ）
A．y1＞y2B．y1＜y2C．y1＝y2D．无法判断
【变式5-1】若点A（﹣3，y1），B（﹣2，y2），C（3，y3）在反比例函数的图象上，则y1，y2，y3大小关系是（ ）
A．y1＜y2＜y3B．y1＜y3＜y2C．y2＜y1＜y3D．y3＜y1＜y2
【变式5-2】点A（x1，y1），B（x2，y2），C（x3，y3）都在反比例函数y＝的图象上，若x1＜x2＜0＜x3，则y1，y2，y3大小关系是 （用“＜”连接）
题型6：反比例函数的变量取值范围
6.已知y是x的反比例函数，且x＝3时，y＝8．
（1）写出y与x之间的函数关系式；
（2）如果自变量x的取值范围为3≤x≤4．求y的取值范围．
【变式6-1】若函数y＝（m﹣2）是y关于x的反比例函数．
（1）求m的值；
（2）函数图象在哪些象限？在每个象限内，y随x的增大而怎样变化？
（3）当﹣3≤x≤﹣时，求y的取值范围．
【变式6-2】作出函数y＝的图象，并根据图象回答下列问题：
（1）当x＝﹣2时，求y的值；
（2）当2＜y＜3时，求x的取值范围；
（3）当﹣4＜x＜﹣2时，求y的取值范围．
【变式6-3】设函数y＝﹣．
（1）画出函数的图象；
（2）利用图象求﹣3≤x≤﹣1时，函数值y的变化范围；
（3）当3≤x≤6时，函数的最大值和最小值各是多少？
反比例函数()中的比例系数k的几何意义
过双曲线() 上任意一点作轴、轴的垂线，所得矩形的面积为.
过双曲线() 上任意一点作一坐标轴的垂线，连接该点和原点，所得三角形的面积为.
注意：只要函数式已经确定，不论图象上点的位置如何变化，这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的.
题型7：反比例函数k的几何意义
7.如图，点A在双曲线上，AB⊥x轴于B，且△AOB的面积S△AOB＝2，则k的值为（ ）
A．2B．4C．﹣2D．﹣4
【变式7-1】若图中反比例函数的表达式均为，则阴影面积为2的是（ ）
A．B．
C．D．
【变式7-2】如图，点A，B关于y轴对称，S△AOB＝8，点A在双曲线y＝上，求k的值．
题型8：反比例函数图像的对称性
8.正比例函数y＝2x和反比例函数的一个交点为（1，2），则另一个交点为（ ）
A．（﹣1，﹣2）B．（﹣2，﹣1）C．（1，2）D．（2，1）
【变式8-1】如图，正比例函数与反比例函数的图象相交于AB、两点，分别以AB、两点为圆心，画与x轴相切的两个圆，若点A的坐标为（2，1），则图中两个阴影部分面积的和是（ ）
A．B．C．πD．4π
【变式8-2】如图，点P（﹣2a，a）是反比例函数y＝的图象与⊙O的一个交点，图中阴影部分的面积为10π，则该反比例函数的表达式为（ ）
A．y＝﹣B．y＝﹣C．y＝﹣D．y＝﹣
【变式8-3】边长为4的正方形ABCD的对称中心是坐标原点O，AB∥x轴，BC∥y轴，反比例函数y＝与y＝﹣的图象均与正方形ABCD的边相交，则图中的阴影部分的面积是（ ）
A．2B．4C．8D．6
题型9：反比例函数与一次函数图像判断
9.函数和y＝﹣kx+2（k≠0）在同一平面直角坐标系中的大致图象可能是（ ）
A．B．
C．D．
【变式9-1】在同一平面直角坐标系中，函数y＝ax+b与（其中a，b是常数，ab≠0）的大致图象是（ ）
A．B．
C．D．
【变式9-2】在同一平面直角坐标系中，函数y＝kx﹣k与y＝（k＜0）的图象大致是（ ）
A．B．
C．D．
题型10：反比例函数与一次函数交点问题
10.如图，正比例函数y＝2x的图象与反比例函数y＝的图象有一个交点为P（2，m）．
（1）求反比例函数y＝函数表达式；
（2）根据图象，直接写出当﹣4＜x＜﹣1时，反比例函数y＝的y取值范围．
【变式10-1】如图，直线y1＝k1x+b与双曲线y2＝相交于A（1，2）、B（m，﹣1）两点．
（1）求直线和双曲线的表达式；
（2）根据图象，直接写出满足关于x的不等式k1x+b＜的解集．
【变式10-2】已知反比例函数y1＝与一次函数y2＝2x+k（k是常数），它们的图象有一个交点A，点A的横坐标是﹣2．
（1）求k的值．
（2）当y1＜y2＜0时，求x的取值范围．
题型11：反比例函数综合-面积问题
11.如图，在平面直角坐标系中，直线y＝x+3与双曲线y＝交于A，B两点，已知点A的横坐标为2．
（1）求k的值；
（2）求△OAB的面积；
（3）直接写出关于x的不等式x+3的解集．
【变式11-1】如图，一次函数y＝mx+n（m≠0，m，n是常数）与反比例函数y＝（k≠0）在第二象限的图象交于点A（﹣1，a），B两点，与x轴、y轴分别交于点C、点D，且OC＝OD＝3．
（1）求反比例函数的解析式；
（2）连接OA，求△AOC的面积．
【变式11-2】如图，在平面直角坐标系中，一次函数y＝k1x+b（k1≠0）的图象与反比例函数y＝（k2≠0）的图象交于点A（a，2），B（﹣1，﹣8）．
（1）求一次函数和反比例函数的表达式；
（2）请根据函数图象直接写出关于x的不等式k1x+b≤的解；
（3）连接OA，OB，求△AOB的面积．
题型12：反比例函数与特殊四边形综合
12.如图，在平面直角坐标系中，平行四边形OABC的边OC在x轴上，对角线AC，OB交于点M，点B（12，4）．若反比例函数的图象经过A，M两点，求：
（1）点M的坐标及反比例函数的解析式；
（2）△AOM的面积；
（3）平行四边形OABC的周长．
【变式12-1】如图，在以O为原点的平面直角坐标系中，点A、C分别在x轴、y轴的正半轴上，点B（a，b）在第一象限，四边形OABC是矩形，反比例函数的图象与AB相交于点D，与BC相交于点E，且BE＝2CE．
（1）求证：BD＝2AD；
（2）若四边形ODBE的面积是6，求k的值．
【变式12-2】如图，B（﹣1，0），正方形ABCD中心为O1，双曲线y＝正好经过C、O1两点，求k的值．