备战中考数学《重难点解读•专项训练》专题01 辅助圆定点定长（知识解读）

这是一份备战中考数学《重难点解读•专项训练》专题01 辅助圆定点定长（知识解读），共13页。试卷主要包含了复习方法，复习难点等内容，欢迎下载使用。

一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度，培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准，安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础，在此基础上适当增加变式和难度，提高能力。
专题01 辅助圆定点定长（知识解读）
【专题说明】
最值问题的必要条件是至少有一个动点，因为是动态问题，所以才
会有最值。初中阶段动点的运动轨迹主要是“一条直线”或“圆”。在这类题目中，题目很少直接告诉我们动点轨迹是个圆，也很少把这个圆画出来，因此，结合题目给的条件，分析出动点的轨迹图形，将是我们面临的最大的问题。
【方法技巧】
模型一：定点定长作圆
点A为定点，点B为动点，且AB长度固定，
则点B的轨迹是以点A为圆心，AB长为半径的圆。
模型一：点圆最值
已知平面内一定点D和O，点E是O上一动点，设点O与点D之间距离为d，O半径为r.
【典例分析】
【典例1】如图，在四边形ABCD中，AB＝AC＝AD，∠CAD＝2∠BAC，若∠BCD＝105°，则∠BDC＝ ．
版权所
【变式1】如图，在四边形ABCD中，90°＜∠BAD＜180°，AB＝AC＝AD，请画出满足条件时点C的轨迹．
【典例2】如图，在△ABC中，点D是边BC的中点，点E是边AC上的任意一点（点E不与点C重合），沿DE翻折△DCE使点C落在点F处，请画出点F的轨迹．
【变式2】如图，在▱ABCD中，AE⊥BC于点E，将△AEB绕点B顺时针旋转，使AB与边BC重合，得到△MNB，请画出在旋转过程中点M的运动轨迹．
【典例3】如图，在矩形ABCD中，，，E是AB边的中点，F是线面BC边上的动点，将沿EF所在的直线折叠得到，连接，求的最小值。

【变式3-1】（2019•锦州）如图，在矩形ABCD中，AB＝3，BC＝2，M是AD边的中点，N是AB边上的动点，将△AMN沿MN所在直线折叠，得到△A′MN，连接A′C，则A′C的最小值是 ．
【变式3-2】如图，矩形ABCD中，AB＝4，BC＝8，P是直线AB上的一个动点，AE＝2，△APE沿PE翻折形成△FPE，连接PF、EF，则FC的最小值是 ，点F到线段BC的最短距离是 ．
【典例4】（2021秋•邗江区期末）如图，在平面直角坐标系xOy中，已知点A（1，0），B（3，0），C为平面内的动点，且满足∠ACB＝90°，D为直线y＝x上的动点，则线段CD长的最小值为（ ）
A．1B．2C．D．
【变式4-1】（2021秋•武江区校级期末）如图，⊙M的半径为4，圆心M的坐标为（5，12），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为 ．
【变式4-2】（2021秋•萨尔图区校级期末）如图，点A，B的坐标分别为A（4，0），B（0，4），C为坐标平面内一点，BC＝2，点M为线段AC的中点，连接OM，OM的最大值为 ．
专题01 辅助圆定点定长（知识解读）
【专题说明】
最值问题的必要条件是至少有一个动点，因为是动态问题，所以才
会有最值。初中阶段动点的运动轨迹主要是“一条直线”或“圆”。在这类题目中，题目很少直接告诉我们动点轨迹是个圆，也很少把这个圆画出来，因此，结合题目给的条件，分析出动点的轨迹图形，将是我们面临的最大的问题。
【方法技巧】
模型一：定点定长作圆
点A为定点，点B为动点，且AB长度固定，
则点B的轨迹是以点A为圆心，AB长为半径的圆。
模型一：点圆最值
已知平面内一定点D和O，点E是O上一动点，设点O与点D之间距离为d，O半径为r.
【典例分析】
【典例1】如图，在四边形ABCD中，AB＝AC＝AD，∠CAD＝2∠BAC，若∠BCD＝105°，则∠BDC＝ ．
【解答】解：以A为圆心，AB为半径画圆，
∴∠CAD＝2∠CBD，∠BAC＝2∠BDC，
∵∠CAD＝2∠BAC，
∴∠CBD＝2∠BDC，
∵∠CBD+∠BDC+∠BCD＝180°，
∴3∠CBD+105°＝180°，
∴∠CBD＝25°．
故答案为：25°．

【变式1】如图，在四边形ABCD中，90°＜∠BAD＜180°，AB＝AC＝AD，请画出满足条件时点C的轨迹．
【解答】解：∵AB＝AC＝AD，
∴点C在以A为圆心，AB为半径的圆上运动，
∵四边形ABCD中，90°＜∠BAD＜180°，
∴点C的运动轨迹为（不与B、D重合）．
【典例2】如图，在△ABC中，点D是边BC的中点，点E是边AC上的任意一点（点E不与点C重合），沿DE翻折△DCE使点C落在点F处，请画出点F的轨迹．
【解答】解：∵DF＝DC，
∴则点F在以点D为圆心DC为半径的圆上运动，
当点E与A重合时，AD与⊙D交于Q，
则即为点F的运动轨迹．
∠FDE＝∠CDE＝∠CDA，则轨迹为优弧MQC，满足∠MDA＝∠CDA，
此时点F的轨迹为．
【变式2】如图，在▱ABCD中，AE⊥BC于点E，将△AEB绕点B顺时针旋转，使AB与边BC重合，得到△MNB，请画出在旋转过程中点M的运动轨迹．
【解答】解：如图，弧AM即为所求．
【典例3】如图，在矩形ABCD中，，，E是AB边的中点，F是线面BC边上的动点，将沿EF所在的直线折叠得到，连接，求的最小值。
解：如图，点E为圆心，为半径作圆，
当点E，，D三点共线时的值最小。
，，
，

【变式3-1】（2019•锦州）如图，在矩形ABCD中，AB＝3，BC＝2，M是AD边的中点，N是AB边上的动点，将△AMN沿MN所在直线折叠，得到△A′MN，连接A′C，则A′C的最小值是 ．
【考点】翻折变换（折叠问题）；矩形的性质．
【解答】解：∵四边形ABCD是矩形
∴AB＝CD＝3，BC＝AD＝2，
∵M是AD边的中点，
∴AM＝MD＝1
∵将△AMN沿MN所在直线折叠，
∴AM＝A'M＝1
∴点A'在以点M为圆心，AM为半径的圆上，
∴如图，当点A'在线段MC上时，A'C有最小值，
∵MC＝＝
∴A′C的最小值＝MC﹣MA'＝﹣1
故答案为：﹣1
【变式3-2】如图，矩形ABCD中，AB＝4，BC＝8，P是直线AB上的一个动点，AE＝2，△APE沿PE翻折形成△FPE，连接PF、EF，则FC的最小值是 ，点F到线段BC的最短距离是 ．
【解答】解：连接CE，作EG⊥BC于G，
∵AE＝EF＝2，
∴点F在以E为圆心，AE为半径的圆上运动，
在Rt△CDE中，由勾股定理得，
CE＝＝＝2，
∴FC的最小值为CE﹣2＝2﹣2，
∵∠DAB＝∠ABC＝∠BGE＝90°，
∴四边形ABGE是矩形，
∴EG＝AB＝4，
∴点F到线段BC的最短距离是2，
故答案为：2﹣2，2．
【典例4】（2021秋•邗江区期末）如图，在平面直角坐标系xOy中，已知点A（1，0），B（3，0），C为平面内的动点，且满足∠ACB＝90°，D为直线y＝x上的动点，则线段CD长的最小值为（ ）
A．1B．2C．D．
【解答】解：∵∠ACB＝90°，
∴点C在以AB为直径的圆上，
AB为直径的圆的圆心为E点，如图，
连接DE交⊙E于C′，
∵A（1，0），B（3，0），
∴AB＝2，AE＝1，
∴DC≤DE﹣CE（当且仅当D、C、E共线时取等号）
即DC≤DE﹣1，
∵DE⊥直线y＝x时，DE最短，DE的最小值为OE＝，
∴线段CD长的最小值为﹣1．
故选：C．
【变式4-1】（2021秋•武江区校级期末）如图，⊙M的半径为4，圆心M的坐标为（5，12），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为 ．
【解答】解：连接OP，
∵PA⊥PB，
∴∠APB＝90°，
∵AO＝BO，
∴AB＝2PO，
若要使AB取得最小值，则PO需取得最小值，
连接OM，交⊙M于点P′，当点P位于P′位置时，OP′取得最小值，过点M作MQ⊥x轴于点Q，
则OQ＝5，MQ＝12，
∴OM＝13，
又∵MP′＝4，
∴OP′＝9，
∴AB＝2OP′＝18，
故答案是：18．
【变式4-2】（2021秋•萨尔图区校级期末）如图，点A，B的坐标分别为A（4，0），B（0，4），C为坐标平面内一点，BC＝2，点M为线段AC的中点，连接OM，OM的最大值为 ．
【解答】解：∵C为坐标平面内一点，BC＝2，
∴点C的运动轨迹是在半径为2的⊙B上，
如图，取OD＝OA＝4，连接OD，
∵点M为线段AC的中点，
∴OM是△ACD的中位线，
∴OM＝，
∴OM最大值时，CD取最大值，此时D、B、C三点共线，
此时在Rt△OBD中，BD＝＝4，
∴CD＝2+4，
∴OM的最大值是1+2．
故答案为：1+2．
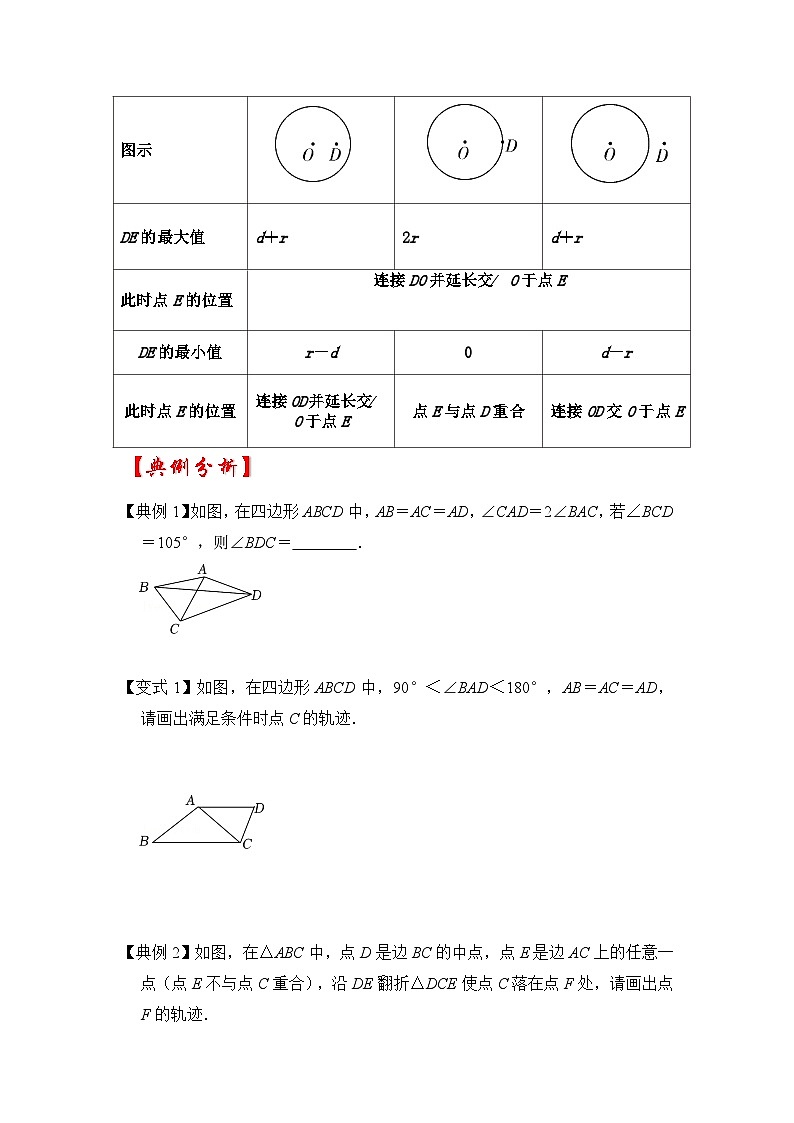
位置关系
点D在O内
点D在O上
点D在O外
图示
DE的最大值
d＋r
2r
d＋r
此时点E的位置
连接DO并延长交O于点E

DE的最小值
r－d
0
d－r
此时点E的位置
连接OD并延长交O于点E
点E与点D重合
连接OD交O于点E
位置关系
点D在O内
点D在O上
点D在O外
图示
DE的最大值
d＋r
2r
d＋r
此时点E的位置
连接DO并延长交O于点E

DE的最小值
r－d
0
d－r
此时点E的位置
连接OD并延长交O于点E
点E与点D重合
连接OD交O于点E