



- 专题05 易错题精选05之分式方程及应用专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题06 易错题集锦06之反比例函数专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题08 选择压轴题精选-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题09 压轴大题精选01之动点专练-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题10 压轴大题精选(综合)-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
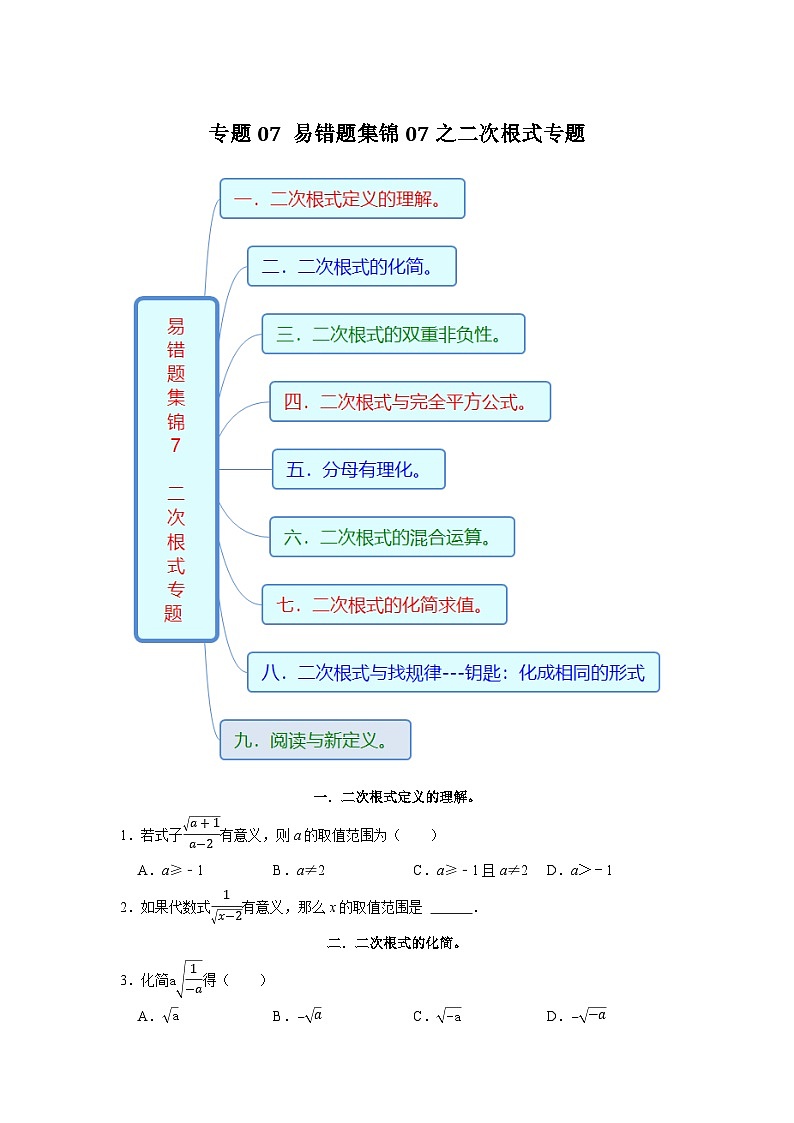
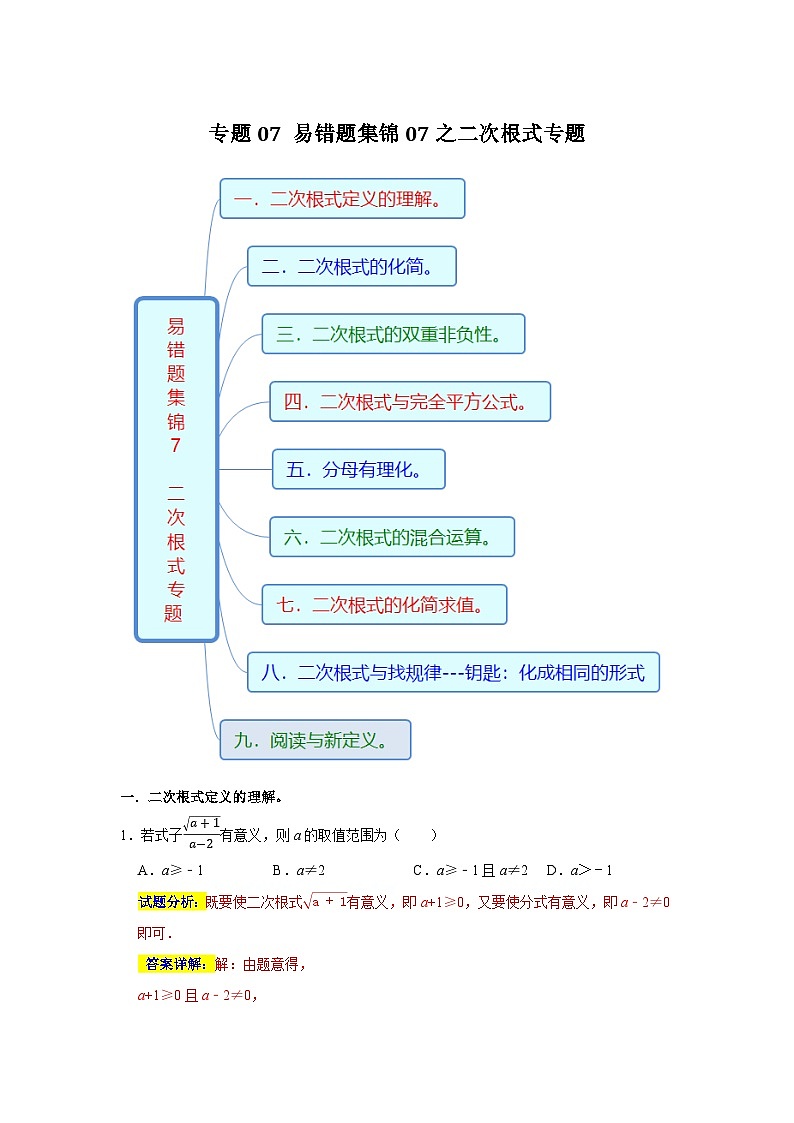
专题07 易错题集锦07之二次根式专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版)
展开一.二次根式定义的理解。
1.若式子a+1a−2有意义,则a的取值范围为( )
A.a≥﹣1B.a≠2C.a≥﹣1且a≠2D.a>﹣1
试题分析:既要使二次根式a+1有意义,即a+1≥0,又要使分式有意义,即a﹣2≠0即可.
答案详解:解:由题意得,
a+1≥0且a﹣2≠0,
即a≥﹣1且a≠2,
所以选:C.
2.如果代数式1x−2有意义,那么x的取值范围是 x>2 .
试题分析:根据二次根式和分式有意义的条件列不等式组求解.
答案详解:解:由题意可得:x﹣2>0,
解得:x>2.
所以答案是:x>2.
二.二次根式的化简。
3.化简a1−a得( )
A.aB.−aC.−aD.−−a
试题分析:根据二次根式的性质化简即可.
答案详解:解:原式=a•−a−a
=−−a.
所以选:D.
4.已知|a|=3,b2=5,且|a+b|=a+b,那么a+b的值是( )
A.2或8B.2或﹣8C.﹣2或8D.﹣2或﹣8
试题分析:根据二次根式的性质与化简,立方根的意义,进行计算逐一判断即可解答.
答案详解:解:∵|a|=3,b2=5,
∴a=±3,b=±5,
∵|a+b|=a+b,
∴a+b≥0,
∴当a=3,b=5时,a+b=3+5=8,
当a=﹣3,b=5时,a+b=﹣3+5=2,
综上所述:a+b的值是2或8,
所以选:A.
5.实数a,b在数轴上对应点的位置如图所示,化简|﹣a|+(a−b)2的结果是( )
A.﹣2a+bB.2a﹣bC.﹣bD.无意义
试题分析:利用绝对值的意义和二次根式的性质化简运算即可.
答案详解:解:由实数a,b在数轴上对应点的位置可得:a<0,b>0,|a|>|b|,
∴﹣a>0,a﹣b<0,
∴原式=﹣a+(b﹣a)
=﹣a+b﹣a
=﹣2a+b,
所以选:A.
6.已知12<a<1,化简:|a−(a−1)2|= 2a﹣1 .
试题分析:利用二次根式的性质和绝对值的意义化简运算即可.
答案详解:解:∵12<a<1,
∴a﹣1<0,2a﹣1>0.
原式=|a﹣(1﹣a)|
=|a﹣1+a|
=|2a﹣1|
=2a﹣1.
所以答案是:2a﹣1.
7.已知2<a<3,化简:a2−2a+1+(a−4)2= 3 .
试题分析:利用二次根式的性质化简求值即可.
答案详解:解:原式=(a−1)2+(a−4)2,
∵2<a<3,
∴原式=a﹣1+(4﹣a)=3.
所以答案是:3.
8.已知12x是整数,那么正整数x的最小值是 3 .
试题分析:把12分解质因数,然后根据二次根式的性质解答.
答案详解:解:∵12=4×3,
∴12x是整数的正整数x的最小值是3.
所以答案是:3.
9.已知n是正整数,18n是整数,则n的最小值为 2 .
试题分析:由n为正整数,18n也是正整数,知18n是一个完全平方数,再将18分解质因数,从而得出结果.
答案详解:解:n为正整数,18n也是正整数,
则18n是一个完全平方数,
又18n=2×32n=32•(2n),
则2n是一个完全平方数,
所以n的最小值是2.
所以答案是:2.
10.若二次根式3a+5是最简二次根式,则最小的正整数a= 2 .
试题分析:判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
答案详解:解:二次根式3a+5是最简二次根式,则最小的正整数a=2,
所以答案是:2.
三.二次根式的双重非负性。
11.已知y=2x−1−1−2x+8x,则4x+5y−6的算术平方根为 2 .
试题分析:根据被开方数大于等于0列式求出x的值,再求出y的值,然后代入代数式求出4x+5y−6的值,再根据算术平方根的定义解答.
答案详解:解:由题意得,2x﹣1≥0且1﹣2x≥0,
解得x≥12且x≤12,
∴x=12,
∴y=2x−1−1−2x+8x=0+0+8×12=4,
∴4x+5y−6=4×12+5×4−6=4,
∴4x+5y−6的算术平方根是2.
所以答案是:2.
12.若y=x−3+6−2x+2,则2x﹣y的算术平方根为 2 .
试题分析:直接利用二次根式的定义得出x的值,进而得出y的值,再根据算术平方根的定义解答即可.
答案详解:解:由题意得x−3≥06−2x≥0,
解得x=3,
所以y=2,
所以2x﹣y=6﹣2=4,
所以2x﹣y的算术平方根为2.
所以答案是:2.
13.已知y=1−2x+2x−1+2,则xy= 1 .
试题分析:直接利用二次根式的性质得出x的值以及y的值,进而得出答案.
答案详解:解:∵y=1−2x+2x−1+2,
∴1﹣2x=0,
∴x=12,
∴y=2,
∴xy=12×2=1.
∴xy=1.
所以答案是:1.
14.已知y=1+2x−1+1−2x,则2x+3y的平方根为 ±2 .
试题分析:先根据二次根式有意义的条件求出x的值,进而得出y的值,根据平方根的定义即可得出结论.
答案详解:解:∵2x−1≥01−2x≥0,
∴x=12,
∴y=1,
∴2x+3y=2×12+3×1=4,
∴2x+3y的平方根为±2.
所以答案是:±2.
四.二次根式与完全平方公式。
15.【阅读材料】小明在学习二次根式时,发现一些含根号的式子可以化成另一个式子的平方,
如:5+26=(2+3)+22×3=(2)2+(3)2+22×3=(2+3)28+27=(1+7)+21×7=12+(7)2+2×1×7=(1+7)2
【类比归纳】
(1)请你仿照小明的方法将7+210化成另一个式子的平方.
【变式探究】
(2)若a+221=(m+n)2且a,m,n均为正整数,求a值.
试题分析:(1)根据所给的方法进行求解即可;
(2)利用所给的方法进行分析,即可求解.
答案详解:解:(1)7+210
=(2+5)+22×5
=(2)2+(5)2+22×5
=(2+5)2;
(2)∵a+221=(m+n)2,
∴a+23×7=(m+n)2,
a+221×1=(m+n)2,
∴a=3+7=10或a=21+1=22.
16.【阅读材料】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+22=(1+2)2.善于思考的小明进行了以下探索:若设a+b2=(m+n2)2=m2+2n2+2mn2(其中a、b、m、n均为整数),则有a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b2的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
【问题解决】
(1)若a+b5=(m+n5)2,当a、b、m、n均为整数时,则a= m2+5n2 ,b= 2mn .(均用含m、n的式子表示)
(2)若x+43=(m+n3)2,且x、m、n均为正整数,分别求出x、m、n的值.
【拓展延伸】
(3)化简5+26= 2+3 .
试题分析:(1)根据完全平方公式将等式右边展开,然后分析求解;
(2)根据完全平方公式将等式右边展开,然后列方程求解;
(3)根据完全平方公式和二次根式的性质进行变形化简.
答案详解:解:(1)(m+n5)2=m2+25mn+5n2,
∵a+b5=(m+n5)2,且a、b、m、n均为整数,
∴a=m2+5n2,b=2mn,
所以答案是:m2+5n2,2mn;
(2)(m+n3)2=m2+23mn+3n2,
∵x+43=(m+n3)2,
∴2mn=4m2+3n2=x,
又∵x、m、n均为正整数,
∴m=1n=2x=13或m=2n=1x=7,
即m=1,n=2,x=13或m=2,n=1,x=7;
(3)原式=(2)2+26+(3)2
=(2+3)2
=2+3,
所以答案是:2+3.
五.分母有理化。
17.设x=45+3,y=5−3,则x,y的大小关系是( )
A.x>yB.x≥yC.x<yD.x=y
试题分析:把x的值分母有理化,再比较.
答案详解:解:∵x=4(5−3)−4=3−5>0,y=5−3<0.
∴x>y,
所以选:A.
18.阅读材料:我们已经知道,形如ca±b的无理数的化简要借助平方差公式:
例如:32−3=3×(2+3)(2−3)(2+3)=6+3322−(3)2=6+334−3=6+33.下面我们来看看完全平方公式在无理数化简中的作用.
问题提出:7+43该如何化简?
建立模型:形如m+2n的化简,只要我们找到两个数a,b,使a+b=m,ab=n,这样(a)2+(b)2=m,a⋅b=n,
那么便有:m±2n=(a±b)2=a±b(a>b),
问题解决:化简:7+43,
解:首先把7+43化为7+212,这里m=7,n=12,由于4+3=7,4×3=12,即(4)2+(3)2=7,4×3=12
∴7+43=7+212=(4+3)2=2+3.
模型应用1:利用上述解决问题的方法化简下列各式:
(1)6+25;
(2)13−410;
模型应用2:
(3)在Rt△ABC中,∠C=90°,AB=4−3,AC=3,那么BC边的长为多少?(结果化成最简).
试题分析:(1)先根据完全平方公式进行变形,再求出即可;
(2)先根据完全平方公式进行变形,再求出即可;
(3)根据勾股定理求出即可.
答案详解:解:(1)这里m=6,n=5,由于1+5=6,1×5=5,
即12+(5)2=6,1×5=5,
所以:6+25
=12+2×1×5+(5)2
=(1+5)2
=1+5;
(2)首先把13−410化为13−240,这里m=13,n=40,由于5+8=13,5×8=40,
即(5)2+(8)2=13,5×8=40,
所以13−410
=13−240
=(5)2−2×5×8+(8)2
=(5−8)2
=8−5
=22−5;
(3)在Rt△ABC中,由勾股定理得,AC2+BC2=AB2,
所以,(3)2+BC2=(4−3)2
所以,BC=16−83=23−2.
六.二次根式的混合运算。
19.(1)3−27+|2−3|−9+(12)2;
(2)40−5110−10.
试题分析:(1)先化简各式,然后再进行计算,即可解答;
(2)先把每一个二根式化成最简二次根式,然后再进行计算即可解答.
答案详解:解:(1)3−27+|2−3|−9+(12)2
=3−27+2−3−3+14
=−1114;
(2)40−5110−10
=210−102−10
=102.
20.(1)计算:8⋅6−343;
(2)计算:45+|2−5|−(π−3)0.
试题分析:(1)先算乘法,化为最简二次根式,再合并同类二次根式即可;
(2)先化为最简二次根式,去绝对值,算零指数幂,再合并即可.
答案详解:解:(1)原式=48−3×233
=43−23
=23;
(2)原式=35+5−2﹣1
=45−3.
21.计算:
(1)212−613+348
(2)213×318÷56
(3)(5−2)(5+2)+(3−1)2
试题分析:(1)根据二次根式的加减进行计算即可求解;
(2)根据二次根式的乘除进行计算即可求解;
(3)根据二次根式的混合运算进行计算即可求解.
答案详解:解:(1)原式=2×23−6×33+3×43
=43−23+123
=143;
(2)原式=613×18÷56
=66×65
=6×615
=3655;
(3)原式=5−2+(3−23+1)
=3+4−23
=7−23.
七.二次根式的化简求值。
22.先化简,再求值:x(6−x)+(x+5)(x−5),其中x=6−2.
试题分析:先计算整式的乘法,再合并同类项,然后把x=6−2代入化简后的结果,即可求解.
答案详解:解:原式=6x−x2+x2−5=6x−5,
当x=6−2时,
原式=6(6−2)−5=6−23−5=1−23.
23.先化简,再求值:(a−2)(a+2)+a(a−1a),其中a=−3.
试题分析:先用平方差公式和乘法法则化简,再代入即可.
答案详解:解:原式=a2﹣2+a2﹣1
=2a2﹣3,
把a=−3代入得:
原式=2×(−3)2﹣3
=2×3﹣3
=6﹣3
=3.
24.已知x=2−1,y=2+1,求x2−2xy+y2x2−y2的值.
试题分析:首先将分式因式分解进而将已知代入求出即可.
答案详解:解:∵x=2−1,y=2+1,
∴x2−2xy+y2x2−y2
=(x−y)2(x+y)(x−y)
=x−yx+y
=2−1−2−12−1+2+1
=−222
=−22.
八.二次根式与找规律---钥匙:化成相同的形式
25.观察下列等式:①12−1=2+1;②13−2=3+2;③14−3=4+3;…,请用字母n表示你所发现的律:即1n+1−n= n+1+n(n为正整数) .
试题分析:根据所给的等式即可求出规律.
答案详解:解:由所给的式子可知:原式=n+1+n(n为正整数)
所以答案是:n+1+n(n为正整数)
26.观察下列等式:
第1个等式:a1=11+2=2−1,
第2个等式:a2=12+3=3−2,
第3个等式:a3=13+2=2−3,
第4个等式:a4=12+5=5−2,
…
按上述规律,请写出第n个等式:an= 1n+n+1=n+1−n .
试题分析:根据所列举等式的所呈现的规律可得答案.
答案详解:解:根据规律可得,第n个等式:an=1n+n+1=n+1−n,
所以答案是:1n+n+1=n+1−n.
27.已知:对于正整数n,有1(n+1)n+nn+1=1n−1n+1,若某个正整数k满足
121+12+132+23+143+34+⋯+1(k+1)k+kk+1=23,则k= 8 .
试题分析:读懂规律,按所得规律把左边所有的加数写成1n−1n+1的形式,把互为相反数的项结合,可使运算简便.
答案详解:解:∵121+12+132+23+143+34+⋯+1(k+1)k+kk+1=23,
∴11−12+12−13+13−14+⋯+1k−1k+1=23,
即1−1k+1=23,
∴1k+1=13,
解得k=8.
所以答案是:8.
28.阅读下列解题过程:
12+1=2−1(2+1)(2−1)=2−1
13+2=3−2(3+2)(3−2)=3−2
14+3=4−3(4+3)(4−3)=4−3;
…
则:
(1)110+9= 10−3 ;1100+99= 10﹣311 ;
(2)观察上面的解题过程,请直接写出式子1n−n−1= n+n−1 ;
(3)利用这一规律计算:(12+1+13+2+14+3+⋯+12009+2008)(2009+1)的值.
试题分析:(1)先分母有理化,再求出即可.
(2)根据已知的算式的结果得出即可.
(3)先根据已知得出(2−1+3−2+4−3+⋯+2009−2008)(2009+1),合并后根据平方差公式求出即可.
答案详解:解:(1)110+9=10−9(10+9)(10−9)=10−9=10−3,
1100+99=100−99(100+99)(100−99)=100−99=10﹣311
所以答案是:10−3,10﹣311.
(2)1n−n−1=n+n−1,
所以答案是:n+n−1.
(3)原式=(2−1+3−2+4−3+⋯+2009−2008)(2009+1)
=(2009−1)(2009+1)
=2009﹣1
=2008.
九.阅读与新定义。
29.我们规定用(a,b)表示一对数对,给出如下定义:记m=1a,n=b(a>0,b>0),将(m,n)与(n,m)称为数对(a,b)的一对“对称数对”.
例如:(4,1)的一对“对称数对”为(12,1)与(1,12).
(1)求数对(25,4)的一对“对称数对”;
(2)若数对(3,y)的一对“对称数对”的两个数对相同,求y的值;
(3)若数对(a,b)的一对“对称数对”的一个数对是(3,33),求ab的值.
试题分析:(1)根据“对称数对”的定义求解.
(2)根据“对称数对”定义建立关于y的方程求解.
(3)根据“对称数对”的定义建立关于a,b的方程求解.
答案详解:解:(1)由题意得:m=125=15,n=4=2,
∴(25,4)的一对“对称数对”为(15,2)与(2,15).
(2)由题意,m=13=33,n=y,
∵数对(3,y)的一对“对称数对”的两个数对相同,
∴m=n,
∴33=y,
∴y=13.
(3)由题意得:1a=3,b=33或1a=33,b=3,
∴a=13,b=27或a=127,b=3.
∴ab=9或ab=19.
30.请阅读下面材料,并解决问题:
海伦——秦九韶公式
海伦(约公元50年),古希腊几何学家,在数学史上以解决几何测量问题闻名,在他的著作《度量》一书中证明了一个利用三角形的三条边长直接求三角形面积的公式:
假设在平面内,有一个三角形的三条边长分别为a,b,c,记p=a+b+c2,那么三角形的面积
S=p(p−a)(p−b)(p−c).这个公式称为海伦公式.
秦九韶(约1202﹣1261年),我国南宋时期的数学家,曾提出利用三角形的三边长求面积的秦九韶公式S=14[a2b2−(a2+b2−c22)2].它填补了中国数学史中的一个空白,从中可以看出中国古代已经具有很高的数学水平.通过公式变形,可以发现海伦公式和秦九韶公式实质是同一个公式,所以海伦公式也称海伦﹣秦九韶公式.
问题:如图,在△ABC中,AB=6,AC=7,BC=8,请用海伦一秦九韶公式求△ABC的面积.
试题分析:代入公式,进行二次根式的化简.
答案详解:解:∵AB=6,AC=7,BC=8,
∴a=8,b=7,c=6,
∴S=14×[64×49−(64+49−362)2]=21154.
31.阅读下列材料,并回答问题:
把形如a+bm与a﹣bm(a、b为有理数且b>0,m为正整数且开方开不尽)的两个实数称为共轭实数.
(1)请你举出一对共轭实数: 3+2 和 3−2 ;
(2)﹣25和25是共轭实数吗?若是,请指出a、b的值;
(3)若两个共轭实数的和是10,差的绝对值是43,请求出这两个共轭实数.
试题分析:(1)根据题意,可以写出一组共轭实数,本题答案不唯一;
(2)根据共轭实数的定义,可以判断﹣25和25是共轭实数,并写出a和b即可;
(3)根据两个共轭实数的和是10,差的绝对值是43,可以求得a、b、m的值,从而可以写出这两个共轭实数.
答案详解:解:(1)由题意可得,
3+2与3−2是共轭实数,
所以答案是:3+2,3−2;
(2)﹣25和25是共轭实数,a=0,b=2;
(3)设这两个共轭实数为a+bm与a﹣bm,
∵两个共轭实数的和是10,差的绝对值是43,
∴(a+bm)+(a﹣bm)=10,|(a+bm)﹣(a﹣bm)|=43,
∴2a=10,|2bm|=43,
∴a=5,b=2或b=﹣2(舍去),m=3,
∴这两个共轭实数是5+23,5﹣23.
专题06 易错题集锦06之反比例函数专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题06 易错题集锦06之反比例函数专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题06易错题集锦06之反比例函数专题原卷版docx、专题06易错题集锦06之反比例函数专题解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
专题05 易错题精选05之分式方程及应用专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题05 易错题精选05之分式方程及应用专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题05易错题精选05之分式方程及应用专题原卷版docx、专题05易错题精选05之分式方程及应用专题解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
专题04 易错题精选04之最值专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题04 易错题精选04之最值专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题04易错题精选04之最值专题原卷版docx、专题04易错题精选04之最值专题解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。












