2024年中考数学压轴题专项练习—轴对称（最短路线问题）

这是一份2024年中考数学压轴题专项练习—轴对称（最短路线问题），文件包含86轴对称最短路线问题答案docx、86轴对称最短路线问题docx等2份试卷配套教学资源，其中试卷共46页， 欢迎下载使用。
1、以专题复习为主。如选择题、填空题的专项练习，要把握准确度和时间的安排。加强对二次函数与几何图形结合的综合性试题、实际应用题等专题的练习，深化对常考题型的熟悉程度。在函数复习过程中，如果考生未能完全理解简单实例中的数量关系和变化规律，针对此类问题，在专项复习中，可以通过选择题、填空题的专项练习，进行突破，如“读懂图象信息问题”等，将复杂问题由浅入深，层层分解，提高分析和判断能力。
2、重视方法思维的训练。对初中数学所涉及的函数思想、方程思想、数形结合思想、分类讨论思想、转化与化归思想、整体思想等数学思想方法，要通过典型试题的训练，进一步渗透和深刻理解其内涵，重要处舍得投入时间与精力。强化解题过程中常用的配方法、待定系数法等通法。
3、拓宽思维的广度，培养多角度、多维度思考问题的习惯。将专项复习中的共性习题串连起来，通过一题多解，积极地探求解决问题的最优解法，这样，对于解决难度较大的压轴题会有很大的帮助。
轴对称—最短路线问题
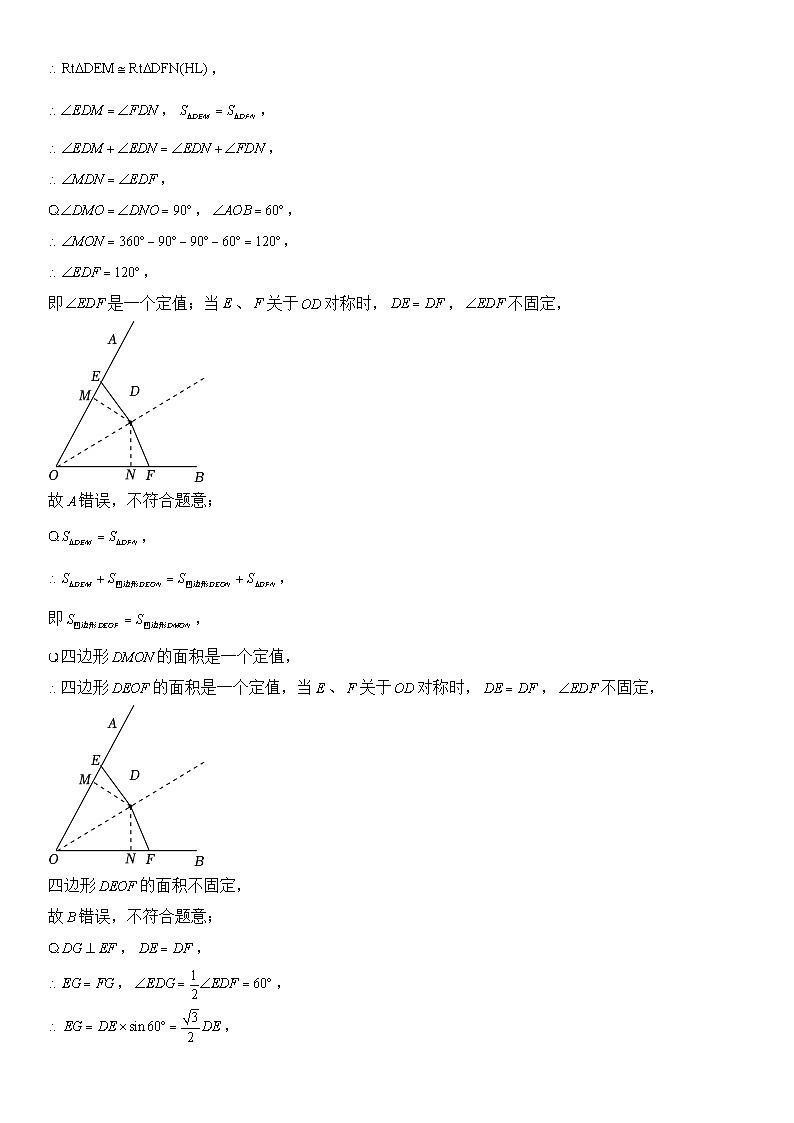
1．（2023•南皮县校级三模）如图，已知，点是的平分线上的一点，点，分别是射线和射线上的点，且，．下列结论中正确的是
A．是一个定值
B．四边形的面积是一个定值
C．当时，的周长最小
D．当时，也平行
2．（2022秋•青山区期末）如图，在中，，，为边上一动点，连接．以为底边，在的左侧作等腰直角三角形，点是边上的定点，连接，当取最小值时，若，则为 （用含的式子表示）
A．B．C．D．
3．（2022•鄂州）如图，定直线，点、分别为、上的动点，且，在两直线间运动过程中始终有．点是上方一定点，点是下方一定点，且，，，，当线段在平移过程中，的最小值为
A．B．C．D．
4．（2022•景县校级模拟）如图，，点到的距离是2，到的距离是3，，分别是，上的动点，则周长的最小值是
A．B．C．9D．
5．（2021秋•淇滨区月考）如图．已知．，为的平分线，且，点、分别是边和上的动点，则周长的最小值为
A．4B．6C．D．10
6．（2020•荆门）在平面直角坐标系中，长为2的线段（点在点右侧）在轴上移动，，，连接，，则的最小值为
A．B．C．D．
7．（2020•安徽模拟）中，，，，，是和上的动点，连接，，则的最小值为
A．8B．C．D．
8．（2018春•江岸区校级月考）中，，、两点在边上，，，，若点、分别在边、上，当四边形的周长最小时，的值为
A．B．C．D．
9．（2018春•沙坪坝区校级期末）如图，，点、分别在射线、上，且，，点、分别是射线、上的动点，当最小时，的值为
A．20B．26C．32D．36
10．如图，在矩形中，对角线，过点作，垂足为，，点，分别在，上，则的最小值为
A．B．C．D．
11．（2023•陵城区校级一模）如图，在菱形中，，，，分别是边和对角线上的动点，且，则的最小值为 ．
12．（2022•温江区校级自主招生）如图，在矩形中，连接对角线，在线段上存在一动点，取线段中点，连接，并以为对称轴作点的对称点，再以为对称轴作点的对称点，连接，，在内有一动点，分别连接，，，已知，，则在运动的过程中，的最小值为 ．
13．（2022春•即墨区期末）在中，，是的角平分线，在的垂直平分线上，，为上的动点，则的最小值为 ．
14．（2021秋•柯桥区期末）如图，，平分，平分，和交于点，，分别是线段和线段上的动点，且，若，，则的最小值为 ．
15．（2022•海安市模拟）如图，在正方形中，点，在，上运动，且，在上截取一点，满足，连接，取，的中点，，连接，，令，交于，两点，若，当的取值最小时，则的长度为 ．
16．（2021•邛崃市模拟）如图，在中，，，，点在内，连接、、，则的最小值是 ．
17．（2021•潼关县二模）如图，在矩形中，，，为上一点，连接，将线段绕点顺时针得到线段，连接、，则的最小值为 ．
18．（2021•通州区二模）如图，在边长为2的正方形中，点在边上，点在对角线上，连接，．若，则的最小值为 ．
19．（2023春•西峡县期末）如图，在四边形中，，，在边，上分别找一点，使的周长最小，此时 ．
20．（2023•青岛一模）如图，在正方形中，的平分线交边于点，点在边上，，连接分别交和于点、，动点在上，于点，连接，则下列结论正确的是：①；②；③；④若，则的最小值是．其中正确的是 （填写序号）
21．（2023春•广陵区期末）如图，在正方形中，，与相交于点，是的中点，，为对角线上的两点，若，则的最小值为 ．
22．（2023春•涪城区期中）如图，在平行四边形中，，．连接，且，平分交与于点．点在边上，，若，线段（点在点的左侧）在线段上运动，，连接．，则的最小值为 ．
23．（2023•淮安二模）如图，在边长为8的正方形中，点为正方形的中心，点为边上的动点，连接，作交于点，连接，为的中点，为边上一点，且，连接，，则的最小值为 ．
24．（2023春•淮北月考）如图，正方形的边长为4，，分别是边、上的动点，且，连接，交于点，是边上的另一个动点，连接，，则的最小值为 ．
25．（2023•龙子湖区二模）如图，在正方形中，，是上的一点，且，，是，上的动点，且，，连接，，当的值最小时，的长为 ．
26．（2023•临潼区三模）如图所示，为矩形中边上的一点，已知，，若点在矩形内部，且，则的最小值为 ．
27．（2023•凤阳县二模）如图，直线，在直线上方作等边，点，在直线上，延长交直线于点，在上方作等边，点在直线上且在点右边．动点，分别在直线，上，且，若，则的最小值是 ．
28．（2023•济宁一模）如图，在菱形中，，，点是上一点，点、分别是、上任意一点，且，垂足为，连接、，则的最小值为 ．
29．（2022秋•沙坪坝区校级期末）如图，在平面直角坐标系中，点，是第二象限角平分线上的两点，点的纵坐标为2，且，在轴上取一点，连接，，，，使得四边形的周长最小，则周长的最小值为 ．
30．（2022秋•邹城市校级期末）如图，点在射线上，以为边作等边，为中点，且，为中点，当最小时， ．