山东省青岛市崂山区金家岭学校2023年中考数学模拟试卷(含答案)

这是一份山东省青岛市崂山区金家岭学校2023年中考数学模拟试卷(含答案)，共19页。试卷主要包含了计算的结果为，化简等内容，欢迎下载使用。
1．如图，数轴上有A，B，C，D四个点，其中表示互为相反数的点是（ ）
A．点B与点DB．点A与点CC．点A与点DD．点B与点C
【解答】解：2与﹣2互为相反数，
故选：C．
2．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
【解答】解：A．是轴对称图形，不是中心对称的图形，故本选项不符合题意；
B．不是轴对称图形，是中心对称的图形，故本选项不符合题；
C．是轴对称图形，不是中心对称的图形，故本选项不符合题意；
D．既是轴对称图形，又是中心对称的图形，故本选项符合题意．
故选：D．
3．2021年2月25日，习总书记在全国脱贫攻坚总结表彰大会上庄严宣告，我国脱贫攻坚战取得全面胜利，现行标准下9899万农村贫困人口全面脱贫．数据“9899万”用科学记数法可表示为（ ）
A．98.99×106B．9.899×107C．989.9×105D．0.9899×108
【解答】解：9899万＝98990000＝9.899×107．
故选：B．
4．计算的结果为（ ）
A．B．C．D．
【解答】解：=
故选：D
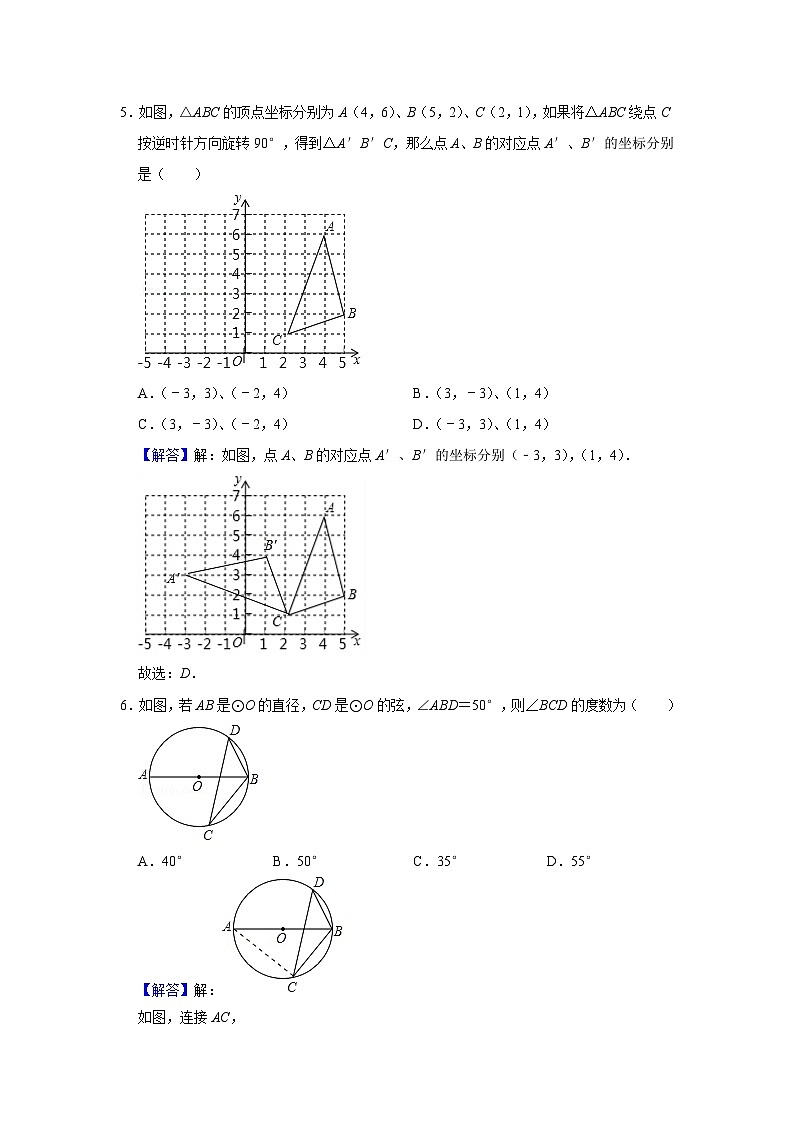
5．如图，△ABC的顶点坐标分别为A（4，6）、B（5，2）、C（2，1），如果将△ABC绕点C按逆时针方向旋转90°，得到△A′B′C，那么点A、B的对应点A′、B′的坐标分别是（ ）
A．（﹣3，3）、（﹣2，4）B．（3，﹣3）、（1，4）
C．（3，﹣3）、（﹣2，4）D．（﹣3，3）、（1，4）
【解答】解：如图，点A、B的对应点A′、B′的坐标分别（﹣3，3），（1，4）．
故选：D．
6．如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD＝50°，则∠BCD的度数为（ ）
A．40°B．50°C．35°D．55°
【解答】解：
如图，连接AC，
∵AB为直径，
∴∠ACB＝90°，
∵∠ABD＝50°，
∴∠ACD＝∠ABD＝50°，
∴∠BCD＝∠ACB﹣∠ACD＝90°﹣50°＝40°，
故选：A．
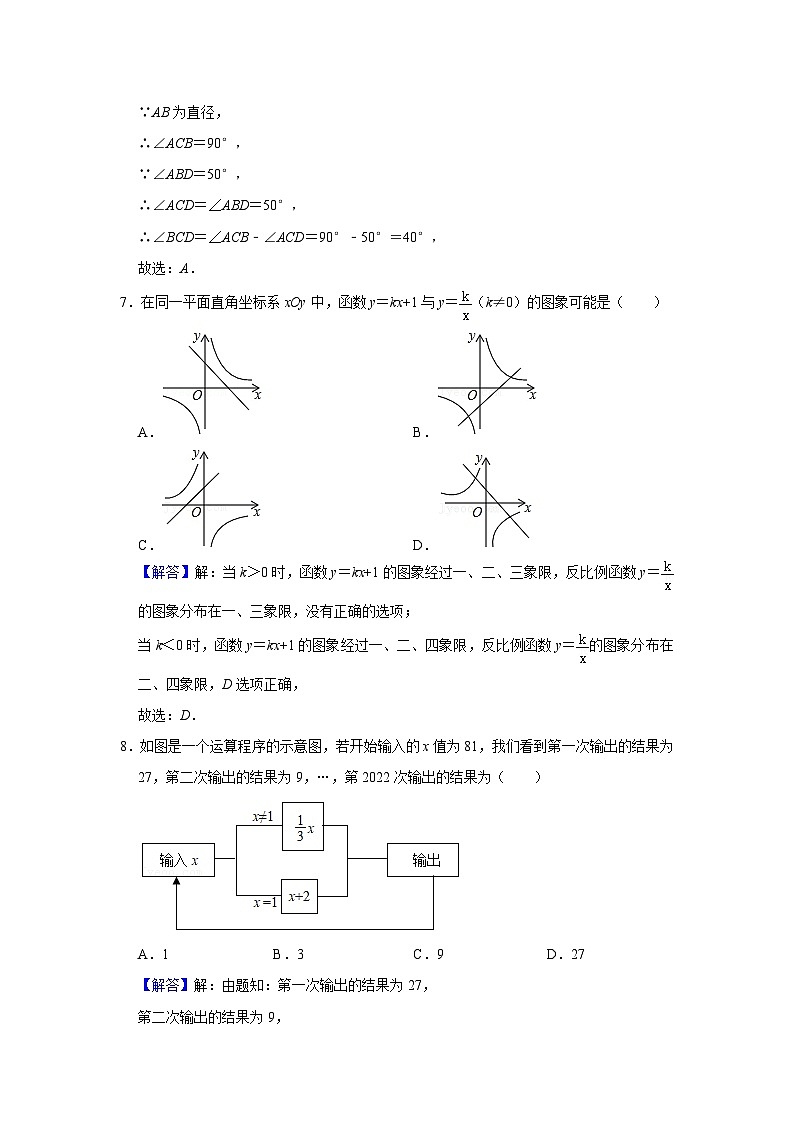
7．在同一平面直角坐标系xOy中，函数y＝kx+1与y＝（k≠0）的图象可能是（ ）
A．B．
C．D．
【解答】解：当k＞0时，函数y＝kx+1的图象经过一、二、三象限，反比例函数y＝的图象分布在一、三象限，没有正确的选项；
当k＜0时，函数y＝kx+1的图象经过一、二、四象限，反比例函数y＝的图象分布在二、四象限，D选项正确，
故选：D．
8．如图是一个运算程序的示意图，若开始输入的x值为81，我们看到第一次输出的结果为27，第二次输出的结果为9，…，第2022次输出的结果为（ ）
A．1B．3C．9D．27
【解答】解：由题知：第一次输出的结果为27，
第二次输出的结果为9，
第三次输出的结果为3，
第四次输出的结果为1，
第五次输出的结果为3，
第六次输出的结果为1，
．
从第三次开始奇数次输出为3，偶数次输出为1，
∴第2022次输出结果为1，
故选：A．
二．填空题（共5小题）
9．化简：
【解答】解：
10．某内陆国家为了落实国家“一带一路”战略，促进经济发展，增强对外贸易的竞争力，把距离港口420km的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了2h．求汽车原来的平均速度．设汽车原来的平均速度为xkm/h，则可列方程为 ＝+2 ．
【解答】解：设汽车原来的平均速度为xkm/h，则公路升级后汽车的平均速度为（1+50%）xkm/h，
依题意，得：＝+2．
故答案为：＝+2．
11．一元二次方程的根完全由它的系数确定，并且可以由判别式来判断根的情况，已知关于的一元二次方程（a﹣3）x2﹣4x+4＝0有实数根，则a的取值范围为 ．
a≥2且a≠3 ．
【解答】解：由题意可知：Δ＝16+16（a﹣3）≥0且a﹣3≠0，
∴a≥2且a≠3，
故a的取值范围为a≥2且a≠3，
故答案为：a≥2且a≠3．
12．化简：a+1+a（a+1）+a（a+1）2+…+a（a+1）2022＝ （a+1）2023 ．
【解答】解：原式＝（a+1）2+a（a+1）2+…+a（a+1）2022
＝（a+1）3+…+a（a+1）2022
＝（a+1）2023
故答案为：（a+1）2023
13．如图，扇形AOB中，半径OA＝2，圆心角∠AOB＝60°，以OA为直径的半圆交OB于点C，则图中两个阴影部分面积的差的绝对值是 ．
【解答】解：由OA＝2可得半圆的半径为1，
则半圆面积为π×12＝，
扇形AOB面积为＝，
则图中两个阴影部分面积的差的绝对值为＝，
故答案为：．
14．如图，在直角三角形纸片ABC中，∠ACB＝90°，AC＝2，BC＝4，点D在边AB上，以CD为折痕将△CBD折叠得到△CPD，CP与边AB交于点E，若△DEP为直角三角形，则BD的长是 或2﹣2
【解答】解：如图1中，当∠EDF＝90°时，作CH⊥AB于H．
在Rt△ACB中，∵AC＝2，BC＝4，
∴AB＝＝2，
∴CH＝＝，
∵∠ACB＝∠AHC＝90°，
∴∠ACH+∠BCH＝90°，∠BCH+∠B＝90°，
∴∠ACH＝∠B＝∠F，
∵CH∥DF，
∴∠F＝∠HCE，
∴∠ACH＝∠HCE，∠DCE＝∠DCB，
∴∠HCD＝45°，
∴HC＝HD＝，
∵AH＝＝，
∴BD＝AB﹣AH﹣DH＝2﹣＝．
如图2中，当∠DEF＝90°时，设DE＝x，则EF＝2x，DF＝BD＝x，
∵AE+DE+BD＝2，
∴+x+x＝2，
∴x＝2﹣，
∴BD＝x＝2﹣2．
综上所述，BD的长为或2﹣2．
故答案为或2﹣2．
三．解答题（共9小题）
15．已知：如图，四边形ABCD．
求作：点P，使PC∥AB，且点P到点A和点B的距离相等．
结论：
【解答】解：过C点作AB的平行线，再作AB的垂直平分线，它们相交于点P，
则点P为所作．
16．（1）计算：


（2）先化简在再求值：.其中
【解答】解：(1)原式=3
（2）原式=，代入，结果得
17．如图所示，这是一种手机平板支架的侧面结构简易示意图．已知托板长AB＝120mm，支撑板长CD＝80mm，底座长DE＝90mm．托板AB固定在支撑板顶端点C处，且CB＝40mm，托板AB可绕点C转动，支撑板CD可绕点D转动，若∠DCB＝90°，∠CDE＝60°，求点A到底座DE的距离．
【解答】解：过A作AM⊥DE，交ED的延长线于M，过C作CF⊥AM于F，过C作CN⊥DE，
由题意知，AC＝80mm，CD＝80mm，∠DCB＝90°，∠CDE＝60°，
在Rt△CDN中，CN＝CD•sin∠CDE＝80×＝40（mm），∠DCN＝90°﹣60°＝30°，
∵∠DCB＝90°，
∴∠BCN＝90°﹣30°＝60°，
∵AM⊥DE，CN⊥DE，
∴AM∥CN，
∴∠A＝∠BCN＝60°，
∴∠ACF＝90°﹣60°＝30°，
在Rt△AFC中，AF＝AC•sin∠ACF＝80×＝40（mm），
由图知四边形MNCF为矩形，
∴FM＝CN＝40（mm），
∴AM＝AF+FM＝（40+40）（mm），
∴点A到底座DE的距离为（40+40）mm．
18．某电视台举行文艺比赛，并通过网络对比赛进行直播．比赛现场有5名专家评委给每位参赛选手评分，场外观众可以通过网络给每位参赛选手评分．每位选手的最终得分由专家评分和观众评分确定．某选手参与比赛后，现场专家评分情况如下表：
场外有数万名观众参与评分，记观众所评的分数为x．将评分x按照7≤x＜8，8≤x＜9，9≤x≤10分组，分组，绘成频率分布直方图如图：
（1）现场专家评委对该选手评分的中位数为 9.7 ；众数为 10 ；
（2）求a的值，并用频率估计概率，估计某场外观众评分不小于9的概率；
（3）考虑以下两种方案来确定该选手的最终得分：
方案一：用所有专家与观众的评分的平均数作为该选手的最终得分；
方案二：分别计算专家评分的平均数和观众评分的平均数，用作为该选手最终得分．
①直接写出与的大小关系；
②请直接写出与的大小关系．
【解答】解：（1）由现场专家评分情况如下表可知，现场专家评委对该选手评分的中位数为9.7；众数为10，
故答案为：9.7，10；
（2）0.2×1+a×1+0.5×1＝1，解得a＝0.3；
设事件A表示“某场外观众评分不小于9”，则P（A）＝0.5；
（3）①＝（10+10+8.8+8.9+9.7）＝9.48，
＝7.5×0.2+8.5×0.3+9.5×0.5＝8.8，
故＞；
②∵＞，而观众人数远远大于专家人数，
∴把专家与观众合在一起的平均数，就越接近于，此时专家评分的权重很小，
而是专家评分的平均数与观众评分的平均数，再求出平均数，此时专家评分的平均数所占的权重为50%，相应的平均分就比原来有较大的提高，
∴＜．
19．如图，在平面直角坐标系xOy中，一次函数y1＝ax+b（a，b为常数，且a≠0）与反比例函数y2＝（m为常数，且m≠0）的图象交于点A（﹣4，2），B（2，n）．
（1）求反比例函数和一次函数的解析式．
（2）连接OA，OB，求△AOB的面积．
（3）直接写出当0＜y1＜y2时，自变量x的取值范围．
【解答】解：（1）∵A（﹣4，2），
∴将A坐标代入反比例函数解析式y2＝中，得m＝﹣8，
∴反比例函数解析式为y＝；
将B坐标代入y＝，得n＝﹣4，
∴B坐标（2，﹣4），
将A与B坐标代入一次函数解析式中，得，解得，
∴一次函数解析式为y1＝﹣x﹣2；
（2）当﹣x﹣2＝0时，解得x＝﹣2，
∵点A（﹣4，2）、点B（2，﹣4），
∴△AOB的面积为：＝6．
（3）直线y1＝﹣x﹣2与x轴的交点坐标为（﹣2，0），
故当0＜y1＜y2时，自变量x的取值范围为﹣4＜x＜﹣2．
20．如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交DE的延长线于F点，连接AD、CF，过点D作DG⊥CF于点G．
（1）求证：四边形ADCF是平行四边形；
（2）若AB＝3，BC＝5，若四边形ADCF是菱形，求DG的值
【解答】（1）证明：∵点D、E分别是边BC、AC的中点，
∴DE是△ABC的中位线，BD＝CD，
∴DE∥AB，
∵AF∥BC，
∴四边形ABDF是平行四边形，
∴AF＝BD，
∴AF＝DC，
∵AF∥BC，
∴四边形ADCF是平行四边形；
（2）∵四边形ADCF是菱形，
∴AC⊥DF，AD＝CD＝BD＝CF，
∴CF＝AD＝BC＝，
∴△ABC是直角三角形，∠BAC＝90°，
∴AC＝＝＝4，
由（1）可知，四边形ABDF是平行四边形，
∴DF＝AB＝3，
∵DG⊥CF，
∴S菱形ADCF＝AC•DF＝CF•DG，
即×4×3＝•DG，
∴DG＝，
故答案为：．
21．如图，AC是⊙O直径，D是的中点，连接CD交AB于点E，点F在AB延长线上且FC＝FE．
（1）求证：CF是⊙O的切线；
（2）若BF＝2，csF＝，求⊙O的半径．
【解答】（1）证明：连接BC，
∵AC是⊙O的直径，
∴∠ABC＝90°，
∴∠A+∠ACB＝90°，
∵FC＝FE，
∴∠FCE＝∠FEC，
∴∠FCB+∠DCB＝∠A+∠ACD，
∵D是的中点，
∴＝，
∴∠ACD＝∠DCB，
∴∠FCB＝∠A，
∴∠FCB+∠ACB＝90°，
∴∠OCF＝90°，
∵OC是⊙O的半径，
∴CF是⊙O的切线；
（2）解：在Rt△FBC中，BF＝2，csF＝＝，
∴CF＝3，
∴BC＝＝5，
∵∠CBF＝∠ACF＝90°，∠F＝∠F，
∴△FBC∽△FCA，
∴＝，
∴＝，
∴CA＝，
∴⊙O的半径为．
22．某农副产品经销商以30元/千克的价格收购农户们的一批农副产品进行销售，经过市场调查发现一部分数据如下：
其中，月销售量是关于销售价格的一次函数．
（1）请直接写出p与x之间的一次函数关系；
（2）该农副产品经销商应如何确定这批农副产品的销售价格，才能使得月销售利润最大？
（3）在（2）的条件下，该农副产品经销商打算把这一批农副产品运往A，B两个销售网点进行销售．根据市场要求，A销售网点的销量应不低于B销售网点的一半且不高于总销量的一半，运使往A、B两个销售网点的运费分别为a元/千克（其中a＞0），3元/千克，请直接写出最优的调运方案．
【解答】解：（1）∵p与x成一次函数关系，设函数关系式为p＝kx+b，
可选择x＝40，y＝6000和x＝50，y＝4800代入，
则：，
解得：，
∴所求的函数关系为p＝﹣120x+10800；
（2）设月销售利润为w元，
∴w＝p（x﹣30）＝（﹣120x+10800）（x﹣30），
即w＝﹣120x2+14400x﹣324000，
∴当x＝﹣＝60时，w有最大值，wmax＝﹣120×（60）2+14400×60﹣324000＝108000（元）
答：这批农产品的销售价格定为60元/千克时月销售利润有最大，这个最大月销售利润为108000元；
（3）根据（2）得月销量为：p＝﹣120×60+10800＝3600（kg），
设运往A网点mkg，则运往B网点（3600﹣m）kg，
由题意得：（3600﹣m）≤m≤×3600，
解得：1200≤m≤1800，
总运费M＝am+3（3600﹣m）＝10800+（a﹣3）m，
①当a＞3时，m取最小值1200时M最小，
此时，运往A地1200kg，运往B地3600﹣1200＝2400kg，
②当0＜a＜3时，m取最大值1800时M最小，
此时运往A地1800kg，运往B地3600﹣1800＝1800kg，
③a＝3时，在1200≤m≤1800范围内的所有方案都可以．
综上所述，最优方案：①a＞3时，运往A地1200kg，运往B地2400kg，
②a＜3时，运往A地1800kg，运往B地1800kg．③a＝3时，在1200≤m≤1800范围内的所有方案都可以．
23．先阅读下列材料，然后解答问题：
材料：从4张不同的卡片中选取2张，有6种不同的选法，抽象成数学问题就是从4个不同元素中选取2个元素的组合，组合数记为＝＝6．一般地，从n个不同元素中选取m个元素的组合数记作，＝（m≤n）．
例如：从6个不同元素中选3个元素的组合，组合数记作＝＝20
（1）为迎接国家建设工作检查，学校将举办小型书画展览．王老师在班级8幅优秀书画中选取3幅，共有多少种选法？
（2）探索发现：
计算：＝ 3 ，＝ 1 ，＝ 4 ，＝ 10 ，＝ 5 ，＝ 15 ．
由上述计算，试猜想，，之间有什么关系．（只写结论，不需说明理由）
（3）请你直接利用（2）中猜想的结论计算：++++…+．
【解答】解：（1）＝＝56
答：共有56种选法．
（2）＝3，＝1，＝4，＝10，＝5，＝15，
因为+＝，+＝，
所以Ckn+∁nk+1＝Cn+1k+1．
（3）++++…+
＝+++…+
＝+…+
＝
＝
＝165．
24．如图，四边形ABCD为矩形，AB＝4cm，AD＝3cm，动点M，N分别从点D，B同时出发，都以1cm/s的速度运动．点M沿DA向终点A运动，点N沿BC向终点C运动．过点N作NP⊥BC，交AC于点O，连接MP．已知动点运动了ts（0＜t＜3）．
（1）当t为多少时，PM∥AB？
（2）若四边形CDMP的面积为S，试求S与t的函数关系式．
（3）在运动过程中，是否存在某一时刻t使四边形CDMP面积与四边形ABCD面积比为3：8？若存在，请求出t的值；若不存在，请说明理由．
（4）在点M，N运动过程中，△MPA能否成为一个等腰三角形？若能，求出所有可能的t值；若不能，试说明理由．
【解答】解：（1）∵PM∥AB，AB∥PN，
∴PM与PN共直线，
∴MN∥AB，
∴AM＝NB，
∴3﹣t＝t，
得t＝；
（2）如图，延长NP交AD于点Q，则PQ⊥AD，
由题意知，DM＝BN＝t，AM＝CN＝3﹣t，
∵PN∥AB，
∴△PNC∽△ABC，
∴＝，即＝，
解得：PN＝（3﹣t）＝4﹣t，
∵PQ⊥AD，
∴∠QAB＝∠B＝∠NQA＝90°，
∴四边形ABNQ是矩形，
则AB＝QN＝4，
∴PQ＝QN﹣PN＝4﹣（4﹣t）＝t，
∴四边形CDMP的面积s＝×3×4﹣×（3﹣t）×t＝t2﹣2t+6；
（3）∵S矩形ABCD＝3×4＝12，
∴＝＝，
解得：t＝，
所以t＝时四边形CDMP的面积与四边形ABCD的面积比为3：8；
（4）△MPA能成为等腰三角形，共有三种情况，以下分类说明：
①若PM＝PA，
∵PQ⊥MA，
∴四边形ABNQ是矩形，
∴QA＝NB＝t，
∴MQ＝QA＝t，
又∵DM+MQ+QA＝AD
∴3t＝3，即t＝1
②若MP＝MA，则MQ＝3﹣2t，PQ＝t，MP＝MA＝3﹣t，
在Rt△PMQ中，由勾股定理得：MP2＝MQ2+PQ2
∴（3﹣t）2＝（3﹣2t）2+（t）2，
解得：t＝（t＝0不合题意，舍去）
③若AP＝AM，
由题意可得：AP＝t，AM＝3﹣t
∴t＝3﹣t，
解得：t＝
综上所述，当t＝1或t＝或t＝时，△MPA是等腰三角形．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：
专家
A
B
C
D
E
评分
10
10
8.8
8.9
9.7
销售价格x（元/千克）
40
50
60
月销售量p（千克）
6000
4800
3600