吉林省长春市绿园区2022-2023学年七年级下学期开学考试数学试卷(含答案)

这是一份吉林省长春市绿园区2022-2023学年七年级下学期开学考试数学试卷(含答案)，共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．的相反数是( )
A.B.C.D.
2．2022年10月12日，“神舟十四号”飞行乘组，在距地面约390000米的中国空间站问天实验舱开展第三次天宫授课，大大激发了广大青少年的追求科学的兴趣，数据“390000”用科学记数法表示为( )
A.B.C.D.
3．单项式的系数是( )
A.B.2C.3D.8
4．用式子表示“比a的平方的2倍小1的数”为( )
A.B.C.D.
5．如图是一个由6个相同的正方体组成的立体图形，它的主视图是( )
A.B.C.D.
6．把弯曲的河道改直，能够缩短航程，理由是( )
A.两点之间，线段最短B.经过一点有无数条直线
C.两点之间，直线最短D.两点确定一条直线
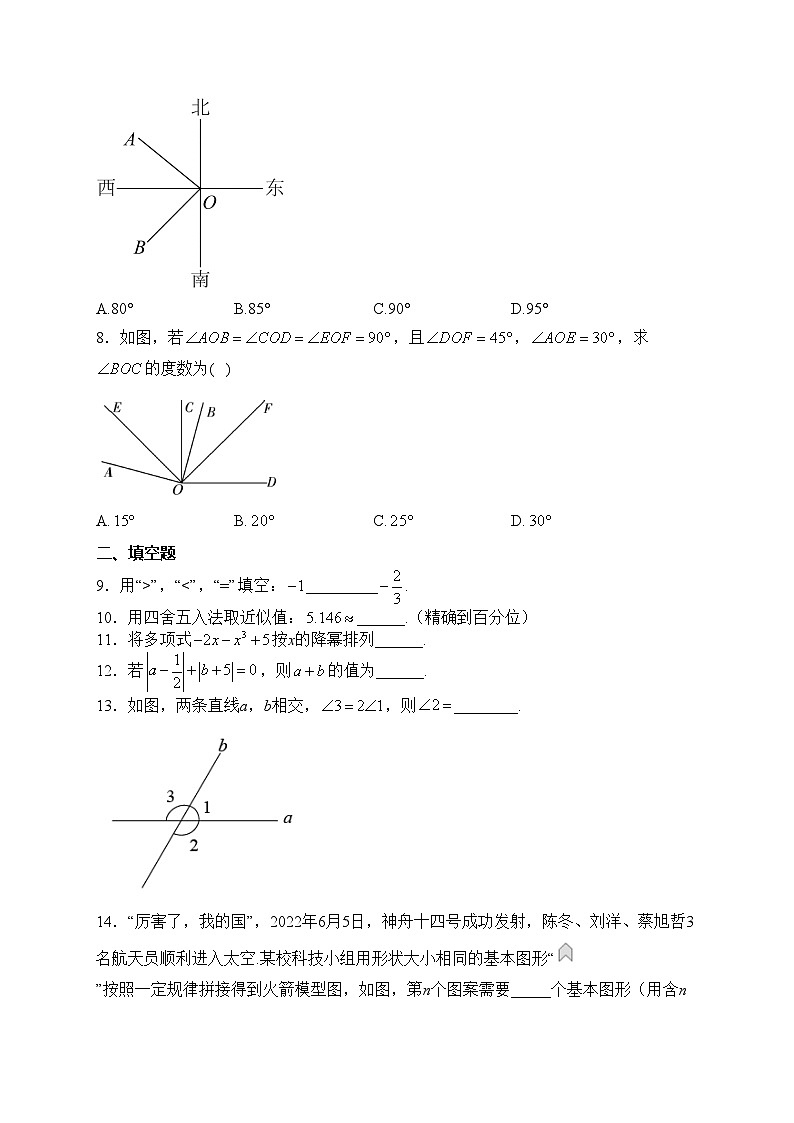
7．如图，在观测站O发现客轮A，货轮B分别在它北偏西50°，西南方向，则的度数是( )
A.80°B.85°C.90°D.95°
8．如图，若，且，，求的度数为( )
A.B.C.D.
二、填空题
9．用“>”，“<”，“=”填空：_________.
10．用四舍五入法取近似值：______.（精确到百分位）
11．将多项式按x的降幂排列______.
12．若，则的值为______.
13．如图，两条直线a，b相交，，则________.
14．“厉害了，我的国”，2022年6月5日，神舟十四号成功发射，陈冬、刘洋、蔡旭哲3名航天员顺利进入太空.某校科技小组用形状大小相同的基本图形“”按照一定规律拼接得到火箭模型图，如图，第n个图案需要_____个基本图形（用含n的代数式表示）.
三、解答题
15．画一条数轴，并在数轴上标出下列各数.
-3，，-1.5，0，+3.5，4
16．计算：.
17．先化简，再求值：，其中，.
18．如图，在无阴影的方格中选出两个画出阴影，使它们与图中四个有阴影的正方形一起可以构成正方体表面的不同展开图（填出两种互相不同的答案）
19．2021年9月28日，第十三届中国航展在广东珠海举行，中国空军航空大学“红鹰”飞行表演队在航展上表演特技飞行，如图所示，表演从空中某一位置开始，上升的高度记作正数，下降的高度记作负数，五次特技飞行高度记录如下：，，，，.（单位：千米）
（1）求飞机最后所在的位置比开始位置高还是低？高了或低了多少千米？
（2）若飞机平均上升1千米需消耗6升燃油，平均下降1千米需消耗4升燃油，则飞机在这5次特技飞行中，一共消耗多少升燃油？
20．我们知道，分类讨论思想在数学中是非常重要的数学思想.请同学们阅读下面试题并把解题过程补充完整：
已知若，，且，则求的值.
因为，.
所以，.
因为，
所以______.
所以当______，______，______；
当______，______，______.
21．如图，，.求证：.
证明：（已知）
________∥________( )
________( )
( )
________（等量代换）
( )
22．商店出售羽毛球拍和羽毛球，每副球拍定价300元，每盒羽毛球定价40元.为庆祝“国庆节”，商店开展促销活动，向客户提供两种优惠方案，方案一：所有商品9折优惠；方案二：每买1副球拍赠送1盒羽毛球.现某校羽毛球队需要购买20副球拍和x盒羽毛球（）.
（1）若该校按方案一购买，需付款_________元（用含x的代数式表示）.
若该校按方案二购买，需付款_________元（用含x的代数式表示）.
（2）若，两种方案中，通过计算说明选择按哪种方案购买较合算.
（3）当时，你能给出一种更为省钱的购买方案吗？试写出你的方案，并计算出所需的钱数.
23．教材呈现：下图是华师版七年级上册数学教材第176页的部分内容.
（1）小明根据提示，写出了如下证明过程.根据小明的推理过程，在括号内填写理由.
，
( ).
( )，
( ).
（2）如图①，.若，则的余角的大小为______度.
（3）如图②，，，若，求的大小.
24．如图，点在线段上，，，动点P从点A出发，沿线段以每秒3个单位长度的速度向终点B匀速运动；同时，动点Q从点B出发，沿线段以每秒2个单位长度的速度向终点A匀速运动.当点P到达终点时，点Q也随之停止运动.
设点P的运动时间为t秒.
（1）线段的长为______.
（2）当点P与点Q相遇时，求t的值.
（3）当点P与点Q之间的距离为9个单位长度时，求t的值.
（4）当时，直接写出t的值.
参考答案
1．答案：C
解析：的相反数是.
故选C.
2．答案：B
解析：；
故选：B.
3．答案：A
解析：单项式的系数是，
故选：A.
4．答案：A
解析：试题解析：比a的平方的2倍小1的数为：
故选A.
5．答案：B
解析：从前面看可得到从左到右第1列有1个正方形，第2列有个1正方形，第3列有个2正方形，
故选B.
6．答案：A
解析：弯曲的河道改直，根据的原理是：两点之间，线段最短，
A选项符合题意，B、C、D均不符合题意；
故选：A.
7．答案：B
解析：由题意得：，
故选：B.
8．答案：A
解析：，，
，
，
，
又，，
，
故选：A.
9．答案：<
解析：，，
，
.
故答案为：<.
10．答案：5.15
解析：用四舍五入法取近似值：；
故答案为：5.15.
11．答案：
解析：多项式的各项为：、、，
按x的降幂排列为.
故答案为：.
12．答案：
解析：，且，，
，，
，，
；
故答案为.
13．答案：
解析：，，
，，
，
，
故答案为：120°.
14．答案：
解析：第1个图案需要1个基本图形，，
第2个图案需要5个基本图形，，
第3个图案需要9个基本图形，，
第4个图案需要13个基本图形，，
第5个图案需要17个基本图形，，
第6个图案需要21个基本图形，，
……
第n个图案需要个基本图形，，
故答案：.
15．答案：见解析
解析：如图：
16．答案：
解析：
.
17．答案：，
解析：
，
当，时，
原式
.
18．答案：见解析
解析：如图所示，即为所求.
19．答案：（1）飞机最后所在的位置比开始位置高，高
（2）37.2升
解析：（1）由题意可知：五次特技飞行高度之和为：，
飞机最后所在的位置比开始位置高，高.
（2）飞机上升的高度为：，
飞机下降的高度为：
飞机平均上升1千米需消耗6升燃油，平均下降1千米需消耗4升燃油，
一共消耗燃油：升.
20．答案：；；5；3；；；
解析：因为，.
所以，.
因为，
所以.
所以当，，；
当，，.
21．答案：AD；BC；内错角相等，两直线平行；；两直线平行，同旁内角互补；已知；；同旁内角互补，两直线平行
解析：证明：（已知）
（内错角相等，两直线平行）
（两直线平行，同旁内角互补）
（已知）
（等量代换）
（同旁内角互补，两直线平行）.
22．答案：（1）；
（2）按方案二购买较合算
（3）能，按方案二购买20副球拍，按方案一购买10盒羽毛球；6360元
解析：（1）能.
按方案一购买，需付款元；
按方案二购买，需付款元；
故答案为：；；
（2）当时，（元），（元），
因，
故选择按方案二购买较合算.
（3）所有球拍全部按方案二购买，剩下的10盒羽毛球则按方案一购买，则需付款：（元）；
答：按方案二购买20副球拍，按方案一购买10盒羽毛球；需付款6360元.
23．答案：（1）两直线平行，同位角相等；对顶角相等；等量代换
（2）25
（3）47°
解析：（1），
（两直线平行，同位角相等）.
（对顶角相等），
（等量代换）.
故答案为：两直线平行，同位角相等；对顶角相等；等量代换；
（2），
，
，
，
余角的度数为：，
故答案为：25；
（3），
.
，
.
.
，
.
24．答案：（1）14
（2）
（3）当或时，点P与点Q之间的距离为9个单位长度
（4）
解析：（1）点C在线段上，，，
，
故答案为：14.
（2）依题意，，，
当点P与点Q相遇时，
解得：；
（3）相遇前点P与点Q之间的距离为9个单位长度时，
，
解得：，
相遇前点P与点Q之间的距离为9个单位长度时，则
，
解得：，
综上所述，当或时，点P与点Q之间的距离为9个单位长度；
（4），
当P在线段上时，，此时，
，
，
解得：（舍去）
当P在线段上时，，此时，
，
，
解得：，
.
有了“两直线平行，同位角相等”，我们就能用推理的方法得出“两条平行线被第三条直线所截，内错角相等”.
如图，平行线a、b被直线l所截，我们将的对顶角记为…