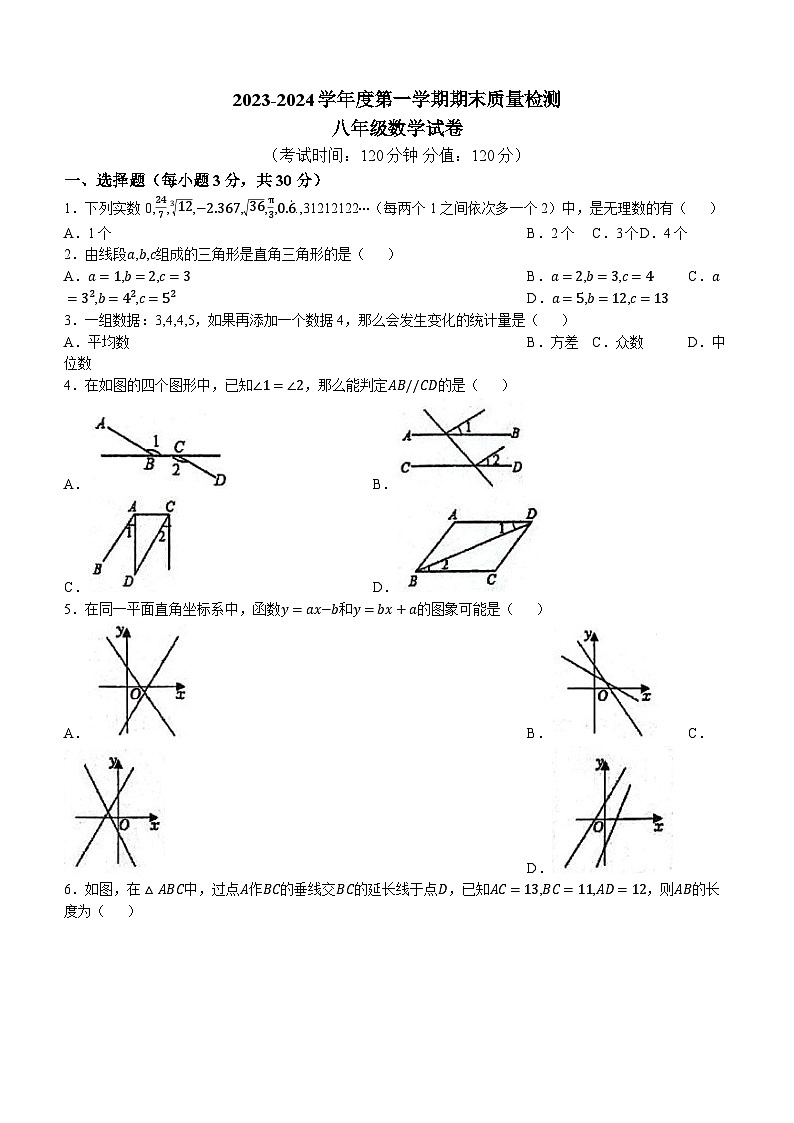
陕西省西安市第三中学名校2023-2024学年八年级上学期期末数学试题

这是一份陕西省西安市第三中学名校2023-2024学年八年级上学期期末数学试题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

（考试时间：120分钟 分值：120分）
一、选择题（每小题3分，共30分）
1．下列实数0,247,312,−2.367,36,π3,0.6.,31212122⋯（每两个1之间依次多一个2）中，是无理数的有（ ）
A．1个B．2个C．3个D．4个
2．由线段a,b,c组成的三角形是直角三角形的是（ ）
A．a=1,b=2,c=3B．a=2,b=3,c=4C．a=32,b=42,c=52D．a=5,b=12,c=13
3．一组数据：3,4,4,5，如果再添加一个数据4，那么会发生变化的统计量是（ ）
A．平均数B．方差C．众数D．中位数
4．在如图的四个图形中，已知∠1=∠2，那么能判定AB//CD的是（ ）
A．B．
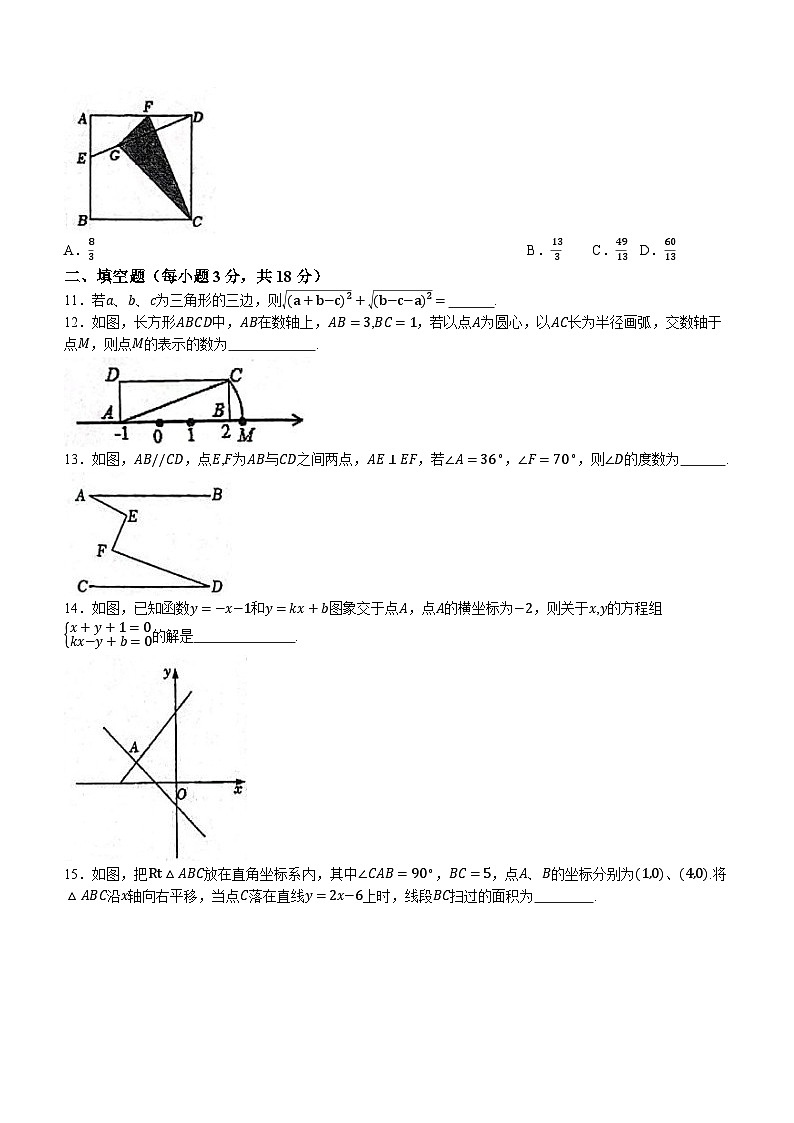
C．D．
5．在同一平面直角坐标系中，函数y=ax−b和y=bx+a的图象可能是（ ）
A．B．C．D．
6．如图，在△ABC中，过点A作BC的垂线交BC的延长线于点D，已知AC=13,BC=11,AD=12，则AB的长度为（ ）
A．15B．16C．18D．20
7．中国古代人民在生产生活中发现了许多数学问题，在《孙子算经》中记载了这样一个问题，大意为：有若干人乘车，若每车乘坐3人，则2辆车无人乘坐；若每车乘坐2人，则9人无车可乘，问共有多少辆车，多少人，设共有x辆车，y人，则可列方程组为（ ）
A．3x−2=y2x+9=yB．3x+2=y2x+9=yC．3x=y2x+9=yD．3x+2=y2x−9=y
8．如图，在等边三角形ABO中，边OA在x轴上，点A的坐标为−m,0，直线y=−32x+23于x轴交于点C，与y轴交于点D，将△ABO沿x轴向右平移3个单位，点B的对应点B′恰好落在直线CD上，则点B′的坐标为（ ）
A．2,3B．3,3C．2,23D．2,2
9．如图，已知△ABC中，AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E，点M,N为垂足，若BD=32,DE=2,EC=52，则AC的长为（ ）
A．322B．332C．352D．3102
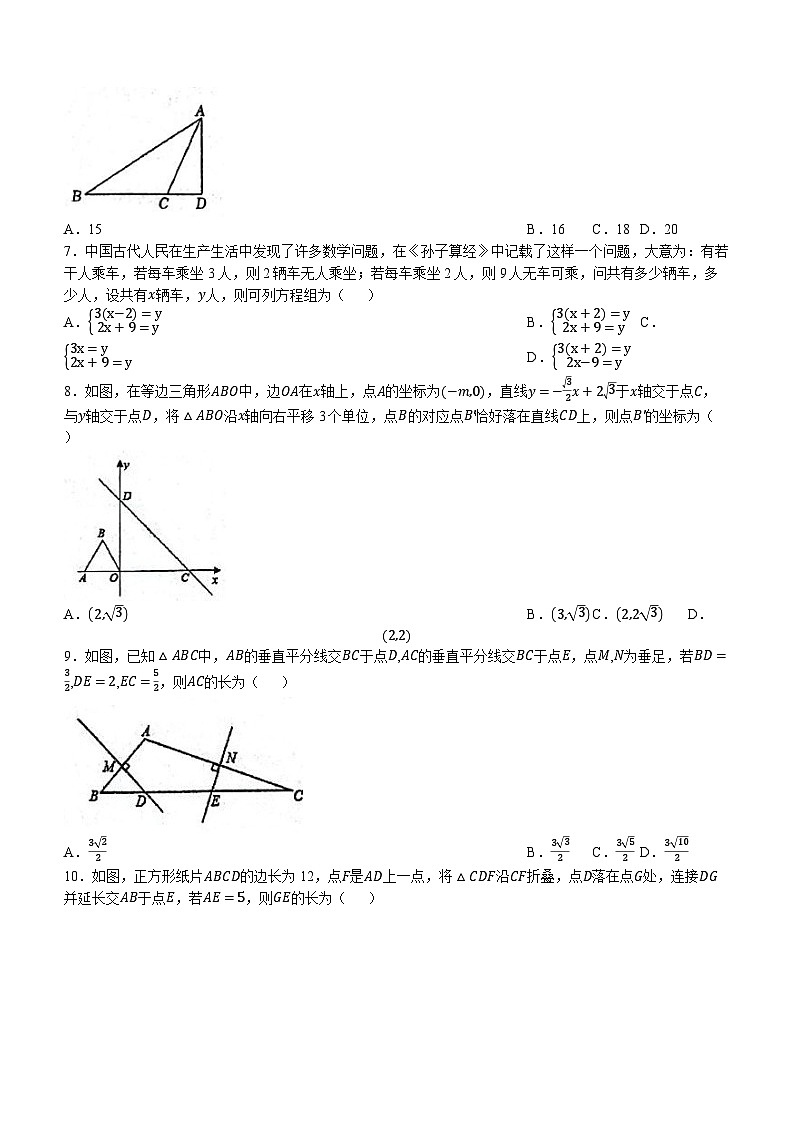
10．如图，正方形纸片ABCD的边长为12，点F是AD上一点，将△CDF沿CF折叠，点D落在点G处，连接DG并延长交AB于点E，若AE=5，则GE的长为（ ）
A．83B．133C．4913D．6013
二、填空题（每小题3分，共18分）
11．若a、b、c为三角形的三边，则a+b−c2+b−c−a2= .
12．如图，长方形ABCD中，AB在数轴上，AB=3,BC=1，若以点A为圆心，以AC长为半径画弧，交数轴于点M，则点M的表示的数为 .
13．如图，AB//CD，点E,F为AB与CD之间两点，AE⊥EF，若∠A=36∘，∠F=70∘，则∠D的度数为 .
14．如图，已知函数y=−x−1和y=kx+b图象交于点A，点A的横坐标为−2，则关于x,y的方程组x+y+1=0kx−y+b=0的解是 .
15．如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90∘，BC=5，点A、B的坐标分别为1,0、4,0.将△ABC沿x轴向右平移，当点C落在直线y=2x−6上时，线段BC扫过的面积为 .
16．如图，四边形ABCD,AD=1,AB=23，BC=3，点E为AB的中点，连接DE、CE，使得∠DEA+∠CEB=60∘，则DC的最大值为 .
三、解答题（共72分）
17．计算、解方程：（每小题4分，共16分）
（1）43−2021−π0+3−2
（2）−3+12−5+3×5−3
（3）2x+5y=13x−y=13
（4）3x−y=9x2−y3=2
18．（6分）如图，在平面直角坐标系中，已知A−2,−1,B−4,−3,C2,−2.
（1）作出△ABC关于x轴对称的△A′B′C′;
（2）求△A′B′C′的面积；
（3）若点P在x轴上，求PA+PC的最小值.
19．（6分）如图，在△ABC中，∠A=90∘，AB=AC,D为BC的中点，E,F分别是AB,AC上的点.且BE=AF.
（1）求证：ED=DF.
（2）若ED=2，求EF的长.
20．（6分）为积极落实“双减”政策，让作业布置更加精准高效，我校现对八年级部分学生每天完成作业所用的时间进行调查，并用得到的数据绘制了不完整的统计图，根据图中信息完成下列问题：
（1）本次共调查了 名学生，并补全条形统计图；
（2）本次抽查学生每天完成作业所用时间的中位数为 ；众数为 ；
（3）我校八年级有1200名学生，请你估计八年级学生中，每天完成作业所用时间为1.5小时的学生有多少人？
21．（6分）如图，某小区有两个喷泉A,B，两个喷泉的距离长为250m.现要为喷泉铺设供水管道AM，BM，供水点M在小路AC上，供水点M到AB的距离MN的长为120m,BM的长为150m.
（1）求供水点M到喷泉A,B需要铺设的管道总长；
（2）求喷泉B到小路AC的最短距离.
22．（6分）我校将举办一年一度的秋季运动会，需要采购一批某品牌的乒乓球拍和配套的乒乓球，一副球拍标价80元，一盒球标价25元.体育商店提供了两种优惠方案，具体如下：
方案甲：买一副乒乓球拍送一盒乒乓球，其余乒乓球按原价出售；
方案乙：按购买金额打9折付款.
学校欲购买这种乒乓球拍10副，乒乓球xx≥10盒.
（1）请直接写出两种优惠办法实际付款金额y甲（元），y乙（元）与x（盒）之间的函数关系式.
（2）如果学校需要购买15盒乒乓球，哪种优惠方案更省钱？
（3）如果学校提供经费为1800元，选择哪个方案能购买更多乒乓球？
23．（6分）用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法，请你用等面积法来探究下列三个问题：
（1）如图1是著名的“赵爽弦图”，由四个全等的直角三角形拼成，请用它验证勾股定理c2=a2+b2.
（2）如图2，在Rt△ABC中，∠ACB=90∘，CD是AB边上的高，AC=4，BC=3，求CD的长度；
（3）如图1，若大正方形的面积是13，小正方形的面积是1，求a+b2的值a24．（8分）已知用2辆A型车和1辆B型车装满货物一次可运货10吨；用1辆A型车和2辆B型车装满货物一次可运货11吨，某物流公司现有31吨货物，计划同时租用A型车m辆，B型车n辆，一次运完，且恰好每辆车都装满货物.
根据以上信息，解答下列问题：
（1）一辆A型车和一辆B型车装满货物一次可分别运货多少吨？
（2）请你帮物流公司设计出所有可行的租车方案.
（3）若A型车每辆租金100元/次，B型车每辆租金120元/次，请选出最省钱的租车方案，并求出最少租金费.
25．（12分）
（1）模型建立：
如图1，在等腰直角三角形ABC中，∠ACB=90∘，CA=CB，直线ED经过点C，过点A作AD⊥ED于点D,过点B作BE⊥ED于点E，请直接写出图中相等的线段（除CA=CB）;
模型应用：
（2）如图2，在平面直角坐标系xOy中，直线y=43x+8与x,y轴分别交于A、B两点，C为第一象限内的点，若△ABC是以AB为直角边的等腰直角三角形，请求出点C的坐标和直线BC的表达式；
探究提升：
（3）如图3，在平面直角坐标系xOy中，A3,0，点B在y轴上运动，将AB绕点A顺时针旋转90∘至AC，连接OC，求CA+OC的最小值，及此时点B坐标.
【参考答案】
2023-2024学年度第一学期期末质量检测
八年级数学试卷
一、选择题（每小题3分，共30分）
1．C 2．D 3．B 4．A 5．D 6．D 7．A 8．A 9．D 10．C
二、填空题（每小题3分，共18分）
11．2a
12．10−1
13．16∘
14．x=−2y=1
15．16
16．4+3
三、解答题（共72分）
17．（1） 1−33
（2） −23
（3） {x=2y=−1
（4） {x=2y=−3
18．（1）
解：如图，△A′B′C′即为所求；
（2） △A′B′C′的面积为6×2−12×2×2−12×4×1−12×6×1=5；
（3）
如图，连接A′C，与x轴的交点即为所求的点P,
∴PA+PC的最小值即为A′C的长，
由勾股定理得A′C=32+42=5,
∴PA+PC的最小值为5.
19．（1）
证明：如图，连接AD,
∵AB=AC,∠BAC=90∘，D为BC中点，
∴AD=12BC=BD=CD，且AD平分∠BAC,
∴∠BAD=∠CAD=45∘，
在△BDE和△ADF中，
BD=AD∠B=∠DAF=45∘BE=AF，
∴△BDE≅△ADFSAS,
∴DE=DF;
（2）
解：∵△BDE≅△ADF,
∴DE=DF,∠BDE=∠ADF,
∵∠BDE+∠ADE=90∘，
∴∠ADF+∠ADE=90∘，
∴∠EDF=90∘，
∴△EDF为等腰直角三角形.
∴EF=2DE=22.
20．（1）
100； 补全的条形统计图如图所示：
解：本次调查的人数为：30÷30%=100（人），
完成作业时间为1.5小时的有：100−12−30−18=40（人），
（2） 1.5小时； 1.5小时
【解析】由（1）中的条形统计图可知，抽查学生完成作业所用时间的众数是1.5小时，
∵100÷2=50，则中位数是1.5小时，
故答案为：1.5小时，1.5小时；
（3）
40÷100=40%，1200×40%=480（人），
答：八年级学生中，每天完成作业所用时间为1.5小时的学生有480人.
21．（1）
解：在Rt△MNB中，BN=BM2−MN2=1502−1202=90m,
∴AN=AB−BN=250−90=160m,
在Rt△AMN中，AM=AN2+MN2=1602+1202=200m,
∴供水点M到喷泉A,B需要铺设的管道总长=200+150=350m;
（2）
∵AB=250m,AM=200m,BM=150m,
∴AB2=BM2+AM2,
∴△ABM是直角三角形，
∴BM⊥AC,
∴喷泉B到小路AC的最短距离是BM=150m.
22．（1）
解：由题意得：
y甲=10×80+25x−10=25x+550,
yz=25×0.9x+80×0.9×10=22.5x+720,
（2）
根据（1）中解析式，y甲=25x+550,y乙=22.5x+720,
当x=15时y甲=25×15+550=925（元），
y乙=22.5×15+720=1057.5（元），
∵925<1057.5,
∴方案甲更省钱；
（3）
根据（1）中解析式，y甲=25x+550,yz=22.5x+720,
当y甲=1800元时，1800=25x+550，解得：x=50,
当y乙=1800元时，1800=22.5x+720，解得：x=48,
∵50>48,
∴学校提供经费为1800元，选择方案甲能购买更多乒乓球.
23．（1）
解：如图1，大正方形的面积=c2=4×12ab+b−a2,
整理得，c2=a2+b2;
（2）
在Rt△ABC中，∠ACB=90∘，AC=4,BC=3,
∴AB=32+42=5，
∵S△ABC=12AC⋅BC=12AB⋅CD,
∴CD=AC⋅BCAB=125；
（3）
∵大正方形的面积是13，小正方形的面积是1，
∴c2=13,b−a2=1, ∴a2+b2−2ab=1,
∴2ab=12,
∴a+b2=a2+b2+2ab=13+12=25,
即a+b2的值为25.
24．（1）
解：设一辆A型车装满货物可运货x吨，一辆B型车装满货物可运货y吨，
根据题意，得：2x+y=10x+2y=11，解得：x=3y=4，
答：一辆A型车装满货物可运货3吨，一辆B型车装满货物可运货4吨；
（2）
由题意得：3m+4n=31,
∵m、n均为正整数，
∴m=1n=7或m=5n=4或m=9n=1，
∴该物流公司共有以下三种租车方案，
方案一：租A型车1辆，B型车7辆；
方案二：租A型车5辆，B型车4辆；
方案三：租A型车9辆，B型车1辆.
（3）
方案一费用：100×1+120×7=940（元），
方案二费用：100×5+120×4=980（元），
方案三费用：100×9+120×1=1020（元），
∵940<980<1020,∴方案一：租A型车1辆，B型车7辆，最省钱，最少租车费为940元.
25．（1）
解：∵∠ACB=90∘，
∴∠ACD+∠BCE=90∘.
∵AD⊥ED，BE⊥ED,
∴∠D=∠E=90∘，
∴∠ACD+∠CAD=90∘，
∴∠CAD=∠BCE,
∵CA=CB,
∴△ACD≅△CBEAAS,
∴AD=CE,CD=BE.
（2）
以点A为直角顶点时，如图，作CD⊥OA于点D.
∵y=43x+8
∴x=0时，y=8；当y=0时，x=6,
∴A6,0,B0,8.
∵∠CAB=90∘，
∴∠CAD+∠BAO=90∘.
∵CD⊥OA,
∴∠AOB=∠ADC=90∘，
∴∠ACD+∠CAD=90∘，
∴∠ACD=∠BAO,
∵CA=AB,
∴△ACD≅△BAOAAS,
∴AD=OB=8,CD=OA=6,
∴OD=6+8=14,
∴C14,6. 设直线BC的解析式为y=kx+8，把C14,6代入，得14k+8=6,
∴k=−17.
∴y=17x+8:
当以点B为直角顶点时，作CD⊥OB于点D.如图，
同理可求：CD=OB=8,BD=OA=6,
∴OD=6+8=14,
∴C8,14.
设直线BC的解析式为y=nx+8，把C8,14代入，得8n+8=14,
∴k=34
∴y=34x+8
（3）
如图，过点C作CD⊥OA轴于点D，设OB=t.
∵∠CAB=90∘，
∴∠CAD+∠BAO=90∘，
∵CD⊥OA,
∴∠AOB=∠ADC=90∘，
∴∠ACD+∠CAD=90∘，
∴∠ACD=∠BAO,
∵CA=AB,
∴△ACD≅△BAOAAS,
∴AD=OB=t,CD=OA=3,
∴OD=t−3,
∴C3−t,3,
∴CA+OC=t2+32+t−32+32,
设Pt,0,M0,3,N3,3,
则求t2+32+t−32+32的最小值可看作点P到点M和点N的距离之和最小，如图，
作点M0,3关于x轴的对称点M′0,−3，连接M′N交x轴于点P，连接MP,
则PM+PN=PM′+PN=M′N=32+3+32=35.
设直线M′N的解析式为y=mx−3，把N3,3代入得3m−3=3,
∴m=2,
∴y=2x−3,
当y=0时，x=32，
∴P32,0,
∴此时t=32，
∴B0,32.