陕西省兴平市初级中学2023-2024学年数学九年级第一学期期末联考试题含答案

这是一份陕西省兴平市初级中学2023-2024学年数学九年级第一学期期末联考试题含答案，共8页。试卷主要包含了如图，在中，，则的值为，如图所示的几何体的主视图为等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题(每小题3分,共30分)
1．如果将抛物线向右平移1个单位，那么所得新抛物线的顶点坐标是（ ）
A．B．C．D．
2．如图，四边形ABCD是⊙O的内接四边形，若∠A=70°，则∠C的度数是（ ）
A．100°B．110°C．120°D．130°
3．如图，该几何体的主视图是( )
A．B．C．D．
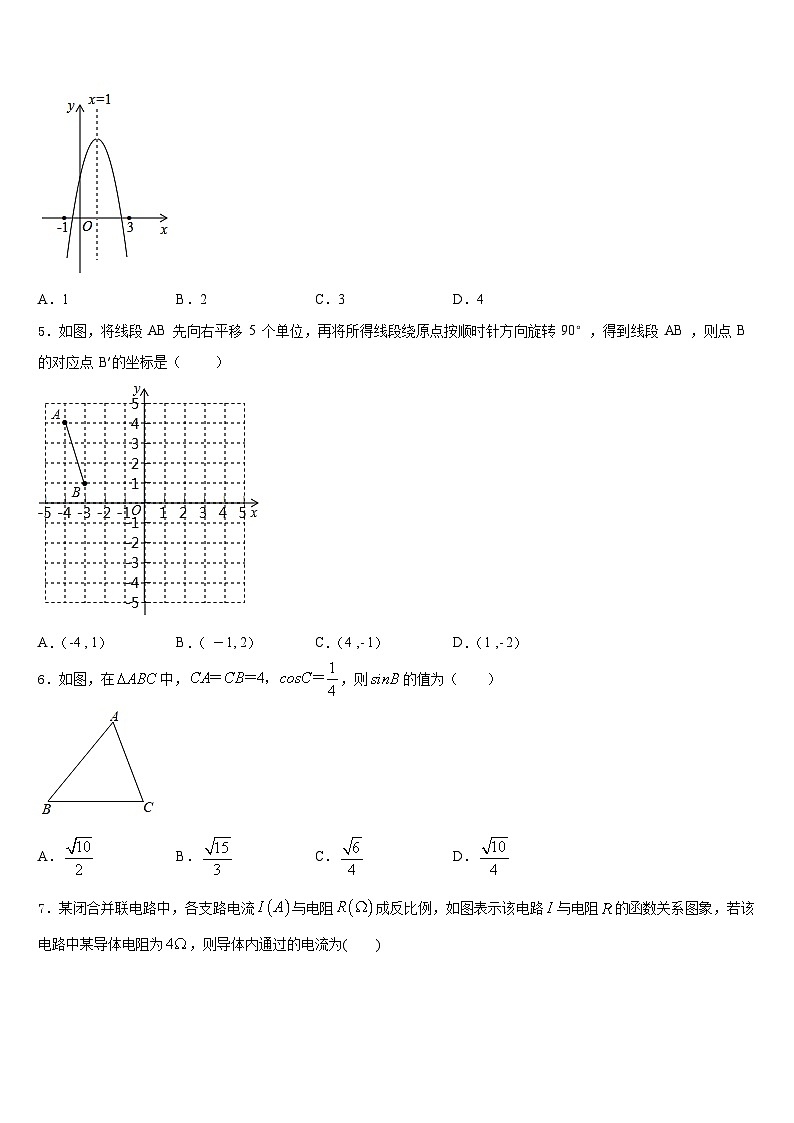
4．二次函数图象如图，下列结论：①；②；③当时，；④；⑤若，且，．其中正确的结论的个数有（ ）
A．1B．2C．3D．4
5．如图，将线段 AB 先向右平移 5 个单位，再将所得线段绕原点按顺时针方向旋转 90°，得到线段 AB ，则点 B 的对应点 B′的坐标是（ ）
A．（-4 , 1）B．（ －1, 2）C．（4 ,- 1）D．（1 ,- 2）
6．如图，在中，，则的值为（ ）
A．B．C．D．
7．某闭合并联电路中，各支路电流与电阻成反比例，如图表示该电路与电阻的函数关系图象，若该电路中某导体电阻为，则导体内通过的电流为( )
A．B．C．D．
8．如图是一根电线杆在一天中不同时刻的影长图，试按其天中发生的先后顺序排列，正确的是（ ）
A．①②③④B．④①③②C．④②③①D．④③②①
9．方程x2﹣2x+3=0的根的情况是（ ）
A．有两个相等的实数根B．只有一个实数根
C．没有实数根D．有两个不相等的实数根
10．如图所示的几何体的主视图为( )
A．B．C．D．
二、填空题(每小题3分,共24分)
11．如图，点A是反比例函数y=（x＞0）图象上一点，直线y=kx+b过点A并且与两坐标轴分别交于点B，C，过点A作AD⊥x轴，垂足为D，连接DC，若△BOC的面积是4，则△DOC的面积是______．
12．如图，在平面直角坐标系中，直线l的函数表达式为y＝x，点O1的坐标为（1，0），以O1为圆心，O1O为半径画圆，交直线l于点P1，交x轴正半轴于点O2，以O2为圆心，O2O为半径画圆，交直线l于点P2，交x轴正半轴于点O3，以O3为圆心，O3O为半径画圆，交直线l于点P3，交x轴正半轴于点O4；…按此做法进行下去，其中的长为_____．
13．如图，一个小球由地面沿着坡度i＝1：2的坡面向上前进了10m，此时小球距离出发点的水平距离为__m．
14．在本赛季比赛中，某运动员最后六场的得分情况如下：则这组数据的极差为_______．
15．如图，已知等边的边长为，，分别为，上的两个动点，且，连接，交于点，则的最小值_______．
16．反比例函数图像经过点（2，－3），则它的函数表达式是 ．
17．一个不透明的盒子中有4个白球，3个黑球，2个红球，各球的大小与质地都相同，现随机从盒子中摸出一个球，摸到白球的概率是_____．
18．如图，在平面直角坐标系中，正方形OABC与正方形ODEF是位似图形，点O为位似中心，位似比为2：3，点B、E在第一象限，若点A的坐标为（4，0），则点E的坐标是_____．
三、解答题(共66分)
19．（10分）如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA
与⊙O的另一个交点为E，连结AC，CE．
（1）求证：∠B=∠D；
（2）若AB=4，BC-AC=2，求CE的长．
20．（6分）解方程：x（x﹣3）+6＝2x．
21．（6分）甲、乙两名同学5次数学练习（满分120分）的成绩如下表：（单位：分）
已知甲同学这5次数学练习成绩的平均数为100分，方差为10分.
（1）乙同学这5次数学练习成绩的平均数为 分，方差为 分；
（2）甲、乙都认为自已在这5次练习中的表现比对方更出色，请你分别写出一条支持他们俩观点的理由.
22．（8分）如图，已知中，，是的中点，．
求证：四边形是菱形．
23．（8分）在边长为1个单位长度的正方形网格中，建立如图所示的平面直角坐标系，的顶点都在格点上，请解答下列问题：
(1)作出向左平移4个单位长度后得到的，并写出点的坐标；
(2)作出关于原点Ｏ对称的，并写出点的坐标；
(3)已知关于直线L对称的的顶点的坐标为(-4，-2)，请直接写出直线L的函数解析式．
24．（8分）京杭大运河是世界文化遗产．综合实践活动小组为了测出某段运河的河宽（岸沿是平行的），如图，在岸边分别选定了点A、B和点C、D，先用卷尺量得AB=160m，CD=40m，再用测角仪测得∠CAB=30°，∠DBA=60°，求该段运河的河宽（即CH的长）．
25．（10分）某企业生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD、线段CD分别表示该产品每千克生产成本（单位：元）、销售价（单位：元）与产量x（单位：kg）之间的函数关系．
（1）请解释图中点D的横坐标、纵坐标的实际意义；
（2）求线段AB所表示的与x之间的函数表达式；
（3）当该产品产量为多少时，获得的利润最大？最大利润是多少？
26．（10分）如图，点为上一点，点在直径的延长线上，且，过点作的切线，交的延长线于点.
判断直线与的位置关系，并说明理由；
若，求:①的半径，②的长.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、D
4、C
5、D
6、D
7、B
8、B
9、C
10、B
二、填空题(每小题3分,共24分)
11、1﹣1．
12、22015π
13、．
14、1
15、
16、．
17、．
18、（6，6）．
三、解答题(共66分)
19、（1）见解析（2）
20、x1＝2，x2＝1．
21、（1）100，10；（2）答案不唯一，如：甲的数学成绩逐渐进步，更有潜力；
乙的数学成绩在100分以上（含100分）的次数更多.
22、详见解析．
23、（1）图详见解析，C1（-1，2）； （2）图详见解析，C2（-3，-2）；（3）
24、该段运河的河宽为．
25、（1）点D的横坐标、纵坐标的实际意义：当产量为130kg时，该产品每千克生产成本与销售价相等，都为42元；（2）y=﹣0.2x+60（0≤x≤90）；（3）当该产品产量为75kg时，获得的利润最大，最大值为1．
26、 (1) 直线与相切；见解析（2）①3；②6.
测试日期
11月5日
11月20日
12月5日
12月20日
1月3日
甲
96
97
100
103
104
乙
100
95
100
105
100