贵州省贵阳市2024年中考模拟数学考试试卷附答案

这是一份贵州省贵阳市2024年中考模拟数学考试试卷附答案，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．计算的结果为（ ）
A．B．C．D．
2．如图，将矩形绕着它的一边所在的直线旋转一周，可以得到的立体图形是（ ）
A．B．C．D．
3．年“五一”假期期间，贵阳贵安旅游市场在贵阳市文旅系统精心策划下强势复苏，游客出行热情高涨，累计接待旅游者约人次，这个数用科学记数法可表示为（ ）
A．B．C．D．
4．如图，直线，被直线所截，，，则的度数为（ ）
A．B．C．D．
5．在平面直角坐标系中，下列各点在轴上的是（ ）
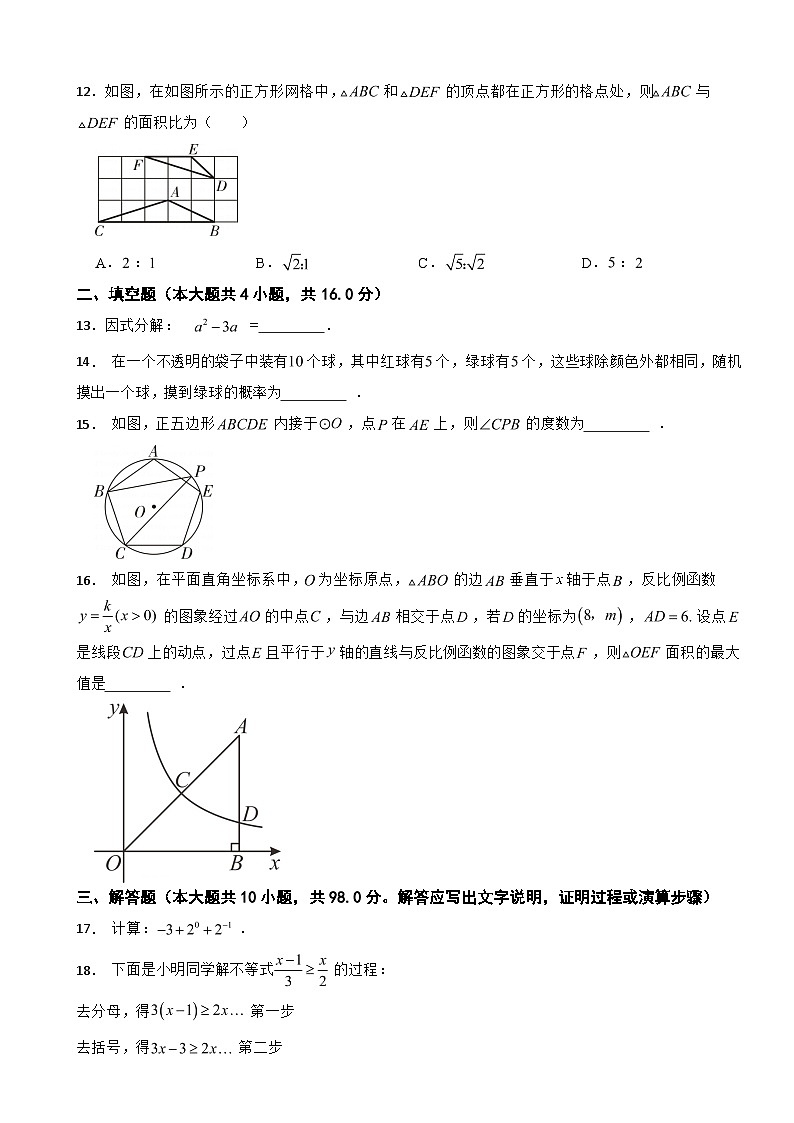
A．B．C．D．
6．如果将分式中的和都扩大倍，那么分式的值（ ）
A．不变B．扩大倍C．缩小倍D．扩大倍
7．校运会米短跑项目预赛中，名运动员的成绩各不相同，取前名参加决赛，其中运动员小军已经知道自己的成绩，他想确定自己是否进入决赛，需要知道这名运动员成绩的（ ）
A．方差B．众数C．平均数D．中位数
8．如图，在矩形中，对角线与相交于点，若，则的长度是（ ）
A．B．C．D．
9．骆驼被称为“沙漠之舟”，它的体温随时间的变化而发生较大的变化如图反映了骆驼的体温随时间的变化情况，下列说法错误的是（ ）
A．骆驼体温从最低上升到最高需要小时
B．骆驼体温一天内有两次达到
C．从时到时，骆驼的体温逐渐上升
D．第一天时与第二天时，骆驼的体温相同
10．如图，中，，以点为圆心，适当长为半径画弧，分别交，于点，，再分别以点，为圆心，大于的长为半径画弧，两弧交于点，作射线交于点若，则点到的距离为（ ）
A．B．C．D．
11．九章算术中记载了一个问题，大意是：有几个人一起去买一件物品，每人出元，多元；每人出元，少元问有多少人？小红是这样想的：设有人，物品价值元，她先列了一个方程，请你帮她再列出另一个方程（ ）
A．B．C．D．
12．如图，在如图所示的正方形网格中，和的顶点都在正方形的格点处，则与的面积比为（ ）
A．：B．C．D．：
二、填空题（本大题共4小题，共16.0分）
13．因式分解： = ．
14． 在一个不透明的袋子中装有个球，其中红球有个，绿球有个，这些球除颜色外都相同，随机摸出一个球，摸到绿球的概率为 ．
15． 如图，正五边形内接于，点在上，则的度数为 ．
16． 如图，在平面直角坐标系中，为坐标原点，的边垂直于轴于点，反比例函数的图象经过的中点，与边相交于点，若的坐标为，设点是线段上的动点，过点且平行于轴的直线与反比例函数的图象交于点，则面积的最大值是 ．
三、解答题（本大题共10小题，共98.0分。解答应写出文字说明，证明过程或演算步骤）
17． 计算：．
18． 下面是小明同学解不等式的过程：
去分母，得第一步
去括号，得第二步
移项、合并同类项，得第三步
小明的解答过程从第 步开始出现错误，请写出你认为正确的解答过程．
19．某学校为了解九年级学生体育训练情况，对九年级学生进行了一次体育模拟测试测试
结束后，随机抽取了班和班各名学生的测试成绩进行整理分析：
抽取的班学生的测试成绩单位：分如下：，，，，，，，，，，，，，，，，，，，
抽取的班学生成绩单位：分用表示，整理后分成如下五组：组：；组：：组：；组：；组：并绘制成如图所示扇形统计图，其中组学生的成绩为：，，，，，
抽取班与班学生测试成绩的平均数、中位数、众数如表所示：
（1）根据上述信息可得： ， ， ；
（2）结合以上数据分析，你认为哪个班学生的体育成绩更好？请说明理由．
20．如图，在四边形中，，，对角线，交于点，平分．
（1）求证：四边形是菱形；
（2）如图，过点作交的延长线于点，连接若，，求的长．
21． 某校组织七年级学生赴社会实践基地开展课外社会实践活动，现有甲、乙两种客车可租，已知每辆甲种客车的租金比每辆乙种客车的租金多元，并且用元租甲种客车的辆数和用元租乙种客车的辆数相等．
（1）每辆甲种客车和每辆乙种客车的租金分别是多少元？
（2）该校七年级师生共人，计划租用甲、乙两种客车共辆已知甲种客车每辆载客人，乙种客车每辆载客人，则租车所需费用最少为多少元？
22． 如图，图是一辆登高云梯消防车的实物图，图是其工作示意图，起重臂是可伸缩的，且起重臂可绕点在一定范围内转动，张角为，转动点距离地面的高度为．
（1）当起重臂长度为，张角为时，求云梯消防车最高点距离地面的高度；
（2）某日，一居民家突发险情，该居民家距离地面的高度为，请问该消防车能否实施有效救援？参考数据：，，
23． 如图，一次函数的图象与轴，轴分别相交于，两点，与反比例函数的图象相交于点．
（1）求反比例函数的表达式；
（2）若点的横坐标为，过点作轴的平行线，交反比例函数的图象于点，连接求的面积．
24． 如图，是的直径，是上一点，于点，过点作的切线，交的延长线于点，连接．
（1）求证：是的切线；
（2）设交于点，若，，求的半径；
（3）在的条件下，求阴影部分的面积．
25． 在平面直角坐标系中，抛物线的对称轴是直线．
（1）求抛物线的表达式；
（2）点在抛物线上，若，请求出的取值范围；
（3）设点为抛物线上的一个动点，当时，点关于轴的对称点都在直线的上方，求的取值范围．
26．
（1）【阅读理解】如图，在中，，是斜边上的中线试判断与的数量关系解决此问题可以用如下方法：延长至点，使，连接，易证四边形是矩形，得到，即可作出判断则与的数量关系为 ；
（2）【问题探究】如图，直角三角形纸片中，，点是边的中点，连接，将沿折叠，点落在点处，此时恰好有若，求的长度；
（3）【拓展延伸】如图，在等腰直角三角形中，，，是边的中点，，分别是边，上的动点，且，当点从点运动到点时，的中点所经过的路径长是多少？
1．B
2．A
3．D
4．A
5．B
6．A
7．D
8．D
9．C
10．B
11．C
12．D
13．
14．
15．
16．1
17．解：原式
．
18．解：一小明的解答过程从第一步开始出现错误；正确的解答过程为：去分母得：，去括号得：，移项得：，合并得：，系数化为得：，所以原不等式的解集为：．
19．（1）；；
（2）解：根据以上数据，班学生的体育成绩更好，
理由：两个年级的平均成绩一样，而班的中位数、众数均高于班，说明就班学生的体育成绩更好．
20．（1）证明：，
，
平分，
，
，
，
，
，
，
四边形ABCD是平行四边形，
，
平行四边形ABCD是菱形；
（2）解：在菱形ABCD中，，，，
，
，
，
，
在中，，
．
21．（1）解：设每辆甲种客车的租金是元，则每辆乙种客车的租金是元，
由题意得：，
解得：，
经检验，是原方程的解，且符合题意，
，
答：每辆甲种客车的租金是元，每辆乙种客车的租金是元；
（2）解：设租用甲种客车辆，则租用乙种客车辆，
由题意得：，
解得：，
又、均为正整数，
可以为，，
共有种租车方案，
租用辆甲种客车，辆乙种客车，所需租车费用为元；
租用辆甲种客车，辆乙种客车，所需租车费用为元；
，
租车所需费用最少为元．
答：租车所需费用最少为元．
22．（1）解：如图，作于点，
，
四边形为矩形，
，，
，
在中，，
，
；
（2）解：如图，作于点，
，
四边形为矩形，
，，
，
在中，，
，
；
最高救援高度为，
故该消防车不能实施有效救援．
23．（1）解：将代入得，
点坐标为．
点在反比例函数的图象上，
．
反比例函数的表达式为：；
（2）解：将代入一次函数得，
即点的坐标为，
即点坐标为，
．
．
24．（1）证明：连接，如图，
为切线，
，
，
，
，
即垂直平分，
，
在和中，
，
≌，
，
半径，
与相切；
（2）解：，
，
，
，
，
的半径长为；
（3）解：，，
，
，
．
25．（1）解：抛物线的对称轴为，
．
解得：．
抛物线的解析式为．
（2）解：将代入抛物线的解析式得．
将代入得：．
解得：，．
，
当或时，．
（3）解：设点关于轴对称点为，则点运动的轨迹如图所示：
当时，．
点关于轴的对称点的坐标为．
当时，，
点关于轴的对称点的坐标为．
当时，
点关于轴的对称点都在直线的上方，
．
解得：．
当时，
点关于轴的对称点都在直线的上方，
．
解得；．
的取值范围是．
26．（1）
（2）解：如图中，设交于点．
，，
，
，
由翻折的性质可知，
，
，
，
，
，
，
，，
，
，
，
；
（3）解：过点作，，如图，
，，
．
是边中点，
，
同理：，
，
．
四边形为正方形，
．
，
，
．
．
在和中，
，
≌．
．
为等腰直角三角形，
当点从点运动到点时，的中点所经过的路径为，中点的连线，
即所经过的路径为，
，，
，
的中点所经过的路径长为．班级
平均数
中位数
众数
班
班